10.11 Quicksort

Sắp xếp nhanh là một ví dụ về thuật toán divide-and-conquer(chia để trị). Nó còn được gọi là sắp xếp trao đổi phân vùng. Nó sử dụng các lệnh gọi đệ quy để sắp xếp các phần tử và nó là một trong những thuật toán nổi tiếng trong số các thuật toán sắp xếp dựa trên so sánh.

Divide: Mảng $A[low ...high]$ được chia thành hai mảng con không trống $A[low ...q]$ và $A[q + 1... high]$, sao cho mỗi phần tử của $A[low ... high]$ nhỏ hơn hoặc bằng mỗi phần tử của $A[q + 1... high]$. Chỉ số q được tính như một phần của quy trình phân vùng này.

Conquer: Hai mảng con $A[low ...q]$ và $A[q + 1 ...high]$ được sắp xếp bằng cách gọi đệ quy Quick Sort.

Algorithm

Thuật toán đệ quy bao gồm bốn bước:

1. Nếu có một hoặc không có phần tử nào trong mảng được sắp xếp, hãy trả về.
2. Chọn một phần tử trong mảng để làm điểm “trục”. (Thông thường phần tử ngoài cùng bên trái hoặc phải của mảng được sử dụng.)
3. Chia mảng thành hai phần – một phần có các phần tử lớn hơn trục và phần còn lại có các phần tử nhỏ hơn trục.
4. Lặp lại đệ quy thuật toán cho cả hai nửa của mảng ban đầu.

Code mình có tham khảo ở đây

class GFG {
 
    // A utility function to swap two elements
    static void swap(int[] arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
 
    /* This function takes last element as pivot, places
       the pivot element at its correct position in sorted
       array, and places all smaller (smaller than pivot)
       to left of pivot and all greater elements to right
       of pivot */
    static int partition(int[] arr, int low, int high)
    {
 
        // pivot
        int pivot = arr[high];
 
        // Index of smaller element and
        // indicates the right position
        // of pivot found so far
        int i = (low - 1);
 
        for (int j = low; j <= high - 1; j++) {
 
            // If current element is smaller
            // than the pivot
            if (arr[j] < pivot) {
 
                // Increment index of
                // smaller element
                i++;
                swap(arr, i, j);
            }
        }
        swap(arr, i + 1, high);
        return (i + 1);
    }
 
    /* The main function that implements QuickSort
              arr[] --> Array to be sorted,
              low --> Starting index,
              high --> Ending index
     */
    static void quickSort(int[] arr, int low, int high)
    {
        if (low < high) {
 
            // pi is partitioning index, arr[p]
            // is now at right place
            int pi = partition(arr, low, high);
 
            // Separately sort elements before
            // partition and after partition
            quickSort(arr, low, pi - 1);
            quickSort(arr, pi + 1, high);
        }
    }
 
    // Function to print an array
    static void printArray(int[] arr, int size)
    {
        for (int i = 0; i < size; i++)
            System.out.print(arr[i] + " ");
 
        System.out.println();
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int[] arr = { 10, 7, 8, 9, 1, 5 };
        int n = arr.length;
 
        quickSort(arr, 0, n - 1);
        System.out.println("Sorted array: ");
        printArray(arr, n);
    }
}

Phân tích

Chúng ta hãy giả sử rằng T(n) là độ phức tạp của Quick Sort và cũng giả sử rằng tất cả các phần tử là khác nhau. Sự lặp lại của T(n) phụ thuộc vào hai kích thước bài toán con phụ thuộc vào phần tử phân vùng. Nếu trục là phần tử nhỏ thứ i thì chính xác (i – 1) mục sẽ ở phần bên trái và (n – i) ở phần bên phải. Hãy gọi nó là i –split. Vì mỗi phần tử có xác suất chọn nó làm trục như nhau nên xác suất chọn phần tử thứ i là $1/n$.

Best Case: Mỗi phân vùng chia mảng thành hai nửa và cho
$T(n) = 2T(n/2) + Θ(n) = Θ(nlogn)$ [Sử dụng Divide and Conquer master theorem ]

Worst Case: Mỗi phân vùng cho sự phân chia không cân bằng và chúng ta nhận được
$T(n) = T(n – 1) + Θ(n) = Θ(n2)$ [Sử dung using Subtraction and Conquer master theorem]

Trường hợp xấu nhất xảy ra khi danh sách đã được sắp xếp và phần tử cuối cùng được chọn làm trục.

Average Case: Trong trường hợp trung bình của Sắp xếp nhanh, chúng ta không biết nơi xảy ra sự phân tách. Vì lý do này, chúng ta lấy tất cả các giá trị có thể có của các vị trí được phân tách, cộng tất cả độ phức tạp của chúng và chia cho n để có được độ phức tạp trường hợp trung bình.

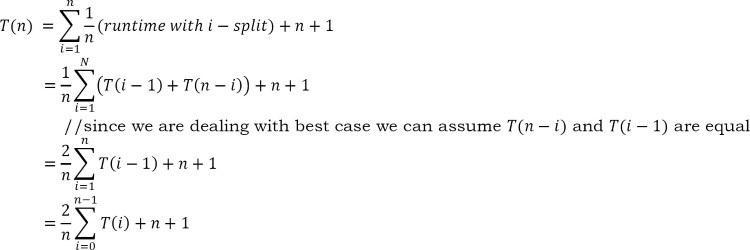
Nhân cả hai vế với n. (1)

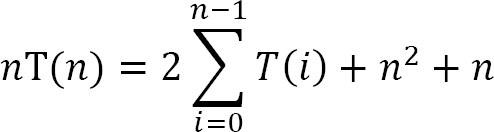
Công thức tương tự cho n – 1. (2)

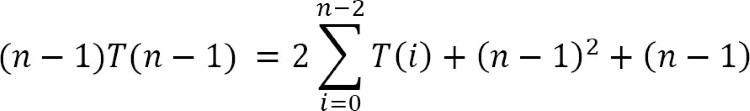
Lấy (1) trừ (2)

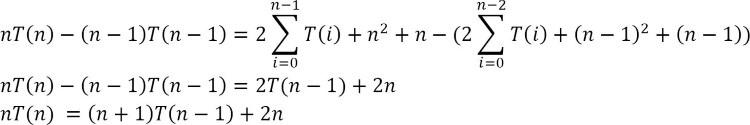
Chia hết cho n(n + 1).

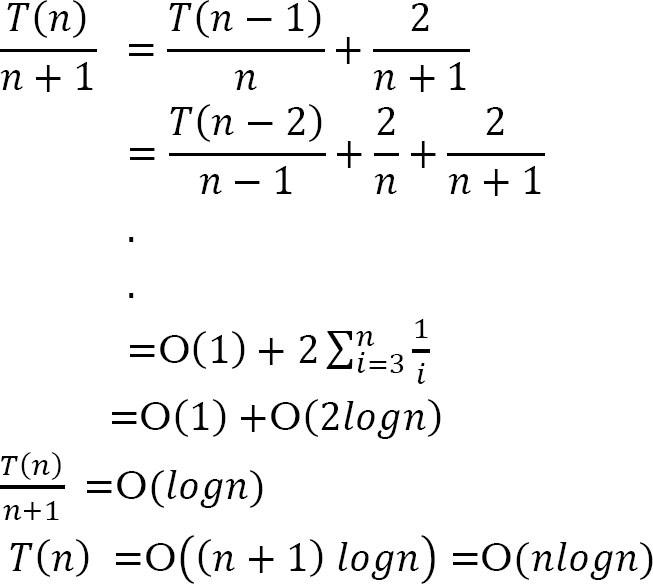
Time Complexity, $T(n) = O(nlogn)$.

Performance

Sắp xếp nhanh ngẫu nhiên

Trong hành vi trường hợp trung bình của Sắp xếp nhanh, chúng ta giả định rằng tất cả các hoán vị của các số đầu vào đều có khả năng xảy ra như nhau. Tuy nhiên, không phải lúc nào chúng ta cũng mong nó giữ được như thế. Chúng ta có thể thêm tính năng ngẫu nhiên vào một thuật toán để giảm xác suất xảy ra trường hợp xấu nhất trong Quick Sort.

Có hai cách để thêm ngẫu nhiên trong Sắp xếp nhanh: bằng cách đặt ngẫu nhiên dữ liệu đầu vào vào mảng hoặc bằng cách chọn ngẫu nhiên một phần tử trong dữ liệu đầu vào cho trục xoay. Sự thay đổi sẽ chỉ được thực hiện ở thuật toán Partition.

Trong sắp xếp nhanh thông thường, phần tử trục luôn là phần tử ngoài cùng bên trái(hoặc phải) trong danh sách cần sắp xếp. Thay vì luôn sử dụng A[low] làm trục, chúng ta sẽ sử dụng một phần tử được chọn ngẫu nhiên từ mảng con A[low..high] trong phiên bản ngẫu nhiên của Sắp xếp nhanh. Nó được thực hiện bằng cách trao đổi phần tử A[low] với một phần tử được chọn ngẫu nhiên từ A[low..high]. Điều này đảm bảo rằng phần tử trục có khả năng là bất kỳ phần tử $high – low + 1$ nào trong mảng con.

Vì phần tử trục được chọn ngẫu nhiên, chúng ta có thể mong đợi sự phân chia của mảng đầu vào được cân bằng hợp lý ở mức trung bình. Điều này có thể giúp ngăn chặn hành vi sắp xếp nhanh trong trường hợp xấu nhất xảy ra trong phân vùng không cân bằng.

Mặc dù phiên bản ngẫu nhiên cải thiện độ phức tạp của trường hợp xấu nhất, nhưng độ phức tạp trong trường hợp xấu nhất của nó vẫn là $O(n^2)$. Một cách để cải thiện Sắp xếp nhanh ngẫu nhiên là chọn trục để phân vùng cẩn thận hơn là chọn một phần tử ngẫu nhiên từ mảng. Một cách tiếp cận phổ biến là chọn trục làm trung vị của bộ 3 phần tử được chọn ngẫu nhiên từ mảng.

10.12 Tree Sort

Sắp xếp cây sử dụng cây tìm kiếm nhị phân. Nó liên quan đến việc quét từng phần tử của đầu vào và đặt nó vào vị trí thích hợp của nó trong cây tìm kiếm nhị phân. Điều này có hai giai đoạn:

• Giai đoạn đầu tiên là tạo cây tìm kiếm nhị phân bằng cách sử dụng các phần tử mảng đã cho.
• Giai đoạn thứ hai là duyệt cây tìm kiếm nhị phân đã cho theo thứ tự, do đó dẫn đến một mảng được sắp xếp.

Chi tiết các bạn có thể xem lại bài viết này

Performance

Số lần so sánh trung bình của phương pháp này là $O(nlogn)$. Nhưng trong trường hợp xấu nhất, số phép so sánh trở thành $O(n^2)$, một trường hợp phát sinh khi cây sắp xếp là cây lệch.

10.13 Comparison of Sorting Algorithms

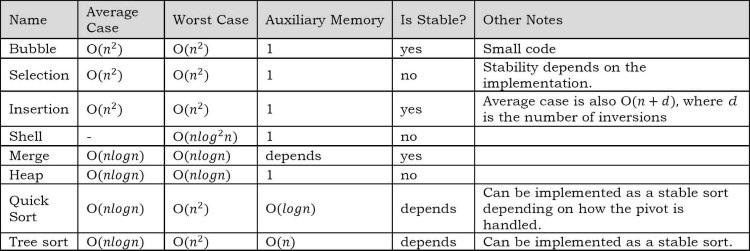
Lưu ý: n biểu thị số phần tử trong đầu vào.

10.14 Linear Sorting Algorithms

Trong các phần trước, chúng ta đã thấy nhiều ví dụ về thuật toán sắp xếp dựa trên so sánh. Trong số đó, sắp xếp dựa trên so sánh tốt nhất có độ phức tạp O(nlogn). Trong phần này, chúng ta sẽ thảo luận về các loại thuật toán khác: Linear Sorting Algorithms(Thuật toán sắp xếp tuyến tính). Để cải thiện độ phức tạp về thời gian của việc sắp xếp các thuật toán này, chúng ta đưa ra một số giả định về đầu vào. Một vài ví dụ về thuật toán sắp xếp tuyến tính là:

• Counting Sort
• Bucket Sort
• Radix Sort

10.15 Counting Sort

Counting Sort không phải là thuật toán sắp xếp dựa trên so sánh và đưa ra độ phức tạp $O(n)$ cho việc sắp xếp. Để đạt được độ phức tạp $O(n)$, sắp xếp đếm giả định rằng mỗi phần tử là một số nguyên trong phạm vi từ 1 đến K, đối với một số nguyên K. Khi $K = O(n)$, sắp xếp đếm chạy trong thời gian $O(n)$. Ý tưởng cơ bản của counting sort là xác định, đối với mỗi phần tử đầu vào X, số phần tử nhỏ hơn X. Thông tin này có thể được sử dụng để đặt nó trực tiếp vào đúng vị trí của nó. Ví dụ: nếu 10 phần tử nhỏ hơn X, thì X thuộc vị trí 11 trong đầu ra.

Trong đoạn mã dưới đây, $A[0 ..n – 1]$ là mảng đầu vào có độ dài n. Trong sắp xếp đếm, chúng ta cần thêm hai mảng: giả sử mảng $B[0 ..n – 1]$ chứa đầu ra đã sắp xếp và mảng $C[0 ..K – 1]$ cung cấp bộ nhớ tạm thời.

    public static void CountingSort(int[] A, int B[], int K){
        int C[] = new int[K];
        int i, j, n = A.length;
        for (i = 0; i < K; i++) {
            C[i] = 0;
        }

        //C[i] now contains the number of elements equal to i
        for(j = 0; j < n; j++){
            C[A[j]] = C[A[j]] + 1;
        }

        //C[i] now contains the number of elements <= i
        for (i = 1; i < K; i++) {
            C[i] = C[i] + C[i-1];
        }

        for(j = n-1; j >= 0; j--){
            B[C[A[j]]] = A[j];
            C[A[j]] = C[A[j]] - 1;
        }
    }

Total Complexity: $O(K) + O(n) + O(K) + O(n) = O(n)$ nếu $K =O(n)$.
Space Complexity: $O(n)$ nếu $K=O(n)$.

Lưu ý: Đếm hoạt động tốt nếu K = O(n). Nếu không, sự phức tạp sẽ lớn hơn.

10.16 Bucket Sort (or Bin Sort)

Giống như Counting sort, Bucket Sort cũng áp đặt các hạn chế đối với đầu vào để cải thiện hiệu suất. Nói cách khác, Bucket Sort hoạt động tốt nếu đầu vào được rút ra từ tập hợp cố định. Bucket sort là sự khái quát hóa của Counting Sort. Ví dụ: giả sử rằng tất cả các phần tử đầu vào từ ${0, 1, ..., K – 1}$, tức là tập hợp các số nguyên trong khoảng $[0, K – 1]$. Bucket Sort sử dụng K bộ đếm. Bộ đếm thứ i theo dõi số lần xuất hiện của phần tử thứ i. Bucket sort với hai nhóm thực sự là một phiên bản Quick sort với hai nhóm.

Đối với bucket sort, hash function(hàm băm) được sử dụng để phân vùng các phần tử cần phải rất tốt và phải tạo ra hàm băm có thứ tự: nếu $i < k$ thì $hash(i) < hash(k)$. Thứ hai, các phần tử được sắp xếp phải được phân bố đồng đều. Ngoài những điều đã nói ở trên, Bucket Sort thực sự rất tốt khi xét đến việc counting sort nói một cách hợp lý là giới hạn trên của nó. Và counting sort rất nhanh. Sự khác biệt cụ thể đối với Bucket Sort là nó sử dụng hàm băm để phân vùng các khóa của mảng đầu vào, sao cho nhiều khóa có thể băm vào cùng một nhóm. Do đó, mỗi nhóm phải thực sự là một danh sách có thể phát triển được; tương tự như radix sort.

Trong đoạn mã dưới đây, Insertionsort được sử dụng để sắp xếp từng nhóm. Điều này là để khắc sâu rằng thuật toán Bucket Sort không chỉ định kỹ thuật sắp xếp nào sẽ sử dụng trên các nhóm. Một lập trình viên có thể chọn sử dụng liên tục bucket sort trên mỗi nhóm cho đến khi toàn bộ được sắp xếp (theo cách của chương trình radix sort bên dưới). Cho dù phương pháp sắp xếp nào được sử dụng trên , bucket sort vẫn có xu hướng về O(n).

Code mình có tham khảo ở đây

// Bucket sort in Java

import java.util.ArrayList;
import java.util.Collections;

public class BucketSort {
  public void bucketSort(float[] arr, int n) {
    if (n <= 0)
      return;
    @SuppressWarnings("unchecked")
    ArrayList<Float>[] bucket = new ArrayList[n];

    // Create empty buckets
    for (int i = 0; i < n; i++)
      bucket[i] = new ArrayList<Float>();

    // Add elements into the buckets
    for (int i = 0; i < n; i++) {
      int bucketIndex = (int) arr[i] * n;
      bucket[bucketIndex].add(arr[i]);
    }

    // Sort the elements of each bucket
    for (int i = 0; i < n; i++) {
      Collections.sort((bucket[i]));
    }

    // Get the sorted array
    int index = 0;
    for (int i = 0; i < n; i++) {
      for (int j = 0, size = bucket[i].size(); j < size; j++) {
        arr[index++] = bucket[i].get(j);
      }
    }
  }

  // Driver code
  public static void main(String[] args) {
    BucketSort b = new BucketSort();
    float[] arr = { (float) 0.42, (float) 0.32, (float) 0.33, (float) 0.52, (float) 0.37, (float) 0.47,
        (float) 0.51 };
    b.bucketSort(arr, 7);

    for (float i : arr)
      System.out.print(i + "  ");
  }
}

Time Complexity: O(n). Space Complexity: O(n).

10.17 Radix Sort

Tương tự như Counting sort và Bucket sort, thuật toán sắp xếp này cũng giả định một số loại thông tin về các phần tử đầu vào. Giả sử rằng các giá trị đầu vào đều có số chữ số là d. Trong Radix sort, trước tiên hãy sắp xếp các phần tử dựa trên chữ số cuối cùng [chữ số ít quan trọng nhất]. Những kết quả này lại được sắp xếp theo chữ số thứ hai [chữ số bên cạnh chữ số ít quan trọng nhất]. Tiếp tục quá trình này cho tất cả các chữ số cho đến khi chúng ta đạt được các chữ số quan trọng nhất. Sử dụng một số stable sort để sắp xếp chúng theo chữ số cuối cùng. Sau đó, stable sort chúng theo chữ số có nghĩa nhỏ thứ hai, rồi đến chữ số thứ ba, v.v. Nếu chúng ta sử dụng Counting Sort làm sắp xếp ổn định, thì tổng thời gian là $O(nd) ≈ O(n)$.

Algorithm:

1. Lấy chữ số có nghĩa nhỏ nhất của mỗi phần tử.
2. Sắp xếp danh sách các phần tử dựa trên chữ số đó, nhưng giữ nguyên thứ tự của các phần tử có cùng chữ số (đây là định nghĩa của stable sort).
3. Lặp lại sắp xếp với mỗi chữ số quan trọng hơn.

Tốc độ của Radix sort phụ thuộc vào các operations cơ bản bên trong. Nếu các operations không đủ hiệu quả, Radix Sort có thể chậm hơn các thuật toán khác như Sắp xếp nhanh và Sắp xếp hợp nhất. Các thao tác này bao gồm các chức năng chèn và xóa của các danh sách phụ và quá trình cô lập chữ số mà chúng ta muốn. Nếu các số không có độ dài bằng nhau thì cần thực hiện phép thử để kiểm tra thêm các chữ số cần sắp xếp. Đây có thể là một trong những phần chậm nhất của Radix Sort và cũng là một trong những phần khó thực hiện hiệu quả nhất.

Vì Radix sort phụ thuộc vào các chữ số hoặc chữ cái nên nó kém linh hoạt hơn so với các cách sắp xếp khác. Đối với mọi loại dữ liệu khác nhau, Radix sort cần được viết lại và nếu thứ tự sắp xếp thay đổi, thì cách sắp xếp cần được viết lại. Nói tóm lại, Radix sort mất nhiều thời gian hơn để viết và rất khó để viết một Radix sort cho mục đích chung có thể xử lý tất cả các loại dữ liệu. Đối với nhiều chương trình cần sắp xếp nhanh, Radix sort là một lựa chọn tốt. Tuy nhiên, vẫn có những cách sắp xếp nhanh hơn, đó là một lý do tại sao Radix sort không được sử dụng nhiều như một số cách sắp xếp khác.

Trong sách tác giả không implement thuật toán này, các bạn có thể tham khảo thêm ở đây

Time Complexity: $O(nd) ≈ O(n)$, nếu d nhỏ.

10.19 External Sorting

External sorting là một thuật ngữ chung cho một lớp thuật toán sắp xếp có thể xử lý lượng dữ liệu khổng lồ. Các thuật toán này rất hữu ích khi các tệp quá lớn và không thể vừa với main memory. Cũng như các thuật toán internal sorting, có một số thuật toán external sorting. Một thuật toán như vậy là External Mergesort. Trong thực tế, các thuật toán external sorting này đang được bổ sung bởi các internal sorting.

Ví dụ đơn giản về External Mergesort

Một số bản ghi từ mỗi băng được đọc vào bộ nhớ chính, được sắp xếp bằng internal sorting, rồi xuất ra băng. Để rõ ràng, chúng ta hãy giả sử rằng 900 megabyte dữ liệu cần được sắp xếp chỉ bằng 100 megabyte RAM.

1. Đọc 100 MB dữ liệu vào bộ nhớ chính và sắp xếp theo một số phương pháp thông thường (giả sử Quick Sort).
2. Ghi dữ liệu đã sắp xếp vào đĩa.
3. Lặp lại bước 1 và 2 cho đến khi tất cả dữ liệu được sắp xếp theo khối 100MB. Bây giờ chúng ta cần hợp nhất chúng thành một tệp đầu ra được sắp xếp duy nhất.
4. Đọc 10 MB đầu tiên của mỗi đoạn được sắp xếp (gọi chúng là bộ đệm đầu vào) trong bộ nhớ chính (tổng cộng 90 MB) và phân bổ 10 MB còn lại cho bộ đệm đầu ra.
5. Thực hiện Mergesort 9 khối và lưu kết quả vào bộ đệm đầu ra. Nếu bộ đệm đầu ra đầy, hãy ghi nó vào tệp kết quả. Nếu bất kỳ bộ đệm đầu vào nào trong số 9 bộ đệm đầu vào bị trống, hãy lấp đầy nó bằng 10 MB tiếp theo trong số 100 MB đoạn được sắp xếp có liên quan của nó; hoặc nếu không còn dữ liệu nào trong đoạn đã sắp xếp, hãy đánh dấu nó là đã hết và không sử dụng nó để hợp nhất.

(Đây cũng là 1 câu hỏi mình từng gặp khi phòng vấn 😄)

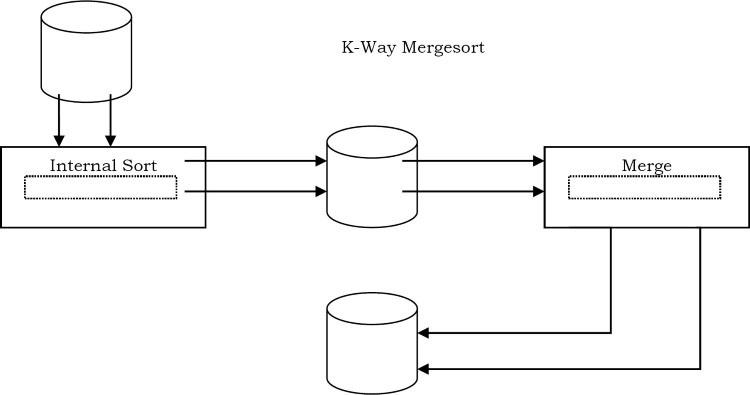
Thuật toán trên có thể được khái quát hóa bằng cách giả sử rằng lượng dữ liệu được sắp xếp vượt quá bộ nhớ khả dụng theo hệ số K. Sau đó, K khối dữ liệu cần được sắp xếp và hợp nhất K -way phải được hoàn thành.

Nếu X là dung lượng bộ nhớ chính khả dụng, thì sẽ có K bộ đệm đầu vào và 1 bộ đệm đầu ra có kích thước X/(K + 1) mỗi bộ. Tùy thuộc vào các yếu tố khác nhau (ổ cứng chạy nhanh như thế nào?) có thể đạt được hiệu suất tốt hơn nếu bộ đệm đầu ra được làm lớn hơn (ví dụ: lớn gấp đôi một bộ đệm đầu vào).