Chương 1: Introduction - 7.Các định lý chính về giải thuật Subtract and Conquer Recurrences

Divide and Conquer algorithm tiếng việt là Chia để trị thì có lẽ Subtract and Conquer algorithm là Trừ để trị 😅
Cái này mình không chắc có dịch ra đúng nghĩa không, nếu có sai sót các bạn comment nhé, mình sẽ sửa lại 😁

1.24 Master Theorem for Subtract and Conquer Recurrences

Vì trong sách tác giả viết về phần này khá ngắn gọn, mình có tham khảo thêm thông tin ở đây

Các định lý này được sử dụng để xác định độ phức tạp Big-O trên các hàm đệ quy ~ nghĩa là có thể chia nhỏ thành các bài toán con:

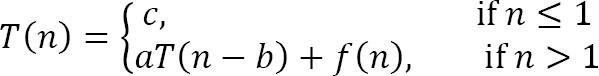
Với các hằng số c, a > 0, b > 0, k ≥ 0 và hàm f(n). Nếu f(n) có độ phức tạp $O ( n ^ { k } )$ thì

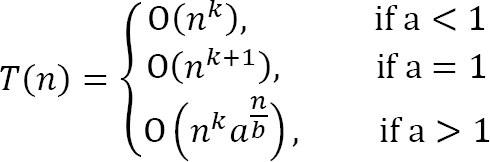
Chứng minh định lý:
Từ công thức ban đầu ta có:

1. T(n) = aT(n-b) + f(n)
2. T(n-b) = aT(n-2b) + f(n-b)
3. T(n-2b) = aT(n-3b) + f(n-2b)

=> $T \left ( n - b \right ) = a ^ { 2 } T \left ( n - 3 b \right ) + a f \left ( n - 2 b \right ) + f \left ( n - b \right )$ (Thay 3 vào 2)
=> $T \left ( n \right ) = a ^ { 3 } T \left ( n - 3 b \right ) + a ^ { 2 } f \left ( n - 2 b \right ) + a f \left ( n -b \right ) + f \left ( n \right )$ (Thay công thức trên vào 1)
=> T(n) = $\Sigma ^ { i = 0 \text { to n/b } }$ $a ^ { i } f ( n - i b )$ + constant, trong đó $f ( n - i b )$ có độ phức tạp $O ( n - i b )$
=> $T \left ( n \right ) = O \left ( n ^ { k } \Sigma ^ { i = 0 \text { to n } / b } a ^ { i } \right )$

=> Từ công thức này, ta có kết luận như ảnh 2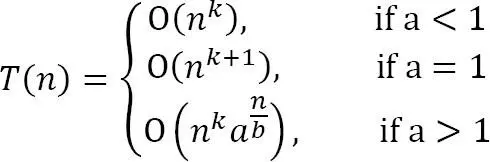
Các bạn có thể tham khảo chứng minh ở link sau

1.25 Variant of Subtraction and Conquer Master Theorem

Giải pháp cho phương trình $T ( n ) = T ( \alpha ~ n ) + T ( ( 1 - \alpha ) n ) + \beta n$, với 0 < α < 1 và β > 0 là các hằng số constant
là O(nlogn)

Bài toán ví dụ

Một bài toán tiêu biểu cho giải thuật này là tìm số fibonacci.
Quy luật của dãy số Fibonacci: số tiếp theo bằng tổng của 2 số trước, 2 số đầu tiên của dãy số là 0, 1. Ví dụ: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

class Fibonacci {
	static int findFibonacci(int n) {
		if (n <= 1)
			return n;
		return findFibonacci(n - 1) + findFibonacci(n - 2);
	}


	public static void main(String[] args) {
		int n = 9;
		System.out.println(findFibonacci(n));
	}
}

Phân tích Time complexity
Hàm đệ quy trên có thể được định nghĩa là T(n) = T(n-1) + T(n-2)
Trong trường hợp Worst Case, giả sử T(n-1) ≈ T(n-2)
=> T(n) = 2T(n-1) + c
Với f(n) = O(1) (hằng số c), k = 0, a = 2, b = 1
Áp dụng lý thuyết trên ta có:
$| T \left ( n \right ) = O \left ( n ^ { 0 } 2 ^ { n / 1 } \right )$ $= O \left ( 2 ^ { n } \right )$

Tạm kết lý thuyết về Subtract and Conquer, bài sau mình sẽ trình bày về Phương pháp phỏng đoán và xác nhận(Guessing and Confirming).
Bài viết có đôi chút khó về toán, cảm ơn mọi người đã đọc tới đây 😁