Chương 2: RECURSION AND BACKTRACKING - 2. Backtracking(Quay lui)

2.8 What is Backtracking?

Brute force approach là cách tiếp cận tìm ra tất cả các giải pháp có thể để tìm ra giải pháp thỏa đáng cho một vấn đề nhất định.
Backtracking là một cải tiến của brute force approach.
Nó tìm kiếm một cách có hệ thống giải pháp cho một vấn đề trong số tất cả các tùy chọn có sẵn.
Trong backtracking, chúng ta bắt đầu với một tùy chọn khả thi trong số nhiều tùy chọn có sẵn và cố gắng giải quyết vấn đề nếu chúng ta có thể giải quyết vấn đề với nước đi đã chọn thì chúng ta sẽ in ra giải pháp khác nếu không chúng ta sẽ quay lại và chọn một số tùy chọn khác và cố gắng giải quyết nó.
Nếu không có tùy chọn nào, chúng tôi sẽ tuyên bố rằng không có giải pháp cho vấn đề.
Backtracking là một dạng đệ quy.
Tình huống thông thường là ta phải đối mặt với một số lựa chọn và ta phải chọn một trong những lựa chọn này.
Sau khi bạn lựa chọn, bạn sẽ nhận được một tập hợp các tùy chọn mới, phụ thuộc vào lựa chọn bạn đã thực hiện.
Quá trình này được lặp đi lặp lại cho đến khi bạn đạt được trạng thái cuối cùng.
Nếu ta thực hiện một chuỗi lựa chọn tốt, trạng thái cuối cùng là trạng thái mục tiêu.
Backtracking có thể được coi là một phương pháp duyệt đồ thị / cây có chọn lọc.
Tree là một cách thể hiện một số vị trí bắt đầu ban đầu (nút gốc) và trạng thái mục tiêu cuối cùng (một trong các lá).
Backtracking cho phép chúng ta đối phó với các tình huống trong đó Brute force approach sẽ bùng nổ thành một số lượng lựa chọn quá lớn không thể xem xét.
Tại mỗi nút, chúng tôi loại bỏ các lựa chọn rõ ràng là không thể và chỉ tiến hành kiểm tra đệ quy những lựa chọn có tiềm năng.
Điều thú vị về backtracking là chúng ta chỉ sao lưu khi cần thiết để đạt được điểm quyết định trước đó với một giải pháp thay thế chưa được khám phá.
Nói chung, đó sẽ là thời điểm quyết định gần đây nhất.
Cuối cùng, ngày càng nhiều điểm quyết định này sẽ được khám phá đầy đủ và chúng ta sẽ phải quay lui ngày càng xa hơn.
Nếu chúng ta quay ngược lại tất cả các con đường về trạng thái ban đầu của mình và đã khám phá tất cả các lựa chọn thay thế từ đó, chúng ta có thể kết luận rằng vấn đề cụ thể là không thể giải quyết được.
Trong trường hợp như vậy, chúng ta sẽ thực hiện tất cả các công việc của đệ quy đầy đủ và biết rằng không có giải pháp khả thi nào có thể xảy ra.

• Đôi khi thuật toán tốt nhất cho một vấn đề là thử tất cả các khả năng
• Điều này luôn luôn chậm, nhưng có những công cụ tiêu chuẩn có thể được sử dụng để trợ giúp.
• Tools: các thuật toán để tạo ra các basic objects(đối tượng cơ bản), như là các chuỗi nhị phân ($2^n$ khả năng cho n-bit string), hoán vị($n!$), kết hợp ($n! / r! (n - r)!$), chuỗi tổng quát (k – chuỗi có độ dài n có $k^n$ khả năng), ...
• Backtracking tăng tốc độ tìm kiếm toàn diện bằng cách cắt tỉa.

2.9 Các ví dụ về thuật toán Backtracking?

• Binary Strings
• Generating k – ary Strings
• The Knapsack Problem
• N-Queens Problem
• Generalized Strings
• Hamiltonian Cycles(Chi tiết sẽ trình bày ở chương Graphs)
• Graph Coloring Problem

Problem-3

Tạo tất cả các chuỗi n bit. Giả sử A [0..n - 1] là một mảng có kích thước n.

Solution:

	public static void main(String[] args) {
		int n = 4;
		int A[] = new int[n];
		Binary(n, A);
	}
	

	public static void Binary(int n, int A[]) {
		if(n < 1) {
			System.out.println(Arrays.toString(A));
		} else {
			A[n-1] = 0;
			Binary(n-1, A);
			A[n-1] = 1;
			Binary(n-1, A);
		}
	}

Và kết quả khi mình thử với n = 4, các bạn có thể thử với các n khác nhau và xem kết quả nhé;

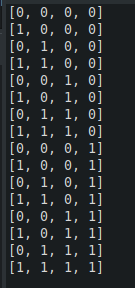
Problem-4

Tạo tất cả các chuỗi có độ dài n với các giá trị từng phần tử là từ $0 ... k - 1$.

Solution: Giả sử chuỗi ta cần nằm trong mảng $A[0 .. n-1]$

	public static void main(String[] args) {
		int n = 4;
		int A[] = new int[n];
		k_string(n, 3, A);
	}

	public static void k_string(int n, int k, int A[]) {
		if (n < 1) {
			System.out.println(Arrays.toString(A));
		} else {
			for (int i = 0; i < k; i++) {
				A[n-1] = i;
				k_string(n-1, k, A);
			}
		}
	}

Đây là 1 phần kết quả khi mình thử với n = 4 và k = 3.

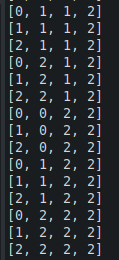
Coi T(n) là running time của hàm k_string(n, k), ta có

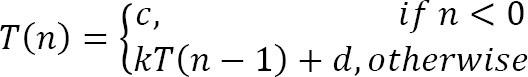
Sử dụng Subtraction and Conquer Master theorem ta được:
$T(n) = O(n^k)$

Problem-5

Tìm độ phức tạp: $T(n) = 2T(n – 1) + 2^n$

Solution:
Ở mỗi level của cây tái hiện, số lượng vấn đề gấp đôi so với cấp trước đó, trong khi lượng công việc được thực hiện trong mỗi vấn đề bằng một nửa so với cấp trước đó.
Về mặt hình thức, level thứ i có $2^i$ bài toán, mỗi bài toán yêu cầu $2 ^ { n - i }$ công việc.
Do đó, ở level i yêu cầu chính xác $2^n$ công việc. Độ sâu của cây là n => Tổng độ phức tạp là $O(n2^n)$