Chương 6: TREES - 5.Lý thuyết về duyệt cây nhị phân theo luồng(Threaded binary tree traversals)
Bài đăng này đã không được cập nhật trong 2 năm
6.6 Threaded (Stack or Queue less) Binary Tree Traversals
Trong các phần trước, chúng ta đã thấy rằng, việc duyệt preorder, inorder, và postorder binary tree đã sử dụng stack và duyệt theo level order traversal đã sử dụng queue làm cấu trúc dữ liệu phụ trợ. Trong phần này, chúng ta sẽ thảo luận về các thuật toán duyệt mới không cần cả ngăn xếp và hàng đợi. Các thuật toán duyệt như vậy được gọi là duyệt cây nhị phân theo luồng(threaded binary tree traversals) hoặc duyệt ít ngăn xếp/hàng đợi hơn(stack/queue less traversals).
Các vấn đề với duyệt cây nhị phân thông thường
- Không gian lưu trữ cần thiết cho ngăn xếp và hàng đợi lớn.
- Phần lớn các con trỏ trong bất kỳ cây nhị phân nào là NULL. Ví dụ, một cây nhị phân với n node có n + 1 con trỏ NULL và chúng đã bị lãng phí.
- Rất khó để tìm node kế tiếp (preorder, inorder and postorder) cho một node nhất định.

Khái niệm về Successor/Predecessor trong cây nhị phân
Phần về Successor(Kế nhiệm) và Predecessor(Tiền nhiệm) trong sách tác giả không nhắc đến nên mình có tham khảo ở đây và ở đây, chúng ta cần hiểu nó là gì trước khi đi tiếp.
Ví dụ với Inorder Successor trong cây nhị phân.

Trong Cây nhị phân, Inorder successor của một node là node tiếp theo trong quá trình duyệt Inorder traversal của Cây nhị phân. Inorder Successor là NULL cho node cuối cùng trong Inorder traversal. Khái niệm tương tự cho Inorder Predecessor
Động lực cho Threaded Binary Trees
Để giải quyết những vấn đề này, một ý tưởng là lưu trữ một số thông tin hữu ích trong các NULL pointers(Các node lá trỏ tới node trái, phải đều là null, chúng ta sẽ tận dụng chúng). Nếu chúng ta quan sát kỹ các lần duyệt trước, thì cần phải có ngăn xếp/hàng đợi vì chúng ta phải ghi lại vị trí hiện tại để chuyển sang cây con bên phải sau khi xử lý cây con bên trái. Nếu chúng tôi lưu trữ thông tin hữu ích trong NULL pointers, thì chúng tôi không phải lưu trữ thông tin đó trong ngăn xếp/hàng đợi.
Cây nhị phân lưu trữ thông tin như vậy trong NULL pointers được gọi là cây nhị phân luồng. Từ cuộc thảo luận ở trên, giả sử rằng chúng ta muốn lưu trữ một số thông tin hữu ích trong các con trỏ NULL. Câu hỏi tiếp theo là lưu trữ cái gì?
Quy ước chung là đặt thông tin tiền nhiệm/kế nhiệm(predecessor/successor). Điều đó có nghĩa là, nếu chúng ta đang xử lý preorder traversals, thì đối với một node nhất định, NULL left pointer sẽ chứa thông tin tiền nhiệm(preorder predecessor information) và NULL right pointer sẽ chứa thông tin kế nhiệm(preorder successor information).
Những con trỏ đặc biệt này được gọi là threads.
Phân loại Threaded Binary Trees
Việc phân loại dựa trên việc chúng tôi đang lưu trữ thông tin hữu ích trong cả hai con trỏ NULL hay chỉ trong một trong số chúng.
- Nếu chúng ta chỉ lưu trữ thông tin tiền nhiệm trong các NULL left pointers thì chúng ta gọi những cây nhị phân đó là left threaded binary trees.
- Nếu chúng ta chỉ lưu trữ thông tin kế nhiệm trong NULL right pointers thì chúng ta gọi những cây nhị phân đó là right threaded binary trees.
- Nếu chúng ta lưu trữ thông tin tiền nhiệm trong NULL left pointers và lưu trữ thông tin kế nhiệm trong NULL right pointers, thì chúng ta gọi cây nhị phân đó là fully threaded binary trees hoặc simply threaded binary trees.
Lưu ý: Đối với các cuộc thảo luận còn lại, chúng ta chỉ xem xét fully threaded binary trees.
Các loại Threaded Binary Trees
Dựa trên cuộc thảo luận ở trên, chúng ta thấy được ba biểu diễn cho cây nhị phân theo luồng.
- Preorder Threaded Binary Trees: NULL left pointer chứa thông tin tiền nhiệm của PreOrder và NULL right pointer chứa thông tin kế nhiệm của PreOrder.
- Inorder Threaded Binary Trees: NULL left pointer chứa thông tin tiền nhiệm của Inorder và NULL right pointer chứa thông tin kế nhiệm của Inorder.
- Postorder Threaded Binary Trees: NULL left pointer chứa thông tin tiền nhiệm của Postorder và NULL right pointer chứa thông tin kế nhiệm của Postorder.
Lưu ý: Vì các biểu diễn tương tự nhau nên đối với cuộc thảo luận còn lại, chúng ta sẽ sử dụng cây nhị phân InOrderthreaded.
Cấu trúc của Threaded Binary Tree
Bất kỳ chương trình nào kiểm tra cây phải có khả năng phân biệt giữa con trỏ left/right thông thường và thread. Để làm điều này, chúng tôi sử dụng hai trường bổ sung trong mỗi node, cung cấp cho chúng ta, đối với cây phân luồng, các node có dạng sau:


Sự khác biệt giữa cấu trúc cây nhị phân và cây nhị phân theo luồng
| Cây nhị phân thông thường | Cây nhị phân theo luồng | |
|---|---|---|
| Nếu LTag == 0 | NULL | Con trỏ trái sẽ trỏ tới in-order tiền nhiệm |
| Nếu LTag == 1 | Con trỏ trái sẽ trỏ tới node con bên trái | Con trỏ trái sẽ trỏ tới node con bên trái |
| Nếu RTag == 0 | NULL | Con trỏ phải sẽ trỏ tới in-order kế nhiệm |
| Nếu RTag == 1 | Con trỏ phải sẽ trỏ tới node con bên phải | Con trỏ phải sẽ trỏ tới node con bên phải |
Ghi chú: Chúng ta cũng có thể xác định sự khác biệt về preorder/postorder tương tự.
Ví dụ, chúng ta hãy thử biểu diễn một cây ở dạng inorder threaded. Cây dưới đây cho thấy cây nhị phân theo luồng inorder sẽ trông như thế nào. Các mũi tên chấm chỉ các thread. Nếu chúng ta quan sát, con trỏ bên trái của node bên trái nhất (2) và con trỏ bên phải của node bên phải nhất (31) đang treo(không trỏ tới đâu cả).
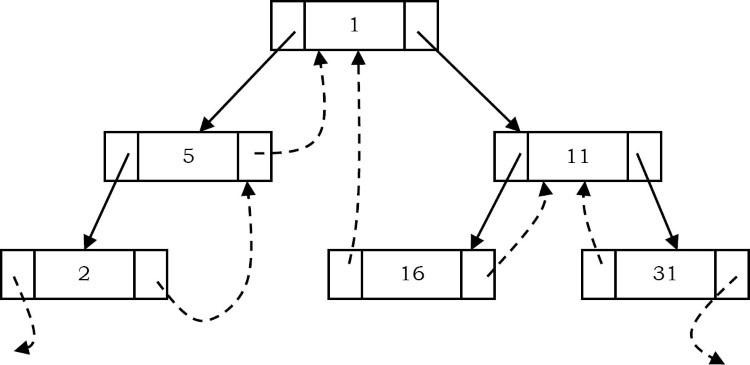
Con trỏ ngoài cùng bên trái và ngoài cùng bên phải nên trỏ tới cái gì?
Trong biểu diễn của cây nhị phân theo luồng, thật thuận tiện khi sử dụng node giả Dummy đặc biệt luôn xuất hiện ngay cả đối với cây trống. Lưu ý rằng thẻ bên phải của node Giả là 1 và con bên phải của nó trỏ đến chính nó.

Với quy ước này, cây trên có thể được biểu diễn dưới dạng:

Tìm Inorder Successor trong cây nhị phân theo luồng Inorder
Để tìm inorder successor của một node nhất định mà không sử dụng ngăn xếp, giả sử rằng node mà chúng ta muốn tìm node inorder successor là P. Chiến lược: Nếu P không có cây con bên phải, thì trả về con bên phải của P. Nếu P có cây con bên phải, thì trả về bên trái của node gần nhất có cây con bên trái chứa P.
public ThreadedBinaryTreeNode findInorderSuccessor(ThreadedBinaryTreeNode P){
ThreadedBinaryTreeNode Position;
if(P.getRTag() == 0){
return P.getRight();
} else{
Position = P.getRight();
while(Position.getLtag() == 1){
Position = Position.getLeft();
}
return Position;
}
}
Time Complexity: O(n). Space Complexity: O(1).
Inorder Traversal in Inorder Threaded Binary Tree
Chúng ta có thể bắt đầu với node giả Dummy và gọi InorderSuccessor() để truy cập từng node cho đến khi chúng ta đến node giả.
public void InorderTraversal(ThreadedBinaryTreeNode root){
ThreadedBinaryTreeNode P = findInorderSuccessor(root);
while(P != root){
P = findInorderSuccessor(P);
System.out.println(P.getData());
}
}
Time Complexity: O(n). Space Complexity: O(1).
Tìm kiếm PreOrder Successor trong InOrder Threaded Binary Tree
Chiến lược: Nếu P có cây con bên trái, thì trả về node con bên trái của P. Nếu P không có cây con bên trái, thì trả về node con bên phải của node gần nhất có cây con bên phải chứa P.
public ThreadedBinaryTreeNode findPreorderSuccessor(ThreadedBinaryTreeNode P){
ThreadedBinaryTreeNode Position;
if(P.getLtag()){
return P.getLeft();
} else{
Position = P;
while(Position.getRTag() == 0){
Position.getRight();
}
return Position.getRight();
}
}
PreOrder Traversal of InOrder Threaded Binary Tree
Như trong quá trình duyệt inorder traversal, hãy bắt đầu với node giả dummy và gọi findPreorderSuccessor() để truy cập từng node cho đến khi chúng tôi nhận lại node giả.
public void PreoderTraversal(ThreadedBinaryTreeNode root){
ThreadedBinaryTreeNode P = findPreorderSuccessor(root);
while(P != root){
P = findPreorderSuccessor(P);
System.out.println(P.getData());
}
}
Time Complexity: O(n). Space Complexity: O(1).
Lưu ý: Từ cuộc thảo luận ở trên, rõ ràng là việc tìm kiếm người kế vị theo thứ tự và đặt hàng trướcinorder and preorder successor là dễ dàng với các threaded binary trees. Nhưng việc tìm postorder successor là rất khó khăn nếu chúng ta không sử dụng ngăn xếp.
Chèn thêm node vào InOrder Threaded Binary Trees
Để đơn giản, chúng ta hãy giả sử rằng có hai node P và Q và chúng ta muốn gắn Q vào bên phải của P. Đối với điều này, chúng ta sẽ có hai trường hợp.
- node P không có con phải: Trong trường hợp này, chúng ta chỉ cần gắn Q vào P và thay đổi con trỏ trái và phải của nó.
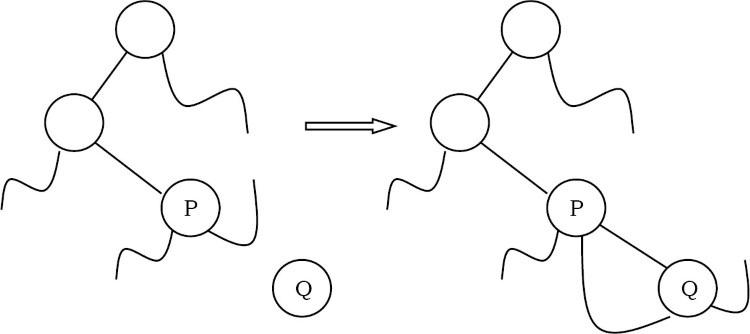
- node P có con bên phải (giả sử R): Trong trường hợp này, chúng ta cần duyệt qua cây con bên trái của R và tìm node bên trái nhất, sau đó cập nhật con trỏ bên trái và bên phải của node đó (như hình bên dưới).

public void insertRightInInorderTBT(ThreadedBinaryTreeNode P, ThreadedBinaryTreeNode Q){
ThreadedBinaryTreeNode Temp;
Q.setRight(P.getRight());
Q.setRTag(P.getRTag());
Q.setLeft(P);
Q.setLtag(0);
P.setRight(Q);
P.setRTag(1);
if(Q.getRTag() == 1){ //Case-2
Temp = Q.getRight();
while(Temp.getLtag() == 1){
Temp = Temp.getLeft();
}
Temp.setLeft(Q);
}
}
Time Complexity: O(n). Space Complexity: O(1).
Đây là một bài viết khá khó và trừu tượng với ý tưởng tận dụng các node lá mà đang trỏ tới null một cách vô ích. Các bạn có thể tham khảo thêm ở các link sau: ở đây và ở đây
All rights reserved