Chương 4: STACKS - Problems & Solutions(15-29)

Problem-15

Làm thế nào để triển khai 3 stack trong một array?

Solution: Đối với vấn đề này, có thể có những cách khác nhau để giải quyết nó. Dưới đây là một cách và nó hoạt động miễn là có một không gian trống trong mảng.

Để thực hiện 3 stack, chúng ta giữ các thông tin sau.

• Chỉ số của ngăn xếp đầu tiên (Top 1): chỉ số này cho biết kích thước của ngăn xếp đầu tiên.
• Chỉ số của ngăn xếp thứ hai (Top2): chỉ số này cho biết kích thước của ngăn xếp thứ hai.
• Chỉ mục bắt đầu của ngăn xếp thứ ba (địa chỉ cơ sở của ngăn xếp thứ ba).
• Chỉ số của ngăn xếp thứ hai (Top3)

Bây giờ, chúng ta hãy xác định các hoạt động push và pop cho việc triển khai này.

Pushing:

• Để push lên ngăn xếp đầu tiên, chúng ta cần xem liệu việc thêm một phần tử mới có khiến nó va vào ngăn xếp thứ ba hay không. Nếu có, hãy cố gắng chuyển ngăn xếp thứ ba lên trên. Chèn phần tử mới tại (start1 + Top1).
• Để push đến ngăn xếp thứ hai, chúng ta cần xem liệu việc thêm một phần tử mới có khiến nó va vào ngăn xếp thứ ba hay không. Nếu có, hãy cố gắng chuyển ngăn xếp thứ ba xuống dưới. Chèn phần tử mới tại (start2 - Top2).
• Khi push đến ngăn xếp thứ ba, hãy xem nó có đụng vào ngăn xếp thứ hai hay không. Nếu có, hãy thử chuyển ngăn xếp thứ ba xuống dưới và thử đẩy lại. Chèn phần tử mới tại (start3 + Top3).

Time Complexity: O(n). Vì chúng ta cần căn chỉnh stack3.
Space Complexity: O(1).

Popping: Đối với pop, chúng tôi không cần phải thay đổi, chỉ cần giảm kích thước của ngăn xếp thích hợp.
Time Complexity: O(1). Space Complexity: O(1).

Problem-16

Đối với Problem-15, có cách nào khác để triển khai middle stack không?

Solution: Yes. Khi ngăn xếp bên trái (phát triển sang bên phải) hoặc ngăn xếp bên phải (phát triển sang trái) chạm vào ngăn xếp giữa, chúng ta cần phải dịch chuyển toàn bộ ngăn xếp ở giữa để nhường chỗ. Điều tương tự cũng xảy ra nếu push ở ngăn xếp ở giữa khiến nó va vào ngăn xếp bên phải.

Để giải quyết vấn đề nêu trên (số lần dịch chuyển), những gì chúng ta có thể làm là: Các lần đẩy xen kẽ có thể được thêm vào các bên xen kẽ của danh sách giữa (Ví dụ: các phần tử chẵn được đẩy sang trái, các phần tử lẻ được đẩy sang phải). Điều này sẽ giữ cho ngăn xếp ở giữa được cân bằng ở trung tâm của mảng nhưng nó vẫn cần phải được dịch chuyển khi nó va vào ngăn xếp bên trái hoặc bên phải, cho dù bằng cách tự phát triển hoặc bằng cách tăng lên của một ngăn xếp lân cận.

Chúng tôi có thể tối ưu hóa các vị trí ban đầu của ba ngăn xếp nếu chúng phát triển / thu nhỏ ở các tốc độ khác nhau và nếu chúng có kích thước trung bình khác nhau. Ví dụ: giả sử một ngăn xếp không thay đổi nhiều. Nếu chúng ta đặt nó ở bên trái, thì ngăn xếp ở giữa cuối cùng sẽ bị đẩy vào nó và để lại một khoảng trống giữa ngăn xếp giữa và phải, chúng sẽ phát triển về phía nhau. Nếu chúng va chạm, thì có khả năng chúng ta đã hết dung lượng trong mảng. Không có thay đổi về độ phức tạp về thời gian nhưng số lần dịch chuyển trung bình sẽ giảm xuống.

Problem-17

Điều gì sẽ xảy ra nếu chúng ta muốn triển khai m ngăn xếp trong một mảng?

Solution: Chúng ta hãy giả sử rằng các chỉ mục mảng là từ 1 đến n. Tương tự như thảo luận trong Problem-15, để thực hiện m ngăn xếp trong một mảng, chúng ta chia mảng thành m phần (như hình dưới đây). Kích thước của mỗi phần là $\frac { n } { m }$.

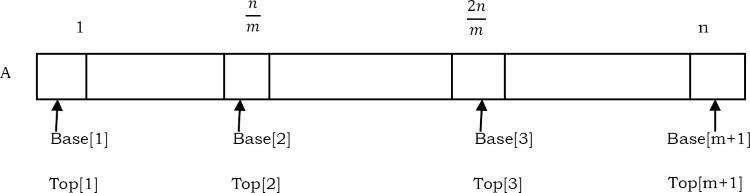
Từ biểu diễn trên, chúng ta có thể thấy rằng, ngăn xếp đầu tiên đang bắt đầu ở index 1(chỉ mục bắt đầu được lưu trữ trong Base[1]), ngăn xếp thứ hai đang bắt đầu tại index $\frac { n } { m }$(chỉ mục bắt đầu được lưu trữ trong Base[2]),. ngăn xếp thứ ba đang bắt đầu tại index $\frac { 2n } { m }$(chỉ mục bắt đầu được lưu trữ trong Base[3]). Tương tự như Base array, chúng ta hãy giả sử rằng Top array lưu trữ các chỉ mục hàng đầu cho mỗi ngăn xếp.

• $Top [i]$, với $1 ≤ i ≤ m$ sẽ trỏ đến phần tử trên cùng của ngăn xếp thứ i.
• Nếu $Base [i] == Top [i]$, thì chúng ta có thể nói rằng ngăn xếp thứ i trống.
• Nếu $Top [i] == Base [i + 1]$, thì chúng ta có thể nói rằng ngăn xếp thứ i đã đầy. Ban đầu $Base [i] = Top [i] = \frac { n } { m }(i - 1)$, với $1 ≤ i ≤ m$.
• Ngăn xếp thứ i tăng từ $Base[i]+1$ đến $Base[i+1]$.

Pushing vào stack thứ i

1. Để push vào ngăn xếp thứ i, chúng ta kiểm tra xem liệu đỉnh của ngăn xếp thứ i có trỏ đến Cơ sở [i + 1] hay không (trường hợp này xác định rằng ngăn xếp thứ i đã đầy). Điều đó có nghĩa là, chúng ta cần xem liệu việc thêm một phần tử mới có khiến nó va vào ngăn xếp thứ i + 1 hay không. Nếu có, hãy cố gắng chuyển các stack từ stack thứ i + 1 tới stack thứ m về phía bên phải. Chèn phần tử mới tại $(Base [i] + Top [i])$.
2. Nếu không thể dịch chuyển sang phải thì hãy thử chuyển các stack từ stack thứ nhất tới thứ $i - 1$ về phía bên trái.
3. Nếu cả hai đều không thể thực hiện được thì chúng ta có thể nói rằng tất cả các ngăn xếp đã đầy.

public void Push(int StackID, int data){
    if(Top[1] == Base[i+1])
            Print ith Stack is full and does the nesscessary action(shifting)
     
     Top[i] = Top[i]+1;
     A[Top[i]] = data;
}

Time Complexity: O(n). Vì chúng ta cần dịch chuyển các Stack.
Space Complexity: O(1).

Popping từ stack thứ i: Đối với popping, chúng tôi không cần phải thay đổi, chỉ cần giảm kích thước của ngăn xếp thích hợp. Trường hợp duy nhất chúng ta cần kiểm tra là trường hợp trống ngăn xếp.

public int Pop(int StackID){
    if(Top[i] == Base[i])
            Print ith Stack is empty
            
    return A[Top[i]--];
}

Time Complexity: O(1). Space Complexity: O(1).

Problem-18

Cho 1 Stack trống. Push các số 1,2,3,4,5,6 vào stack theo thứ tự xuất hiện từ trái sang phải. Giả sử ký hiệu S tương ứng với một lần push, X tương ứng một lần pop. Chúng có thể được hoán vị theo thứ tự 325641 (output) và thứ tự 154623 không? (Nếu một hoán vị có thể xảy ra, hãy cung cấp chuỗi hoạt động theo thứ tự. (Ví dụ: SSSSSSXXXXXX outputs 654321)

Solution: SSSXXSSXSXXX sẽ cho ra 325641. Không thể xuất 154623 vì t thấy 2 số cuối cùng là 23, 2 được push trước 3 nên chỉ có thể xuất hiện sau 3.

Problem-19

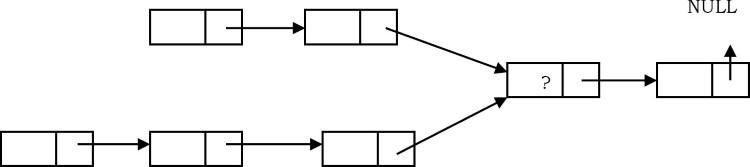
Bài toán tìm điểm giao của 2 linked list, mình đã trình bày trong chương 3 - Problem21

Problem-20

Trước đó trong chương này, chúng ta đã thảo luận rằng để triển khai mảng động của ngăn xếp, phương pháp 'repeated doubling' được sử dụng. Đối với cùng một bài toán, độ phức tạp là bao nhiêu nếu chúng ta tạo một mảng mới có kích thước là $n + K$ thay vì tăng gấp đôi?

Solution: Giả sử rằng kích thước ngăn xếp ban đầu là 0. Để đơn giản, chúng ta hãy giả sử rằng K = 10.
Để chèn phần tử, chúng ta tạo một mảng mới có kích thước là 0 + 10 = 10.
Tương tự, sau 10 phần tử, chúng ta lại tạo một mảng mới có kích thước là 10 + 10 = 20 và quá trình này tiếp tục ở các giá trị: 30, 40 ...
Điều đó có nghĩa là, với một giá trị n cho trước, chúng ta đang tạo các mảng mới tại: $\frac { n } { 4 0 } , \frac { n } { 2 0 } , \frac { n } { 3 0 } , \frac { n } { 3 0 } , \frac { n } { 4 0 } \ldots$
Tổng số lần phải thực hiện sao chép là:
$= \frac { n } { 4 0 } \pm \frac { n } { 2 0 } + \frac { n } { 3 0 } + \cdots 1 = \frac { n } { 1 0 } ( \frac { 1 } { 1 } + \frac { 1 } { 2 } + \frac { 1 } { 3 } \dagger \cdots \frac { 1 } { n } ) = \frac { n } { 1 0 } l o g n \approx O ( n L o g n)$

Nếu chúng ta đang thực hiện n lần push, chi phí cho mỗi hoạt động là $O (logn)$.

Problem-21

Cho một chuỗi chứa n kí hiệu S và n kí hiệu X, trong đó S chỉ ra một thao tác push và X chỉ ra thao tác pop và X với ngăn xếp ban đầu trống, hãy xây dựng một quy tắc để kiểm tra xem một chuỗi S hoạt động nhất định có được chấp nhận hay không?

Solution: Với một chuỗi có độ dài 2n, chúng ta muốn kiểm tra xem chuỗi hoạt động đã cho có được phép hay không đối với hoạt động của nó trên một ngăn xếp. Hoạt động bị hạn chế duy nhất là cửa sổ bật có yêu cầu trước là ngăn xếp không được để trống. Vì vậy, trong khi duyệt qua chuỗi từ trái sang phải, trước bất kỳ cửa sổ bật nào, ngăn xếp không được để trống, có nghĩa là số lượng S luôn lớn hơn hoặc bằng số lượng X. Do đó, điều kiện là ở bất kỳ giai đoạn xử lý nào của chuỗi, số lượng hoạt động push (S) phải lớn hơn số lượng hoạt động pop (X).

Problem-22

Tìm các nhịp: Cho một mảng A có $S [i]$ của $A [i]$ là số lượng phần tử lớn nhất của các phần tử liên tiếp $A [j]$ ngay trước $A [i]$ và sao cho $A [j] ≤ A [j + 1]$?
Một cách hỏi khác: Cho một mảng A gồm các số nguyên, hãy tìm giá trị lớn nhất của $j - i$ với ràng buộc $A [i] <A [j]$.

Solution: Đây là một vấn đề rất phổ biến trong các thị trường chứng khoán để tìm các đỉnh. Các khoảng thời gian được sử dụng trong phân tích tài chính (Ví dụ: cổ phiếu ở mức cao nhất trong 52 tuần). Khoảng thời gian của giá cổ phiếu vào một ngày nhất định, $i$, là số ngày liên tục tối đa (tính đến ngày hiện tại) giá cổ phiếu nhỏ hơn hoặc bằng giá của nó vào ngày thứ $i$.
Để làm ví dụ, chúng ta hãy xem xét bảng và biểu đồ nhịp tương ứng. Trong hình vẽ các mũi tên chỉ độ dài của các nhịp.

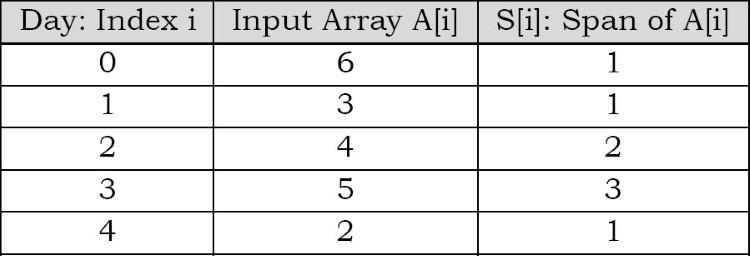
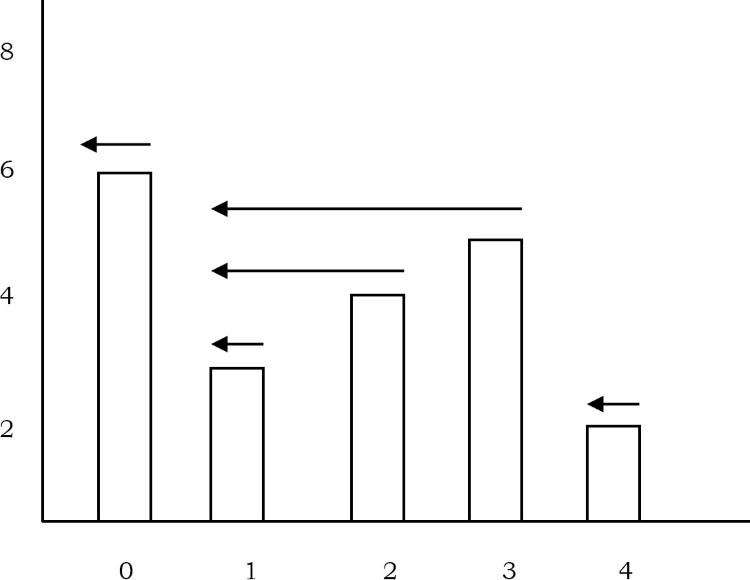
Bây giờ, chúng ta hãy tập trung vào thuật toán tìm các nhịp. Một cách đơn giản là mỗi ngày, hãy kiểm tra xem có bao nhiêu ngày liền kề có giá cổ phiếu nhỏ hơn giá hiện tại.

	public int[] FindingSpans(int[] inputArray) {
		int[] spans = new int[inputArray.length];
		for(int i = 0; i < inputArray.length; i++) {
			int span = 1;
			int j = i-1;
			while(j >= 0 && inputArray[j] <= inputArray[j+1]) {
				span++;
				j--;
			}
			spans[i] = span;
		}
		return spans;
	}

Time Complexity: O(n2). Space Complexity: O(1).

Problem-23

Chúng ta có thể cải thiện mức độ phức tạp của Problem-22 không?

Solution: Yes, từ ví dụ trên, chúng ta có thể thấy rằng khoảng $S [i]$ vào ngày thứ $i$ có thể dễ dàng tính được nếu chúng ta biết ngày gần nhất trước ngày thứ i, sao cho giá trị của ngày đó lớn hơn giá trị của ngày thứ $i$.
Hãy để chúng tôi gọi một ngày như vậy là $P$.
Nếu một ngày như vậy tồn tại thì khoảng thời gian bây giờ được xác định là $S [i] = i - P$.

	public int[] FindingSpans(int[] inputArray) {
		int[] spans = new int[inputArray.length];
		Stack stack = new Stack();
		int p = 0;
		for(int i = 0; i < inputArray.length; i++) {
			while(stack.isEmpty() == false && inputArray[i] > inputArray[(int) stack.peek()]) {
				stack.pop();
			}
			if(stack.isEmpty()) {
				p = -1;
			} else{
				p = (int) stack.peek();
			}
			spans[i] = i - p;
			stack.push(i);
		}
		return spans;
	}

**Time Complexity: **Mỗi index của mảng được đẩy vào ngăn xếp chính xác một lần và cũng chỉ được pop từ ngăn xếp nhiều nhất một lần. Các câu lệnh trong vòng lặp while được thực hiện nhiều nhất n lần. Mặc dù thuật toán có các vòng lặp lồng nhau, độ phức tạp là $O (n)$ vì vòng lặp bên trong chỉ thực hiện $n$ lần trong suốt quá trình của thuật toán (bạn hãy thử chạy một ví dụ và trace xem bao nhiêu lần vòng lặp bên trong thành công).

Space Complexity: O(n) [for stack].

Problem-24

HÌnh chữ nhật lớn nhất trong biểu đồ: Biểu đồ là một đa giác bao gồm một chuỗi các hình chữ nhật được căn chỉnh tại một đường cơ sở chung. Để đơn giản, giả sử rằng các hình chữ nhật có chiều rộng bằng nhau nhưng có thể có chiều cao khác nhau. Ví dụ: hình bên trái cho thấy một biểu đồ bao gồm các hình chữ nhật với các chiều cao 3, 2, 5, 6, 1, 4, 4, được đo bằng đơn vị trong đó 1 là chiều rộng của các hình chữ nhật.

Cho một mảng có chiều cao là các hình chữ nhật (giả sử chiều rộng là 1), chúng ta cần tìm hình chữ nhật lớn nhất có thể. Đối với ví dụ đã cho, hình chữ nhật lớn nhất là phần được gạch chéo.

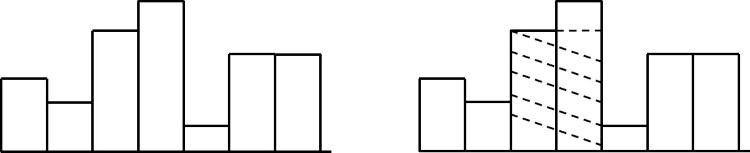
Solution: Một câu trả lời đơn giản là đi đến từng thanh trong biểu đồ và tìm diện tích tối đa có thể có trong biểu đồ cho nó. Cuối cùng, hãy tìm giá trị tối đa của các giá trị này. Điều này sẽ yêu cầu $O (n^2)$.

Problem-25

Có thể cải thiện time complexity của Problem-24 không?

Solution: Yes, bằng cách tìm kiếm tuyến tính sử dụng một stack các bài toán con chưa hoàn chỉnh. Nghe hơi khó hiểu, để mình giải thích chi tiết hơn.
Problem-24 này có rất nhiều cách để giải quyết. Judge đã đưa ra một thuật toán hay cho vấn đề này dựa trên ngăn xếp.
Chúng ta xử lý các phần tử theo thứ tự từ trái sang phải và duy trì một stack thông tin về các biểu đồ con đã bắt đầu nhưng chưa hoàn thành.
Nếu ngăn xếp trống, hãy mở một bài toán con mới bằng cách đẩy phần tử lên ngăn xếp. Nếu không, hãy so sánh nó với phần tử ở trên cùng của ngăn xếp.
Nếu cái mới lớn hơn hoặc bằng, chúng tôi lại push nó vào stack. Trong tất cả những trường hợp này, chúng ta tiếp tục với phần tử mới tiếp theo.
Nếu phần tử mới nhỏ hơn, chúng ta hoàn thành bài toán con trên cùng bằng cách cập nhật vùng tối đa đối với phần tử ở trên cùng của ngăn xếp. Sau đó, chúng ta loại bỏ phần tử ở trên cùng và lặp lại quy trình giữ phần tử mới hiện tại.
Bằng cách này, tất cả các bài toán con được kết thúc khi ngăn xếp trở nên trống hoặc phần tử trên cùng của nó nhỏ hơn hoặc bằng phần tử mới, dẫn đến các hành động được mô tả ở trên.
Nếu tất cả các phần tử đã được xử lý và ngăn xếp vẫn chưa trống, chúng ta sẽ hoàn thành các bài toán con còn lại bằng cách cập nhật vùng tối đa đối với các phần tử ở trên cùng.\

	public static int maxRetangleArea(int[] A) {
		Stack<Integer> s = new Stack<Integer>();
		if(A == null || A.length == 0) {
			return 0;
		}
		// Initialize max area
		int maxArea = 0;
		int i = 0;
		//run through all bars of given histogram
		while(i < A.length) {
			//If current bar is higher than the bar of the stack peek, push it to stack
			if(s.empty() || A[s.peek()] <= A[i]) {
				s.push(i++);
				System.out.println(s);
			} else {
				System.out.print(s);
				//if current bar is lower than the stack peek
				//calculate area of rectangle with stack top as the smallest bar.
				//'i' is 'right index' for the top and element before top in stack is 'left index'
				int top = s.pop();
				System.out.print(" ------ i:" + i + " ---- top: " + top + " ---- maxArea: " + maxArea);
				//calculate the area with A[top] stack as smallest bar and update maxArea if needed
				maxArea = Math.max(maxArea, A[top]*(s.empty()?i:(i - s.peek() - 1)));
				System.out.print(" ---- calculate:" + A[top]*(s.empty()?i:(i - s.peek() - 1)));
				System.out.println();
			}
		}
		
		//Now pop the remaining bars from stack and calculate area with every popped bar as the smallest bar.
		while(!s.isEmpty()) {
			System.out.println();
			System.out.print(s);
			int top = s.pop();
			System.out.print(" ---- top: " + top + " ---- maxArea: " + maxArea);
			maxArea = Math.max(maxArea, A[top]*(s.empty()?i:(i - s.peek() - 1)));
			System.out.print(" ---- calculate1:" + A[top]*(s.empty()?i:(i - s.peek() - 1)));
		}
		
		return maxArea;
	}
	
	public static void main(String[] args) {
		int[] A = {3,2,5,6,1,4,4};
		System.out.println("\nResult: " + maxRetangleArea(A));
	}

Giải thuật này khá khó hiểu nếu bạn chỉ đọc lướt qua và không xem kỹ, code mình có thêm một số lệnh in kết quả ra console để tiện theo dõi giải thuật, các bạn có thể thử cho riêng mình 😁

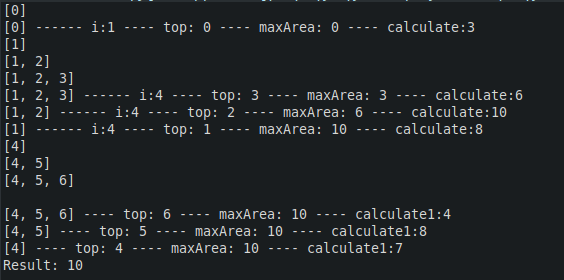
Nếu xem qua, giải pháp này có vẻ có độ phức tạp $O(n^2)$. Nhưng nếu chúng ta xem xét cẩn thận, mọi phần tử được push và pop nhiều nhất một lần, và trong mỗi bước của hàm ít nhất một phần tử được push hoặc pop.
Vì khối lượng công việc cho các quyết định và cập nhật là không đổi, độ phức tạp của thuật toán là $O (n)$ theo phân tích khấu hao.
Space Complexity: O(n) [for stack].

Problem-26

Đưa ra giải thuật sắp xếp ngăn xếp theo thứ tự tăng dần.

Solution:

	public static Stack<Integer> sort(Stack<Integer> stk){
		Stack<Integer> rstk = new Stack<Integer>();
		while(!stk.isEmpty()) {
			int tmp = stk.pop();
			while(!rstk.isEmpty() && rstk.peek() > tmp) {
				stk.push(rstk.pop());
			}
			rstk.push(tmp);
		}
		return rstk;
	}

Time Complexity: $O(n^2)$. Space Complexity: $O(n)$, for stack.

Problem27

Cho một chồng số nguyên, làm cách nào để bạn kiểm tra xem từng cặp số liên tiếp trong ngăn xếp có liên tiếp hay không.
Các cặp có thể tăng hoặc giảm và nếu ngăn xếp có số phần tử lẻ, thì phần tử ở trên cùng sẽ bị loại ra khỏi một cặp.
Ví dụ: nếu chồng các phần tử là [4, 5, -2, -3, 11, 10, 5, 6, 20], thì kết quả đầu ra phải là true vì mỗi cặp (4, 5), (- 2, -3), (11, 10), và (5, 6) bao gồm các số liên tiếp.

Solution: Mình sẽ trình bày chi tiết trong chương Queues.

Problem-28

Cho một mảng số, loại bỏ các số trùng lặp liền kề. Output là một mảng không có bất kì bản sao liền kề nào.

Solution: Giải pháp này hoạt động với khái niệm về in-place stack. Khi phần tử trên ngăn xếp không khớp với số hiện tại, chúng ta thêm phần tử đó vào ngăn xếp. Khi nó khớp với đỉnh ngăn xếp, chúng tôi bỏ qua các số cho đến khi phần tử khớp với đỉnh ngăn xếp và xóa phần tử khỏi ngăn xếp.

	public int removeAdjacentDuplicates(int A[]) {
		int stkptr = -1;
		int i = 0;
		while(i < A.length) {
			if(stkptr == -1 || A[stkptr] != A[i]) {
				stkptr++;
				A[stkptr] = A[i];
				i++;
			} else {
				while(i < A.length && A[stkptr] == A[i]) {
					i++;
				}
				stkptr--;
			}
		}
		return stkptr;
	}

Time Complexity: $O(n)$. Space Complexity: $O(1) $

Problem-29

Nếu ngăn xếp quá lớn, nó có thể bị mất cân bằng. Trong cuộc sống thực, chúng ta có thể sẽ bắt đầu một ngăn xếp mới khi ngăn xếp trước đó vượt quá một số ngưỡng.
Triển khai cấu trúc dữ liệu bắt chước điều này và bao gồm một số ngăn xếp và sẽ tạo một ngăn xếp mới khi ngăn xếp trước đó vượt quá dung lượng.
push() và pop() của lớp này sẽ hoạt động giống hệt như một ngăn xếp thông thường.

Solution:

class StackForStackSets{
	private int top = -1;
	private int[] arr;
	
	//Maximum size of stack
	private int capacity;
	public StackForStackSets(int capacity) {
		this.capacity = capacity;
		arr = new int[capacity];
	}
	
	public void push(int v) {
		arr[++top] = v;
	}
	
	public int pop() {
		return arr[top--];
	}
	
	//if the stack is at capacity
	public boolean isAtCapacity() {
		return capacity == top +1;
	}
	
	//return the size of the stack
	public int size() {
		return top+1;
	}
	
	public String toString() {
		String s = "";
		int index = top;
		while(index >= 0) {
			s += "[" + arr[index--] + "]" + " --> ";
		}
		return s;
	}
}

public class StackSets {
	//Number of elements for each stack
	private int threshold;
	private ArrayList<StackForStackSets> listOfStacks = new ArrayList<>();
	
	public StackSets(int threshold) {
		this.threshold = threshold;
	}
	
	//get the last stack
	public StackForStackSets getLastStack() {
		int size = listOfStacks.size();
		if(size <= 0)	
			return null;
		else return listOfStacks.get(size - 1);
	}
	
	public StackForStackSets getNthStack(int n) {
		int size = listOfStacks.size();
		if(size <= 0)
			return null;
		else return listOfStacks.get(n-1);
	}
	
	//push value
	public void push(int value) {
		StackForStackSets lastStack = this.getLastStack();
		if(lastStack == null) {
			lastStack = new StackForStackSets(threshold);
			lastStack.push(value);
			listOfStacks.add(lastStack);
		} else {
			if(!lastStack.isAtCapacity()) {
				lastStack.push(value);
			} else {
				StackForStackSets newLastStack = new StackForStackSets(threshold);
				newLastStack.push(value);
				listOfStacks.add(newLastStack);
			}
		}
	}
	
	//the pop
	public int pop() {
		StackForStackSets lastStack = this.getLastStack();
		int v = lastStack.pop();
		if(lastStack.size() == 0) {
			listOfStacks.remove(listOfStacks.size() - 1);
		}
		return v;
	}
	
	//pop from the nth stack
	public int pop(int nth) {
		StackForStackSets nthStack = this.getNthStack(nth);
		int v = nthStack.pop();
		if(nthStack.size() == 0) {
			listOfStacks.remove(listOfStacks.size() - 1);
		}
		return v;
	}
	
	public String toString() {
		String s = "";
		for (int i = 0; i < listOfStacks.size(); i++) {
			StackForStackSets stack = listOfStacks.get(i);
			s = "Stack " + i + ": " + stack.toString() + s;
		}
		return s;
	}
}