11.1 Searching(Tìm kiếm) là gì?

Trong khoa học máy tính, tìm kiếm là quá trình tìm một phần tử với các thuộc tính được xác định từ một tập hợp các phần tử. Các phần tử có thể được lưu trữ dưới dạng bản ghi trong cơ sở dữ liệu, thành phần dữ liệu đơn giản trong mảng, văn bản trong tệp, nút trong cây, đỉnh và cạnh trong biểu đồ hoặc chúng có thể là thành phần của không gian tìm kiếm khác.

11.2 Tại sao chúng ta cần Searching?

Tìm kiếm là một trong những thuật toán khoa học máy tính cốt lõi. chúng ta biết rằng máy tính ngày nay lưu trữ rất nhiều thông tin. Để truy xuất thông tin này một cách thành thạo, chúng ta cần các thuật toán tìm kiếm rất hiệu quả.

Có một số cách tổ chức dữ liệu giúp cải thiện quá trình tìm kiếm. Điều đó có nghĩa là, nếu chúng ta sắp xếp dữ liệu theo đúng thứ tự, thì sẽ dễ dàng tìm kiếm phần tử được yêu cầu. Sắp xếp là một trong những kỹ thuật để sắp xếp các phần tử theo thứ tự. Trong chương này chúng ta sẽ thấy các thuật toán tìm kiếm khác nhau.

11.3 Phân loại Searching

Sau đây là các loại tìm kiếm mà chúng ta sẽ thảo luận trong cuốn sách này.

• Tìm kiếm tuyến tính không có thứ tự
• Tìm kiếm tuyến tính được sắp xếp/có thứ tự
• Tìm kiếm nhị phân
• Symbol Tables and Hashing
• Các thuật toán tìm kiếm chuỗi: Tries, Ternary Search và Suffix Trees

11.4 Tìm kiếm tuyến tính không có thứ tự

Giả sử chúng ta được cung cấp một mảng không biết thứ tự của các phần tử. Điều đó có nghĩa là các phần tử của mảng không được sắp xếp. Trong trường hợp này, để tìm kiếm một phần tử, chúng ta phải quét toàn bộ mảng và xem liệu phần tử đó có trong danh sách đã cho hay không.

    public int UnorderdLinearSearch(int[] A, int data){
        for(int i = 0; i < A.length; i++){
            if(A[i] == data){
                return i;
            }
        }
        return -1;
    }

Time complexity: O(n), trong trường hợp xấu nhất, chúng ta cần quét toàn bộ mảng. Space complexity: O(1).

11.5 Tìm kiếm tuyến tính được sắp xếp/có thứ tự

Nếu các phần tử của mảng đã được sắp xếp sẵn thì trong nhiều trường hợp chúng ta không cần phải quét toàn bộ mảng để xem phần tử đó có trong mảng đã cho hay không. Trong thuật toán dưới đây, có thể thấy rằng, tại một thời điểm bất kỳ nếu giá trị tại $A[i]$ lớn hơn dữ liệu cần tìm thì ta chỉ cần trả về –1 mà không cần tìm mảng còn lại.

Time complexity: O(n) Điều này là do trong trường hợp xấu nhất, chúng ta cần quét toàn bộ mảng. Nhưng trong trường hợp trung bình, nó làm giảm độ phức tạp mặc dù growth rate là như nhau.
Space complexity: O(1).

Note: Đối với thuật toán trên, chúng ta có thể cải thiện hơn nữa bằng cách tăng chỉ số với tốc độ nhanh hơn (giả sử, 2). Điều này sẽ làm giảm số lần so sánh để tìm kiếm trong danh sách đã sắp xếp.

11.6 Binary Search

Chúng ta hãy xem xét vấn đề tìm kiếm một từ trong từ điển. Thông thường, chúng ta trực tiếp truy cập một số trang gần đúng [giả sử, trang giữa] và bắt đầu tìm kiếm từ điểm đó. Nếu tên mà chúng ta đang tìm kiếm giống nhau thì quá trình tìm kiếm đã hoàn tất. Nếu trang nằm trước các trang đã chọn thì áp dụng quy trình tương tự cho nửa đầu; mặt khác, áp dụng quy trình tương tự cho nửa thứ hai. Binary search cũng hoạt động theo cách tương tự. Thuật toán áp dụng chiến lược như vậy được gọi là binary search algorithm(thuật toán tìm kiếm nhị phân).

    //Phiên bản vòng lặp
    public int BinarySearchIterative(int[] A, int data){
        int low = 0, high = A.length-1, mid;
        while (low <= high) {
            mid = low + (high - low)/2;
            if(A[mid] == data){
                return mid;
            } else if (A[mid] < data) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        return -1;
    }

    //Phiên bản đệ quy
    public int BinarySearchRecursive(int[] A, int low, int high, int data){
        int mid = low + (high -low)/2;
        if (low > high) {
            return -1;
        }
        if (A[mid] == data){
            return mid;
        } else if (A[mid] < data) {
            return BinarySearchRecursive(A, mid+1, high, data);
        } else {
            return BinarySearchRecursive(A, low, mid-1, data);
        }
    }

Sự đệ quy cho tìm kiếm nhị phân là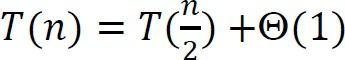

Điều này là bởi vì chúng ta luôn luôn chỉ xem xét một nửa danh sách đầu vào và loại bỏ nửa còn lại. Sử dụng Divide and Conquer master theorem ta được, $T(n) = O(logn)$.

Time Complexity: O(logn).
Space Complexity: O(1) (Đối với iterative algorithm)

11.7 Interpolation Search(Tìm kiếm nội suy)

Không còn nghi ngờ gì nữa, tìm kiếm nhị phân là một thuật toán tuyệt vời để tìm kiếm với độ phức tạp thời gian chạy trung bình của $O(logn)$. Nó luôn chọn phần giữa của không gian tìm kiếm còn lại, loại bỏ một nửa hoặc nửa kia, một lần nữa tùy thuộc vào sự so sánh giữa giá trị khóa được tìm thấy ở vị trí ước tính (ở giữa) và giá trị khóa được tìm kiếm. Không gian tìm kiếm còn lại được giảm xuống một phần trước hoặc sau vị trí ước tính.

Trong toán học, Interpolation(phép nội suy) là một quá trình xây dựng các điểm dữ liệu mới trong phạm vi của một tập hợp rời rạc các điểm dữ liệu đã biết. Trong khoa học máy tính, người ta thường có một số điểm dữ liệu đại diện cho các giá trị của một hàm cho một số lượng giới hạn các giá trị của biến độc lập.

Nó thường được yêu cầu để nội suy (tức là ước lượng) giá trị của hàm đó đối với một giá trị trung gian của biến độc lập. Ví dụ, giả sử chúng ta có một bảng như thế này, cho một số giá trị của một hàm f chưa biết. Phép nội suy cung cấp một phương tiện ước tính hàm tại các điểm trung gian, chẳng hạn như x = 55.

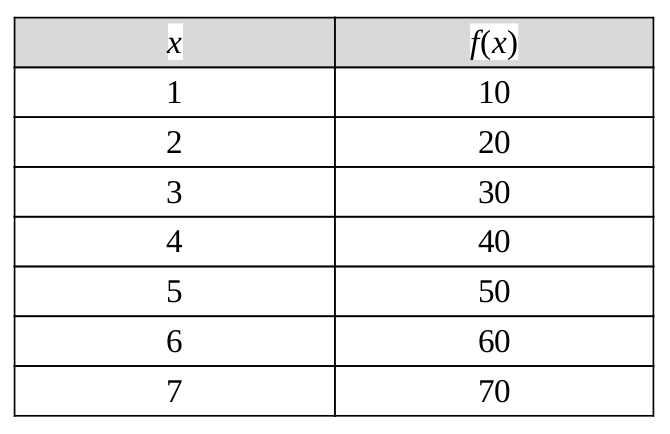
Có nhiều phương pháp nội suy khác nhau, và một trong những phương pháp đơn giản nhất là nội suy tuyến tính. Vì 55 nằm ở khoảng giữa của 50 và 60, nên sẽ hợp lý khi lấy 55 ở khoảng giữa của f(5) = 50 và f(6) = 60, cho kết quả là 55.

Phép nội suy tuyến tính lấy hai điểm dữ liệu, giả sử $(x1; y2)$ và $(x2, y2)$ và phép nội suy được cho bởi:

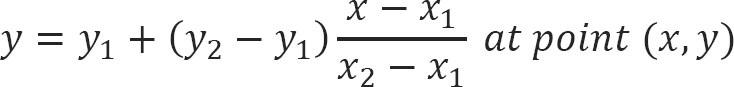
Với các đầu vào ở trên, điều gì sẽ xảy ra nếu chúng ta không sử dụng hằng số ½ mà dùng một hằng số khác chính xác hơn là “K”, có thể đưa chúng ta đến gần mục được tìm kiếm hơn.

Thuật toán này cố gắng làm theo cách chúng ta tìm kiếm tên trong danh bạ điện thoại hoặc một từ trong từ điển. Chúng ta, con người, biết trước rằng trong trường hợp tên mà chúng ta đang tìm bắt đầu bằng chữ “m”, chẳng hạn như “monk”, chúng ta nên bắt đầu tìm kiếm ở gần giữa danh bạ điện thoại.

Vì vậy, nếu chúng ta đang tìm kiếm từ "career(nghề nghiệp)" trong từ điển, bạn sẽ biết rằng nó nên được đặt ở đâu đó ngay từ đầu. Điều này là do chúng ta biết thứ tự của các chữ cái, chúng ta biết khoảng (a-z) và bằng cách nào đó, bằng trực giác, chúng ta biết rằng các từ được phân tán như nhau. Những sự thật này đủ để nhận ra rằng tìm kiếm nhị phân có thể là một lựa chọn tồi. Thật vậy, thuật toán tìm kiếm nhị phân chia danh sách thành hai danh sách con bằng nhau, điều này là vô ích nếu chúng ta biết trước rằng mục được tìm kiếm nằm ở đâu đó ở đầu hoặc cuối danh sách.

Thuật toán tìm kiếm nội suy cố gắng cải thiện tìm kiếm nhị phân. Câu hỏi là làm thế nào để tìm thấy giá trị này? Chà, chúng ta biết giới hạn của khoảng và nhìn kỹ hơn vào hình ảnh trên, chúng ta có thể xác định công thức sau.

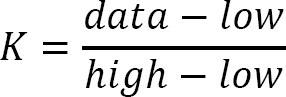
Hằng số K này được sử dụng để thu hẹp không gian tìm kiếm. Đối với tìm kiếm nhị phân, hằng số K này là $(low + high)/2$.

Bây giờ chúng ta có thể chắc chắn rằng chúng ta đang tiến gần hơn đến giá trị được tìm kiếm. Tính trung bình, tìm kiếm nội suy tạo ra các phép so sánh $log (logn)$ (nếu các phần tử được phân phối đồng đều), trong đó n là số lượng phần tử được tìm kiếm. Trong trường hợp xấu nhất (ví dụ khi các giá trị số của các phần tử tăng theo cấp số nhân), nó có thể tạo ra các phép so sánh O(n).

Trong interpolation-sequential search(tìm kiếm tuần tự nội suy), phép nội suy được sử dụng để tìm một mục gần mục đang được tìm kiếm, sau đó tìm kiếm tuyến tính được sử dụng để tìm mục chính xác. Để thuật toán này cho kết quả tốt nhất, tập dữ liệu phải được sắp xếp theo thứ tự và phân bổ đồng đều.

    public static int interpolationSearch(int[] A, int data){
        int low = 0, high = A.length-1, mid;
        while (A[low] <= data && A[high] >= data) {
            if(A[high] - A[low] == 0){
                return (low + high)/2;
            }
            mid = low +
                    ((data - A[low]) * (high - low)) / (A[high] - A[low]);
            if(A[mid] < data){
                low = mid + 1;
            } else if (A[mid] > data) {
                high = mid - 1;
            } else {
                return mid;
            }
        }

        if(A[low] == data){
            return low;
        } else {
            return -1;
        }
    }

11.8 So sánh các thuật toán tìm kiếm cơ bản

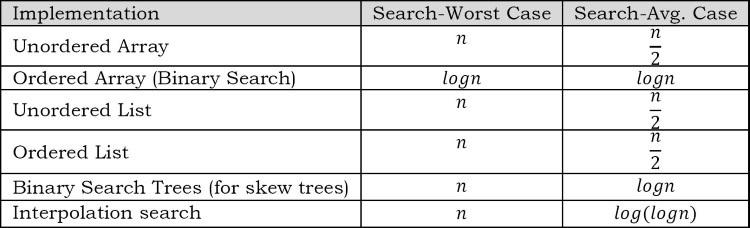
Lưu ý: Để xem lại về cây tìm kiếm nhị phân, các bạn có thể xem lại bài viết này Tree.

11.9 Symbol Tables and Hashing

Mình sẽ trình bày chi tiết khi tới chương Symbol Tables and Hashing

11.10 String Searching Algorithms

Mình sẽ trình bày chi tiết khi tới chương String Algorithms