Chương 6: TREES - 1. Tree là gì? Lý thuyết về Binary Tree.

6.1 What is a Tree?

Tree là một cấu trúc dữ liệu tương tự như một linked list nhưng thay vì mỗi node chỉ đơn giản chỉ đến node tiếp theo theo kiểu tuyến tính, ở tree mỗi node trỏ đến một số node khác. Tree là một ví dụ về cấu trúc dữ liệu phi tuyến. Cấu trúc cây là một cách thể hiện bản chất thứ bậc của cấu trúc dưới dạng đồ họa.

Trong tree ADT (Abstract Data Type), thứ tự của các phần tử không quan trọng. Nếu chúng ta cần thông tin đặt hàng, cấu trúc dữ liệu tuyến tính như danh sách liên kết, ngăn xếp, hàng đợi, v.v. có thể được sử dụng.

6.2 Glossary(Bảng chú giải thuật ngữ)

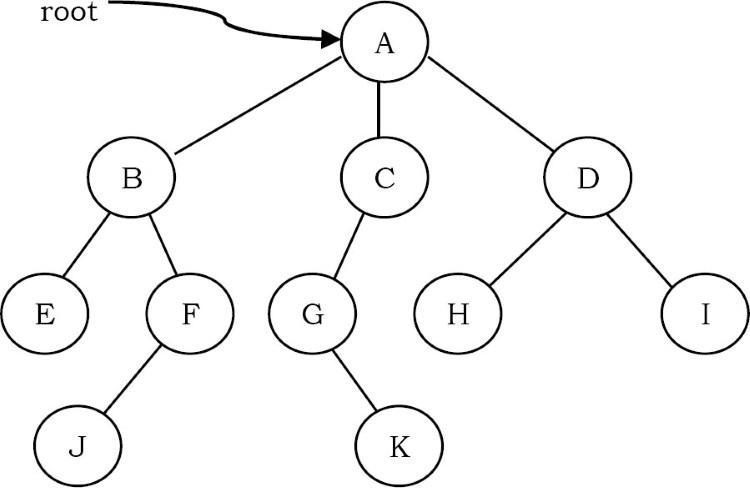
• Root của cây là node không có bố mẹ. Có thể có nhiều nhất một node gốc trong một cây (node A trong ví dụ trên).
• Một edge(cạnh) đề cập đến liên kết từ cha đến con (tất cả các liên kết trong hình).
• Một node không có node con được gọi là leaf node (E, J, K, H và I).
• Những node con có cùng node cha được gọi là siblings(anh chị em ruột - B, C, D là siblings của A và E, F là anh chị em của B).
• Một node p là ancestor(tổ tiên) của node q nếu tồn tại một đường đi từ gốc đến q và p xuất hiện trên đường đi. Node q được gọi là descendant(con cháu) của p. Ví dụ, A, C và G là tổ tiên của K.
• Tập hợp tất cả các node ở một độ sâu nhất định được gọi là level của cây (B, C và D là cùng một mức). Nút Root ở mức không.
• Độ sâu của node là độ dài của đường đi từ gốc đến node (độ sâu của G là 2, A - C - G).
• Chiều cao của một node là độ dài của đường đi từ nút đó đến nút sâu nhất. Chiều cao của cây là chiều dài của đường đi từ root đến node sâu nhất trong cây. Một cây chỉ có một node (gốc) có chiều cao bằng không. Trong ví dụ trước, chiều cao của B là 2 (B - F - J).
• Chiều cao của cây là chiều cao lớn nhất trong số tất cả các nút trong cây và chiều sâu của cây là chiều sâu lớn nhất trong số tất cả các nút trong cây. Đối với một cây nhất định, chiều sâu và chiều cao trả về cùng một giá trị. Nhưng đối với các node riêng lẻ, chúng ta có thể nhận được các kết quả khác nhau.

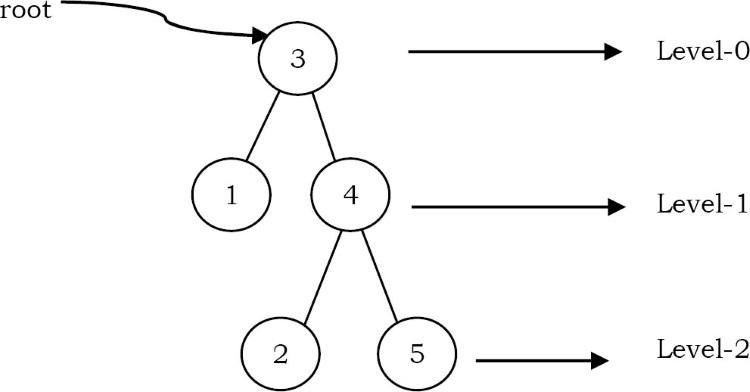
• Kích thước của một node là số lượng nút con mà nó có bao gồm cả chính nó (kích thước của cây con C là 3).
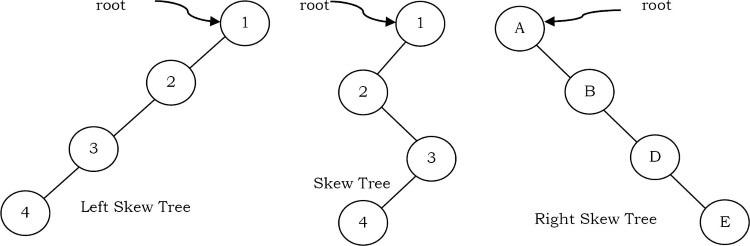
• Nếu mọi node trong cây chỉ có một node con (trừ các nút lá) thì ta gọi các cây như vậy là cây xiên(skew trees). Nếu mọi node chỉ có con trái thì chúng ta gọi chúng là cây xiên trái(left skew trees). Tương tự, nếu mọi node chỉ có con bên phải thì chúng ta gọi chúng là cây xiên bên phải(right skew trees).

6.3 Binary Trees

Một cây được gọi là cây nhị phân(binary tree) nếu mỗi nút không có con nào, một con hoặc hai con. Cây rỗng cũng là một cây nhị phân hợp lệ. Chúng ta có thể hình dung cây nhị phân bao gồm một gốc và hai cây nhị phân rời rạc, được gọi là cây con trái và phải của gốc.

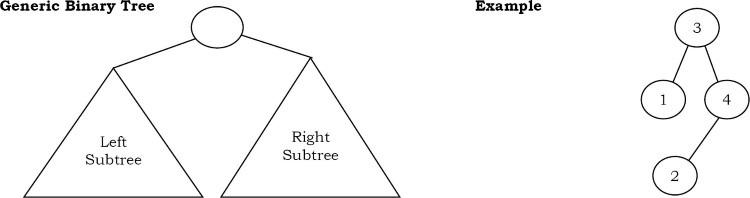
Types of Binary Trees

Strict Binary Tree: Cây nhị phân được gọi là cây nhị phân nghiêm ngặt(Strict Binary Tree) nếu mỗi nút có đúng hai nút con hoặc không có nút con nào.

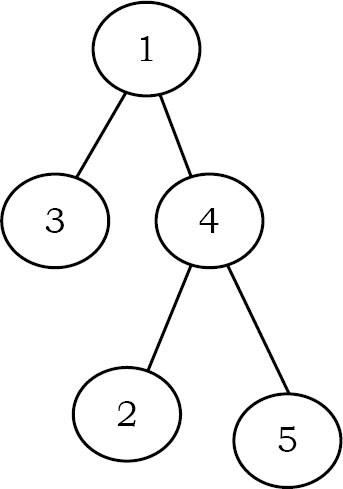
Full Binary Tree: Cây nhị phân được gọi là cây nhị phân đầy đủ(Full Binary Tree) nếu mỗi nút có đúng hai nút con và tất cả các nút lá đều ở cùng một mức.

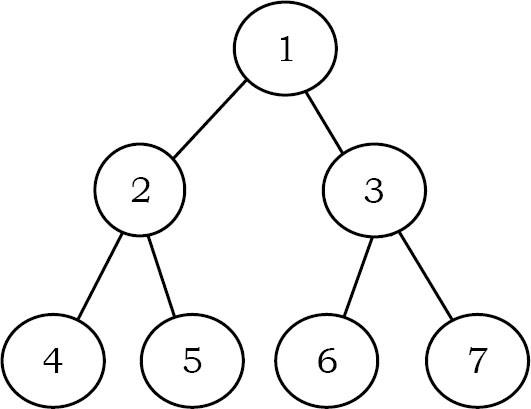
Complete Binary Tree: Trước khi xác định cây nhị phân hoàn chỉnh(Complete Binary Tree), chúng ta hãy giả sử rằng chiều cao của cây nhị phân là h. Trong cây nhị phân hoàn chỉnh, nếu chúng ta đánh số cho các nút bằng cách bắt đầu từ gốc (giả sử nút gốc có 1) thì chúng ta sẽ nhận được một chuỗi hoàn chỉnh từ 1 đến số nút trong cây.

Trong khi đi ngang, chúng ta cũng nên đánh số cho các con trỏ NULL. Cây nhị phân được gọi là cây nhị phân hoàn chỉnh nếu tất cả các nút lá ở độ cao h hoặc h - 1 và cũng không thiếu bất kỳ số nào trong dãy tuần tự.

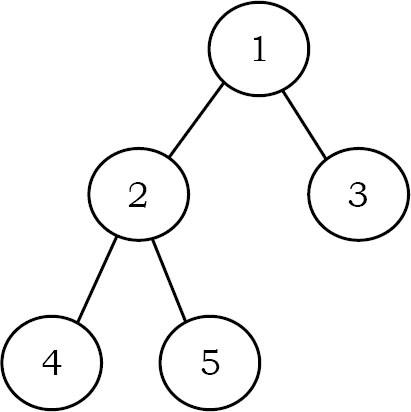
Properties of Binary Trees

Đối với các tính chất sau, chúng ta hãy giả sử rằng chiều cao của cây là h. Ngoài ra, giả sử rằng nút gốc ở độ cao bằng không.

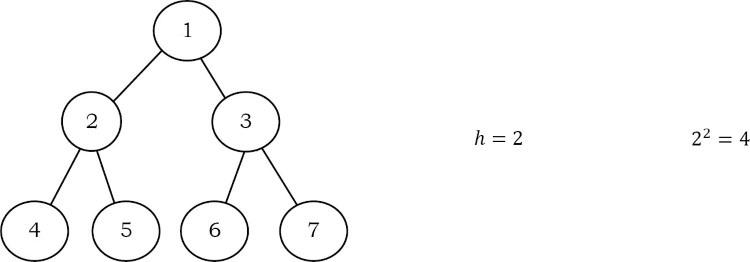
Từ sơ đồ dưới đây, chúng ta có thể suy ra các thuộc tính sau:

• Số nút n trong cây nhị phân đầy đủ là $2 ^ { h + 1 } - 1$. Vì có h mức, chúng ta cần cộng tất cả các nút ở mỗi cấp $[2 ^ { 0 } + 2 ^ { 1 } + 2 ^ { 2 } + \ldots + 2 ^ { h } = 2 ^ { h + 1 } - 1]$.
• Số nút n trong một cây nhị phân hoàn chỉnh nằm trong khoảng từ $2^h$ (tối thiểu) đến $2 ^ { h + 1 } - 1$ (tối đa). Mình sẽ nói thêm chi tiết về cái này trong chương về Priority Queue.
• Số lượng nút lá trong một cây nhị phân đầy đủ là $2^h$.
• Số liên kết NULL (con trỏ lãng phí) trong một cây nhị phân hoàn chỉnh có $n$ node là $n + 1$.

Structure of Binary Trees

Bây giờ chúng ta hãy xác định cấu trúc của cây nhị phân. Để đơn giản, giả sử rằng dữ liệu của các nút là số nguyên. Một cách để biểu diễn một node (chứa dữ liệu) là có hai liên kết trỏ đến nút con bên trái và bên phải cùng với các trường dữ liệu như được hiển thị bên dưới:

public class BinaryTreeNode {
	public int data;
	public BinaryTreeNode left, right;

	public BinaryTreeNode(int data) {
		this.data = data;
		left = null;
		right = null;
	}

	public int getData() {
		return data;
	}

	public void setData(int data) {
		this.data = data;
	}

	public BinaryTreeNode getLeft() {
		return left;
	}

	public void setLeft(BinaryTreeNode left) {
		this.left = left;
	}

	public BinaryTreeNode getRight() {
		return right;
	}

	public void setRight(BinaryTreeNode right) {
		this.right = right;
	}
}

Lưu ý: Trong cây, luồng mặc định là từ cha đến con và không bắt buộc phải hiển thị các nhánh có hướng. Đối với phần này, chúng ta giả định rằng cả hai đại diện được hiển thị bên dưới đều giống nhau.

Operations on Binary Trees

Basic Operations

• Thêm một phần tử vào cây
• Xóa một phần tử khỏi cây
• Tìm kiếm trong cây
• Duyệt cây

Auxiliary(phụ trợ) Operations

• Tìm kích thước của cây
• Tìm chiều cao của cây
• Tìm cấp có tổng tối đa
• Tìm tổ tiên chung gần nhất (the least common ancestor - LCA) cho một cặp nút nhất định và nhiều nút khác.

Một số ứng dụng của Binary Trees

Sau đây là một số ứng dụng mà cây nhị phân đóng một vai trò quan trọng:

• Cây biểu thức(Expression trees) được sử dụng trong trình biên dịch.
• Cây mã hóa Huffman được sử dụng trong các thuật toán nén dữ liệu.
• Cây tìm kiếm nhị phân (Binary Search Tree - BST), hỗ trợ tìm kiếm, chèn và xóa trên một tập hợp các mục trong $O (logn)$ (trung bình).
• Priority Queue (PQ), hỗ trợ tìm kiếm và xóa tối thiểu (hoặc tối đa) trên một collection các mục theo thời gian logarit (trong trường hợp xấu nhất).