Chương 4: STACKS - Problems & Solutions(01-14)

Problem-1

Thảo luận về cách có thể sử dụng ngăn xếp để kiểm tra balancing of symbols.

Solution: Ngăn xếp có thể được sử dụng để kiểm tra xem biểu thức đã cho có các ký hiệu cân bằng hay không.
Thuật toán này rất hữu ích trong trình biên dịch. Mỗi lần bộ phân tích cú pháp đọc một ký tự tại một thời điểm. Nếu ký tự là một dấu phân cách mở như (, {, hoặc [thì nó được ghi vào ngăn xếp. Khi gặp phải dấu phân cách đóng như),} hoặc] thì ngăn xếp sẽ xuất hiện. Các dấu phân cách mở và đóng sau đó được so sánh. Nếu chúng khớp nhau, quá trình phân tích cú pháp của chuỗi sẽ tiếp tục. Nếu chúng không khớp, trình phân tích cú pháp chỉ ra rằng có lỗi trên dòng. Thuật toán O (n) thời gian tuyến tính dựa trên ngăn xếp có thể được đưa ra như sau:

Algorithm

1. Tạo một ngăn xếp.
2. while (Chưa tới cuối của input)
   • 2.1 Nếu ký tự được đọc không phải là ký hiệu cần cân bằng, hãy bỏ qua nó.
   • 2.2 Nếu ký tự là một ký hiệu mở như (, [, {, hãy đẩy nó lên ngăn xếp
   • 2.3 Nếu nó là một ký hiệu đóng như),],}, thì nếu ngăn xếp trống sẽ báo lỗi. Nếu không, pop ngăn xếp đó.
   • 2.4 Nếu biểu tượng pop ra không phải là biểu tượng mở tương ứng, hãy báo lỗi.
3. Khi kết thúc input, nếu ngăn xếp không trống, báo lỗi

Để tracing thuật toán, chúng ta hãy giả sử rằng đầu vào là: () (() [()])

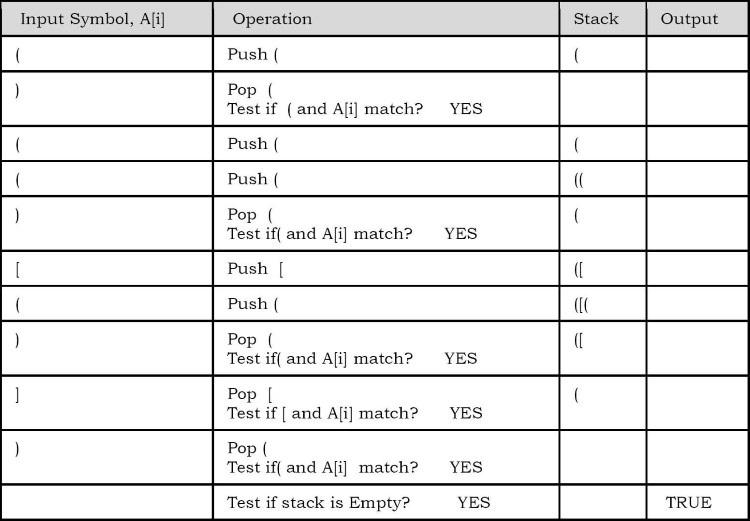
Time Complexity: O(n). Vì chúng ta quét input chỉ 1 lần.
Space Complexity: O(n) Do sử dụng Stack.

	public boolean isValidSymbolPattern(String s) {
		Stack<Character> stk = new Stack<>();
		if(s == null || s.length() == 0) {
			return true;
		}
		for(int i = 0; i < s.length(); i++) {
			if(s.charAt(i) == ')') {
				if(!stk.isEmpty() && stk.peek() == ')') {
					stk.pop();
				}else {
					return false;
				}
			}else if(s.charAt(i) == ']') {
				if(!stk.isEmpty() && stk.peek() == '[') {
					stk.pop();
				}else {
					return false;
				}
			}else if(s.charAt(i) == '{') {
				if(!stk.isEmpty() && stk.peek() == '}') {
					stk.pop();
				}else {
					return false;
				}
			}else {
				stk.push(s.charAt(i));
			}
		}
		
		if(stk.isEmpty()) {
			return true;
		}else {
			return false;
		}
	}

Problem-2

Thảo luận về thuật toán chuyển đổi infix sang postfix bằng cách sử dụng ngăn xếp.

Solution: Trước khi thảo luận về thuật toán, trước tiên chúng ta hãy xem định nghĩa của các biểu thức infix, prefix và postfix.

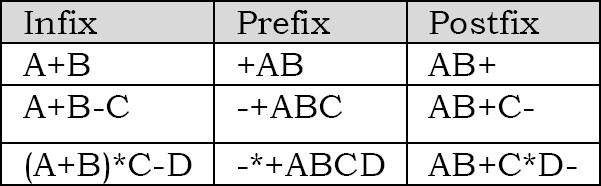
Infix: Biểu thức infix là một ký tự đơn hoặc một toán tử, được tiến hành bởi một chuỗi infix và theo sau là một chuỗi Infix khác.

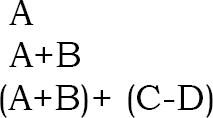
Prefix: Biểu thức tiền tố là một ký tự đơn hoặc một toán tử, theo sau là hai chuỗi tiền tố. Mọi chuỗi tiền tố dài hơn một biến đơn chứa một toán tử, toán hạng thứ nhất và toán hạng thứ hai.

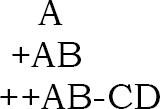
Postfix: Một biểu thức hậu tố (còn được gọi là Ký hiệu đánh bóng ngược) là một ký tự đơn hoặc một toán tử, đứng trước hai chuỗi hậu tố. Mỗi chuỗi hậu tố dài hơn một biến đơn chứa các toán hạng đầu tiên và thứ hai theo sau bởi một toán tử.

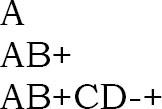
Các khái niệm tiền tố và hậu tố là các phương pháp viết biểu thức toán học không có dấu ngoặc đơn. Thời gian để đánh giá một hậu tố và biểu thức tiền tố là O (n), n là số phần tử trong mảng.

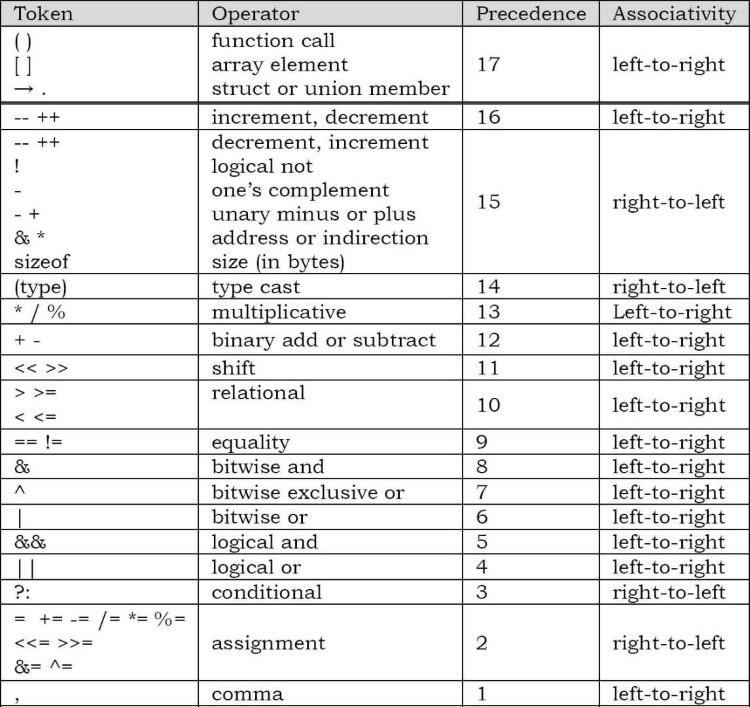
Bây giờ, chúng ta hãy tập trung vào thuật toán. Trong các biểu thức infix, ưu tiên toán tử là ngầm định trừ khi chúng ta sử dụng dấu ngoặc đơn. Do đó, đối với thuật toán chuyển đổi tiền tố sang hậu tố, chúng ta phải xác định độ ưu tiên của toán tử (hoặc mức độ ưu tiên) bên trong thuật toán. Bảng cho thấy mức độ ưu tiên và tính liên kết của chúng (thứ tự đánh giá) giữa các toán tử.

Các tính chất quan trọng:

• Chúng ta hãy xem xét biểu thức infix 2 + 3 * 4 và hậu tố tương đương của nó 2 3 4 * +. Lưu ý rằng giữa infix và postfix, thứ tự của các số (hoặc toán hạng) là không thay đổi. Nó là 2 3 4 trong cả hai trường hợp. Nhưng thứ tự của các toán tử * và + bị ảnh hưởng trong hai biểu thức.
• Chỉ một ngăn xếp là đủ để chuyển đổi một biểu thức infix thành biểu thức hậu tố. Ngăn xếp mà chúng ta sử dụng trong thuật toán sẽ được sử dụng để thay đổi thứ tự của các toán tử từ infix sang postfix. Ngăn xếp mà chúng ta sử dụng sẽ chỉ chứa các toán tử và ký hiệu dấu ngoặc đơn mở ‘(‘. Biểu thức hậu tố không chứa dấu ngoặc đơn. Chúng ta sẽ không xuất dấu ngoặc đơn trong đầu ra hậu tố.

Algorithm

1. Tạo một Stack
2. Với mỗi kí tự t trong luồng input
    if(t là 1 toán hạng) output t
    else if(t là một dấu ngoặc đơn phải ')' )
                Pop và output ra cho tới khi gặp dấu ngoặc đơn trái '(' (Nhưng không output) 
    else // t là một toán hạng hoặc một dấu ngoặc đơn trái
                Pop và output ra cho đến khi gặp phải một mức độ ưu tiên thấp hơn t hoặc dấu ngoặc đơn bên trái được b hoặc ngăn xếp trống.
                Push t
3. Pop và output ra cho tới khi Stack trống.

Để hiểu rõ hơn, chúng ta hãy theo dõi từng bước chuyển đổi của một ví dụ: A * B- (C + D) + E

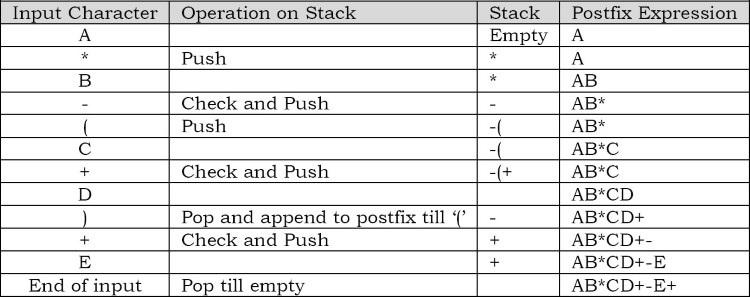
Problem-3

Đối với một mảng đã cho có n ký hiệu thì có bao nhiêu hoán vị ngăn xếp?

Solution: Số hoán vị ngăn xếp với n ký hiệu được biểu diễn bằng số Catalan và mình sẽ trình bày điều này trong chương Dynamic Programming.

Problem-4

Thảo luận về cách tính toán một biểu thức postfix sử dụng Stack?

Solution:
Algorithm:

1. Quét chuỗi Postfix từ trái sang phải.
2. Khởi tạo một ngăn xếp trống.
3. Lặp lại các bước 4 và 5 cho đến khi tất cả các ký tự được quét.
4. Nếu ký tự được quét là một toán hạng, hãy đẩy nó vào ngăn xếp.
5. Nếu ký tự được quét là một toán tử và nếu toán tử là một toán tử unary, thì pop một phần tử từ ngăn xếp. Nếu toán tử là một toán tử binary, thì pop hai phần tử từ ngăn xếp. Sau khi xuất các phần tử, hãy áp dụng toán tử cho các phần tử được pop đó. Để kết quả của thao tác này được retVal vào ngăn xếp. (Bạn có thể tham khảo thêm về các loại toán tử ở đây)
6. Sau khi tất cả các ký tự được quét, chúng ta sẽ chỉ có một phần tử trong ngăn xếp.
7. Kết quả là trả về đầu của ngăn xếp.

Ví dụ: Hãy để chúng tôi xem thuật toán trên hoạt động như thế nào bằng cách sử dụng một ví dụ. Giả sử rằng chuỗi postfix là 123 * + 5-. Ban đầu ngăn xếp trống. Bây giờ, ba ký tự đầu tiên được quét là 1, 2 và 3, là các toán hạng. Chúng sẽ được đẩy vào ngăn xếp theo thứ tự đó.

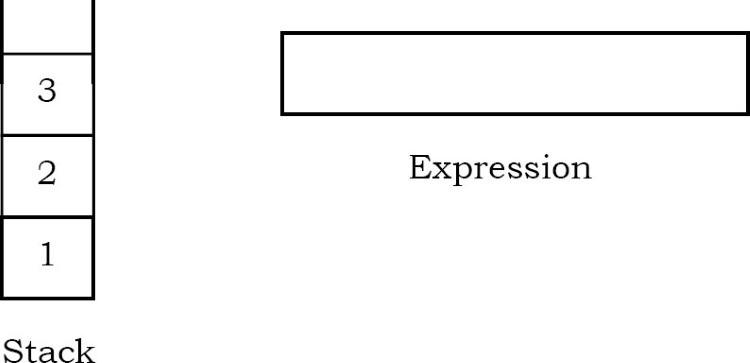
Ký tự tiếp theo được quét là “”, là một toán tử. Do đó, chúng tôi pop hai phần tử trên cùng khỏi ngăn xếp và thực hiện phép toán “” với hai toán hạng. Toán hạng thứ hai sẽ là phần tử đầu tiên được pop.

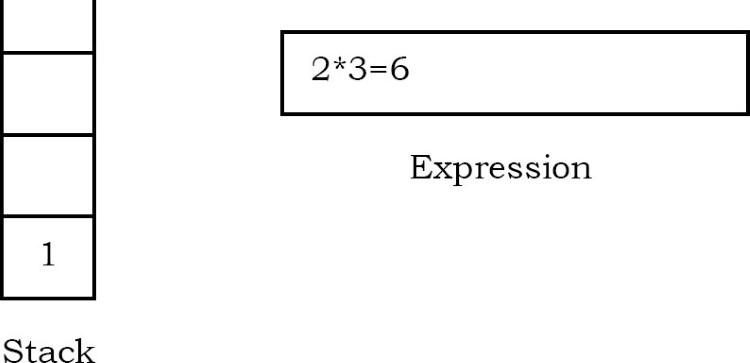
Giá trị của biểu thức (2 * 3) đã được tính bằng (6) được đẩy vào ngăn xếp.

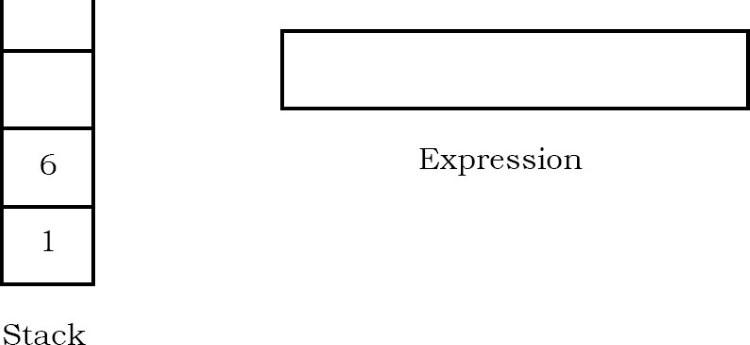
Ký tự tiếp theo được quét là “+”, là một toán tử. Do đó, chúng tôi pop hai phần tử trên cùng khỏi ngăn xếp và thực hiện phép toán “+” với hai toán hạng.
Toán hạng thứ hai sẽ là phần tử đầu tiên được xuất hiện.

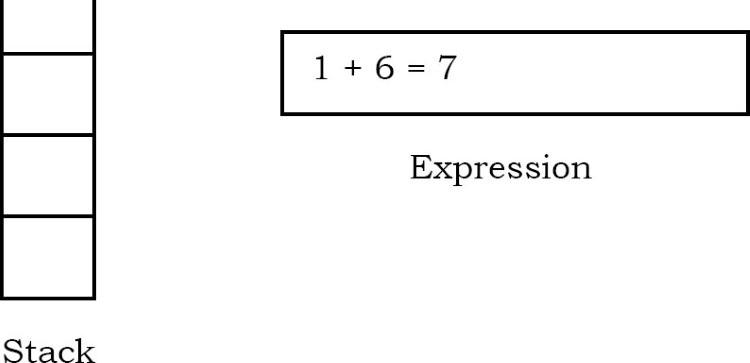
Giá trị của biểu thức (1 + 6) đã được tính bằng (7) được đẩy vào ngăn xếp.

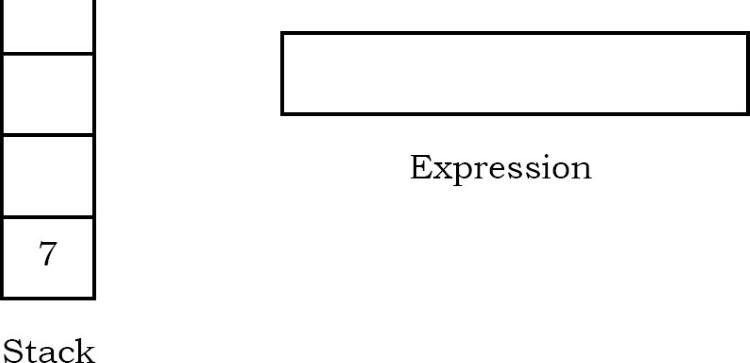
Ký tự tiếp theo được quét là “5”, được thêm vào ngăn xếp.

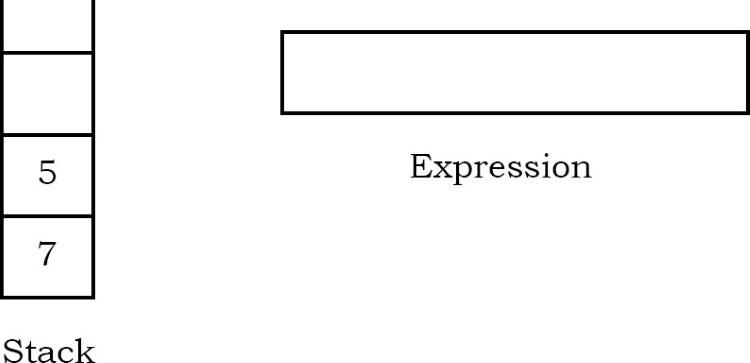
Ký tự tiếp theo được quét là “-”, là một toán tử. Do đó, chúng tôi pop hai phần tử trên cùng khỏi ngăn xếp và thực hiện phép toán “-” với hai toán hạng. Toán hạng thứ hai sẽ là phần tử đầu tiên được xuất hiện.

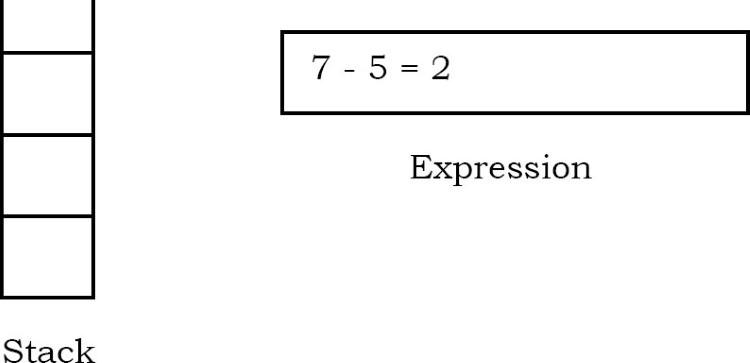
Giá trị của biểu thức (7-5) đã được tính bằng (2) được đẩy vào ngăn xếp.

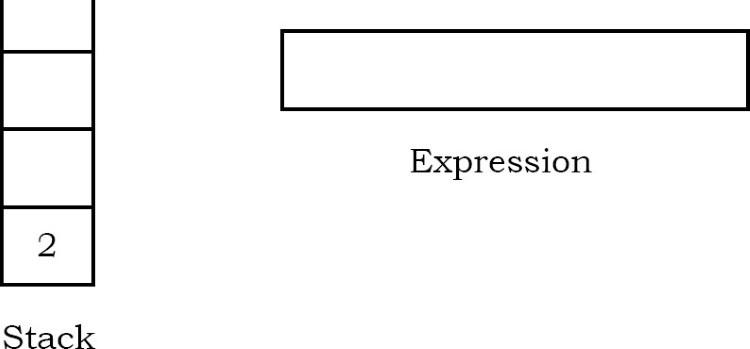
Bây giờ, vì tất cả các ký tự đã được quét, phần tử còn lại trong ngăn xếp (sẽ chỉ có một phần tử trong ngăn xếp) sẽ được trả về. Kết quả cuối cùng:

• Postfix String : 123*+5-
• Result : 2

	public int expressionEvaluation(String[] tokens) {
		Stack<Integer> s = new Stack<>();
		for (String token : tokens) {
			if (token.equals("+")) {
				int op1 = s.pop();
				int op2 = s.pop();
				int res = op1 + op2;
				s.push(res);
			} else if (token.equals("-")) {
				int op1 = s.pop();
				int op2 = s.pop();
				int res = op1 - op2;
				s.push(res);
			} else if (token.equals("*")) {
				int op1 = s.pop();
				int op2 = s.pop();
				int res = op1 * op2;
				s.push(res);
			} else if (token.equals("/")) {
				int op1 = s.pop();
				int op2 = s.pop();
				int res = op1 / op2;
				s.push(res);
			} else {
				s.push(Integer.parseInt(token));
			}
		}
		return s.pop();
	}

Problem-5

Chúng ta có thể đánh giá biểu thức infix với các ngăn xếp trong một lần quét không?

Solution: Sử dụng 2 ngăn xếp, chúng ta có thể đánh giá một biểu thức infix trong 1 lần vượt qua mà không cần chuyển đổi thành hậu tố.

Algorithm: Trong sách tác giả viết hơi khó hiểu, hoặc có thể in bị thiếu, ở bước 3 c => i.

Nên mình có tham khảo thêm ở đây:

1. Tạo hai ngăn xếp - ngăn xếp toán hạng và ngăn xếp toán tử.
2. Nếu phần tử được quét là toán hạng, đẩy vào ngăn xếp toán hạng.
3. Nếu là toán tử, hãy kiểm tra xem ngăn xếp toán tử có trống không.
4. Nếu ngăn xếp toán tử trống, hãy đẩy nó vào ngăn xếp toán tử.
5. Nếu ngăn xếp toán tử không trống, hãy so sánh mức độ ưu tiên của toán tử và ký tự trên cùng trong ngăn xếp. Nếu mức độ ưu tiên của ký tự lớn hơn hoặc bằng mức độ ưu tiên của đỉnh ngăn xếp của ngăn xếp toán tử, thì hãy đẩy ký tự vào ngăn xếp toán tử. Nếu không, hãy bật các phần tử khỏi ngăn xếp cho đến khi mức độ ưu tiên của ký tự ít hơn hoặc ngăn xếp trống.
6. Nếu ký tự là “(“, hãy đẩy nó vào ngăn xếp toán tử.
7. Nếu ký tự là “)”, hãy pop cho đến khi gặp “(” trong ngăn xếp toán tử.

Problem-6

Làm thế nào để thiết kế một ngăn xếp sao cho getMinimum() phải là $O (1)$?

Solution: Lấy một ngăn xếp bổ trợ duy trì mức tối thiểu của tất cả các giá trị trong ngăn xếp. Ngoài ra, giả sử rằng mỗi phần tử của ngăn xếp nhỏ hơn các phần tử bên dưới của nó. Để đơn giản, chúng ta hãy gọi là ngăn xếp phụ tối thiểu ngăn xếp. Khi chúng ta pop ngăn xếp chính, cũng pop ngăn xếp tối thiểu. Khi chúng tôi push ngăn xếp chính, hãy push phần tử mới hoặc mức tối thiểu hiện tại, tùy theo giá trị nào thấp hơn. Tại bất kỳ thời điểm nào, nếu chúng ta muốn nhận giá trị nhỏ nhất, thì chúng ta chỉ cần trả về phần tử trên cùng từ ngăn xếp min. Hãy để chúng tôi lấy một ví dụ và tìm ra nó. Ban đầu, chúng ta hãy giả sử rằng chúng ta đã đẩy 2, 6, 4, 1 và 5. Dựa trên thuật toán nói trên, ngăn xếp tối thiểu sẽ giống như sau:

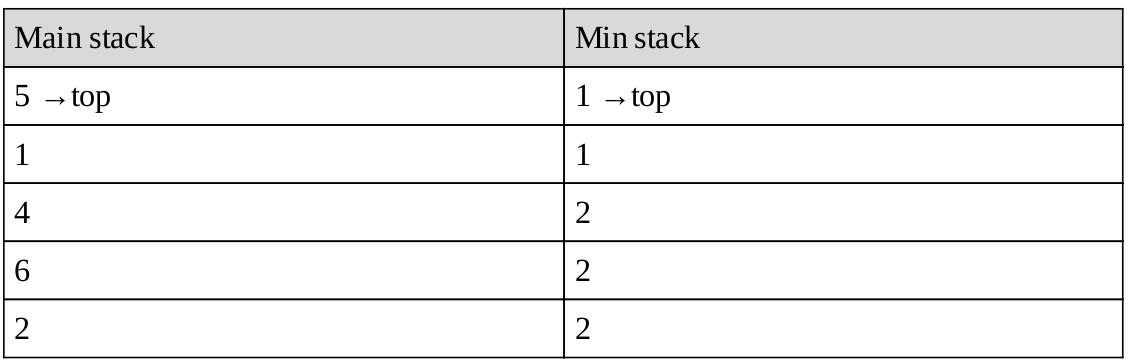
Sau khi pop hai lần, chúng tôi nhận được:

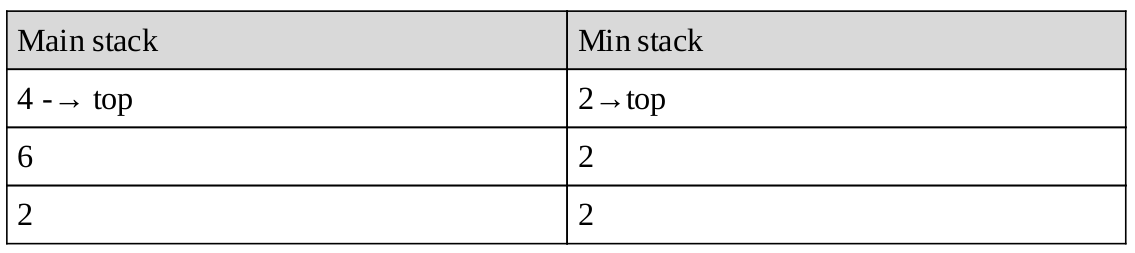
Dựa trên thảo luận ở trên, bây giờ chúng ta hãy viết mã các hoạt động push, pop và GetMinimum().

public class AdvancedStack{
	private Stack<Integer> elementStack = new Stack<>();
	private Stack<Integer>  minStack = new Stack<>();
	public void push(int data) {
		elementStack.push(data);
		if(minStack.isEmpty() || minStack.peek() >= data) {
			minStack.push(data);
		} else {
			minStack.push(minStack.peek());
		}
	}
	
	public Integer pop() {
		if(elementStack.isEmpty()) return null;
		minStack.pop();
		return elementStack.pop();
	}
	
	public int getMinimum() {
		return minStack.peek();
	}
	
	public boolean isEmpty() {
		return elementStack.isEmpty();
	}
}

Time complexity: O(1). Space complexity: O(n) [for Min stack].\

Problem-7

Đối với Problem-6, liệu có thể cải thiện độ phức tạp của không gian không?

Solution: Yes. Vấn đề chính của cách tiếp cận trước là, đối với mỗi thao tác đẩy, chúng tôi cũng đẩy phần tử trên lên ngăn xếp tối thiểu (hoặc phần tử mới hoặc phần tử tối thiểu hiện có). Điều đó có nghĩa là, chúng tôi đang đẩy các phần tử tối thiểu trùng lặp vào ngăn xếp.
Bây giờ, chúng ta hãy thay đổi thuật toán để cải thiện độ phức tạp của không gian. Chúng tôi vẫn có ngăn xếp tối thiểu, nhưng chúng ta chỉ pop ra khỏi nó khi giá trị chúng tôi bật ra từ ngăn xếp chính bằng với giá trị trên ngăn xếp tối thiểu. Chúng tôi chỉ đẩy lên ngăn xếp min khi giá trị được đẩy lên ngăn xếp chính nhỏ hơn hoặc bằng giá trị min hiện tại. Trong thuật toán đã sửa đổi này cũng vậy, nếu chúng ta muốn có giá trị nhỏ nhất thì chúng ta chỉ cần trả về phần tử trên cùng từ ngăn xếp min. Ví dụ: lấy phiên bản gốc và đẩy lại 1 lần nữa, chúng tôi sẽ nhận được:

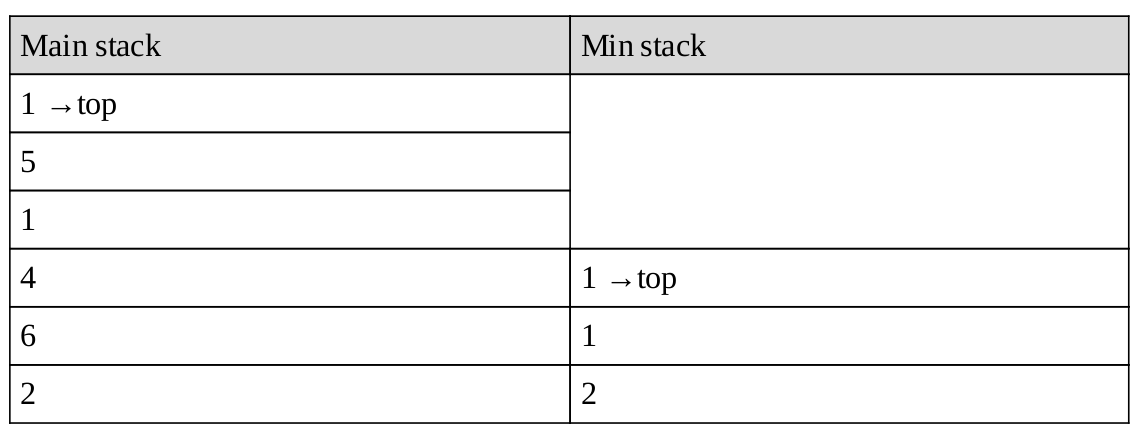
Pop từ cả 2 ngăn xếp vì 1==1, để lại:

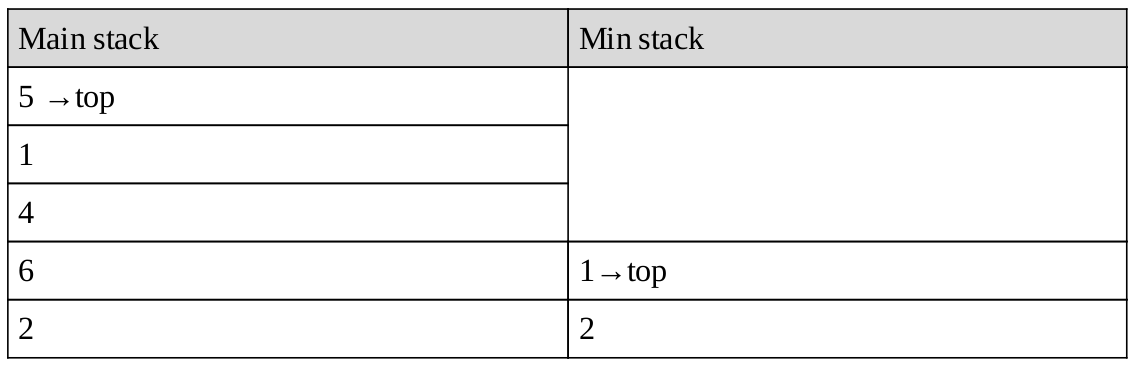
Tiếp theo chỉ pop từ main stack, vì 5 > 1:

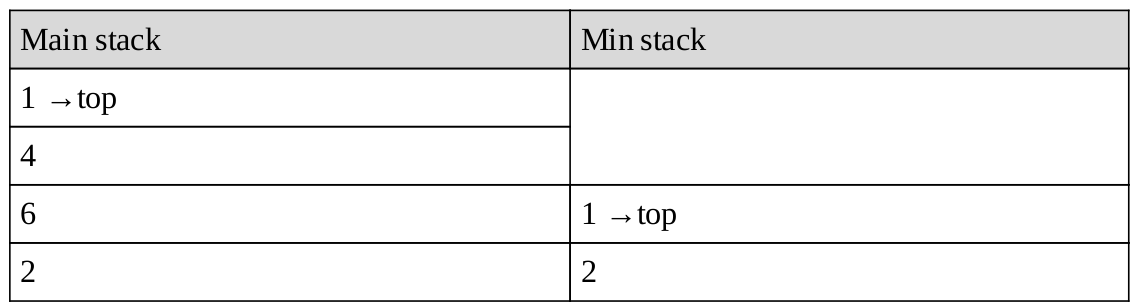
Lần tiếp theo sẽ pop cả 2 stacks vì 1 == 1:

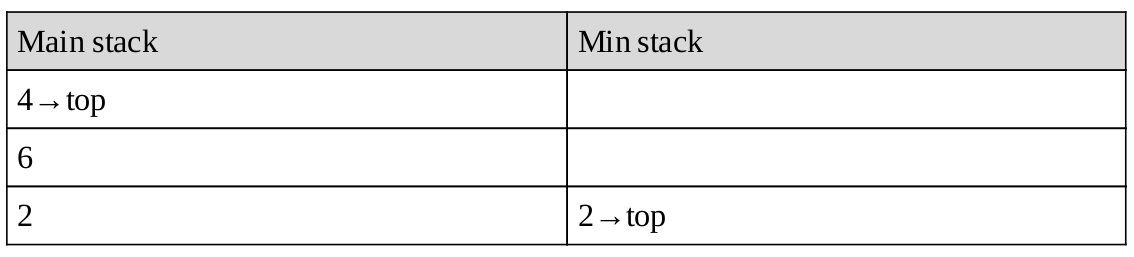
Lưu ý: Sự khác biệt chỉ là trong hoạt động push và pop.

public class AdvancedStack{
	private Stack<Integer> elementStack = new Stack<>();
	private Stack<Integer>  minStack = new Stack<>();
	public void push(int data) {
		elementStack.push(data);
		if(minStack.isEmpty() || minStack.peek() >= data) {
			minStack.push(data);
		} 
	}
	
	public Integer pop() {
		if(elementStack.isEmpty()) return null;
		
		Integer minTop = minStack.peek();
		Integer elementTop = elementStack.peek();
		if(minTop.intValue() == elementTop.intValue())
			minStack.pop();
		
		return elementStack.pop();
	}
	
	public int getMinimum() {
		return minStack.peek();
	}
	
	public boolean isEmpty() {
		return elementStack.isEmpty();
	}
}

Problem-8

Cho một mảng các ký tự được tạo thành với các kí tự a và b. Chuỗi được đánh dấu bằng ký tự đặc biệt X đại diện cho giữa danh sách (ví dụ: ababa… ababXbabab… ..baaa). Kiểm tra xem chuỗi có phải là palindrome hay không.

Solution: Đây là một trong những thuật toán đơn giản nhất. Những gì chúng ta làm là, bắt đầu hai chỉ mục, một ở đầu chuỗi và một ở cuối chuỗi. Mỗi lần so sánh xem các giá trị ở cả hai chỉ mục có giống nhau hay không. Nếu các giá trị không giống nhau thì chúng ta nói rằng chuỗi đã cho không phải là palindrome, nếu các giá trị giống nhau thì tăng chỉ số bên trái và giảm chỉ số bên phải. Tiếp tục quá trình này cho đến khi cả hai chỉ mục gặp nhau ở giữa (tại X) hoặc nếu chuỗi không phải là palindrome.

	public int isPalindrome(String inputStr) {
		int i = 0, j = inputStr.length();
		while(i < j && A[i] == A[j]) {
			i++;
			j--;
		}
		if(i<j) {
			System.out.println("Not a Palindrome");
			return 0;
		}else {
			System.out.println("Palindrome");
			return 1;
		}
	}

Time Complexity: O(n). Space Complexity: O(1).

Problem-9

Đối với Problem-8, nếu đầu vào nằm trong danh sách được liên kết đơn thì làm cách nào để kiểm tra xem các phần tử trong danh sách có tạo thành palindrome hay không (Điều đó có nghĩa là không thể di chuyển lùi lại).

Solution: Tham khảo Problem 39, mình đã có trình bày về vấn đề này

Problem-10

Chúng ta có thể giải quyết Problem-8 bằng cách sử dụng ngăn xếp không?

Solution: Yes
Algorithm

• Duyệt qua danh sách cho đến khi chúng ta gặp X là phần tử đầu vào.
• Trong quá trình truyền tải, đẩy tất cả các phần tử (cho đến X) vào ngăn xếp.
• Đối với nửa sau của danh sách, hãy so sánh nội dung của từng phần tử với phần trên cùng của ngăn xếp. Nếu chúng giống nhau thì hãy pop ngăn xếp và chuyển đến phần tử tiếp theo trong danh sách đầu vào.
• Nếu chúng không giống nhau thì chuỗi đã cho không phải là palindrome.
• Tiếp tục quá trình này cho đến khi ngăn xếp trống hoặc chuỗi không phải là palindrome.

	public boolean isPalindrome(String inputStr) {
		char inputChar[] = inputStr.toCharArray();
		Stack<Character> s = new Stack<>();
		int i = 0;
		while(inputChar[i] != 'X') {
			s.push(inputChar[i]);
			i++;
		}
		i++;
		while(i < inputChar.length) {
			if(s.isEmpty()) return false;
			if(inputChar[i] != s.pop().charValue()) {
				return false;
			}
			i++;
		}
		return true;
	}

Problem-11

Cho một ngăn xếp, làm thế nào để đảo ngược nội dung của ngăn xếp chỉ sử dụng các thao tác ngăn xếp (push và pop)?

Solution: Sử dụng đệ quy
Algorithm

• Đầu tiên pop tất cả các phần tử của ngăn xếp cho đến khi nó trở nên trống.
• Đối với mỗi bước quay lại trong đệ quy, hãy chèn phần tử vào cuối ngăn xếp.

	public static void reverseStack(Stack<Integer> stack) {
		if(stack.isEmpty()) return;
		int temp = stack.pop();
		reverseStack(stack);
		insertAtBottom(stack, temp);
	}
	
	public static void insertAtBottom(Stack<Integer> stack, int data) {
		if(stack.isEmpty()) {
			stack.push(data);
			return;
		}
		int temp = stack.pop();
		insertAtBottom(stack, data);
		stack.push(temp);
	}

Time Complexity: O(n2). Space Complexity: O(n), for recursive stack.

Problem-12

Chỉ ra cách triển khai một queue một cách hiệu quả bằng cách sử dụng hai stack. Phân tích thời gian chạy của các hoạt động hàng đợi.

Solution: Mình sẽ trình bày trong chương queue

Problem-13

Chỉ ra cách triển khai một stack một cách hiệu quả bằng cách sử dụng hai queue. Phân tích thời gian chạy của các hoạt động hàng đợi.

Solution: Mình sẽ trình bày trong chương queue

Problem-14

Làm cách nào để triển khai hai stack chỉ sử dụng một array? Các quy trình ngăn xếp của chúng ta không nên chỉ ra một ngoại lệ trừ khi mọi vị trí trong mảng được sử dụng?

Solution:

• Bắt đầu hai chỉ mục một ở đầu bên trái và chỉ mục kia ở đầu bên phải.
• Chỉ mục bên trái mô phỏng ngăn xếp đầu tiên và chỉ mục bên phải mô phỏng ngăn xếp thứ hai.
• Nếu chúng ta muốn đẩy một phần tử vào ngăn xếp đầu tiên thì hãy đặt phần tử đó ở chỉ mục bên trái.
• Tương tự, nếu chúng ta muốn đẩy một phần tử vào ngăn xếp thứ hai thì hãy đặt phần tử tại chỉ số bên phải.
• Ngăn xếp đầu tiên phát triển về phía bên phải và ngăn xếp thứ hai phát triển về phía bên trái.

public class ArrayWithTwoStack{
	private Integer[] dataArray;
	private int size, topOne, topTwo;
	public ArrayWithTwoStack(int size) {
		if(size < 2) throw new IllegalStateException("size < 2 is no persmissible");
		dataArray = new Integer[size];
		this.size = size;
		topOne = -1;
		topTwo = size;
	}
	
	public void push(int stackId, int data) {
		if(topTwo == topOne+1) throw new StackOverflowError("Array is full");
		if(stackId == 1) {
			dataArray[++topOne] = data;
		}else if(stackId == 2) {
			dataArray[--topTwo] = data;
		}else return;
	}
	
	public Integer pop(int stackId) {
		if(stackId == 1) {
			if(topOne == 1) throw new EmptyStackException();
			int toPop = dataArray[topOne];
			dataArray[topOne--] = null;
			return toPop;
		}else if(stackId == 2) {
			if(topTwo == this.size) throw new EmptyStackException();
			int toPop = dataArray[topTwo];
			dataArray[topTwo++] = null;
			return toPop;
		} else return null;
	}
	
	public boolean isEmpty(int stackId) {
		if(stackId == 1) {
			return topOne == -1;
		} else if(stackId == 2) {
			return topTwo == this.size;
		} else return true;
	}
}