Chương 6: TREES - 4.Lý thuyết và bài tập về Generic Trees

6.5 Generic Trees (N-ary Trees)

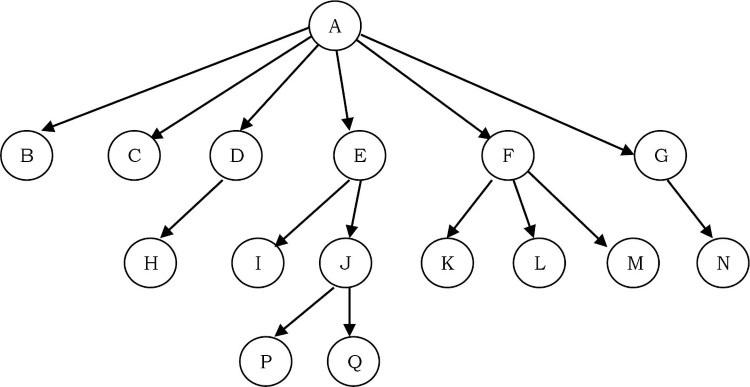
Trong phần trước chúng ta đã thảo luận về cây nhị phân trong đó mỗi nút có thể có tối đa hai nút con và chúng được biểu diễn dễ dàng bằng hai pointers. Nhưng giả sử nếu chúng ta có một cây với nhiều nút con ở mỗi nút và nếu chúng ta không biết một nút có thể có bao nhiêu nút con, thì chúng ta biểu diễn chúng như thế nào?
Ví dụ, hãy xem xét cái cây được hiển thị ở trên.

Làm thế nào để chúng ta biểu diễn cho cây?

Trong cây trên, có các nút có 6 node con, có 3 node con, có 2 node con, có 1 node con và không có node con (node lá). Để trình bày cây này, chúng ta phải xem xét trường hợp xấu nhất (6 node con) và phân bổ nhiều con trỏ con đó cho mỗi nút. Dựa trên điều này, biểu diễn nút có thể được đưa ra là:

Vì chúng tôi không sử dụng tất cả các con trỏ trong tất cả các trường hợp, nên rất lãng phí bộ nhớ. Một vấn đề khác là chúng ta không biết trước số nút con cho mỗi node. Để giải quyết vấn đề này, chúng ta cần một biểu diễn giảm thiểu sự lãng phí và cũng chấp nhận các node có số node con bất kỳ.

Biểu diễn của Generic Trees

Vì mục tiêu của chúng tôi là tiếp cận tất cả các node của cây, nên một giải pháp khả thi cho vấn đề này là như sau:

• Tại mỗi node liên kết node con của cùng node cha (sibling - node anh em) từ trái sang phải.
• Xóa các liên kết từ node cha đến tất cả node con ngoại trừ node con đầu tiên.

Những điều trên nói rằng nếu chúng ta có một liên kết giữa các node con thì chúng ta không cần thêm các liên kết từ node cha đến tất cả các node con. Điều này là do chúng ta có thể duyệt qua tất cả các phần tử bằng cách bắt đầu từ phần tử con đầu tiên của phần tử cha. Vì vậy, nếu chúng tôi có một liên kết giữa node cha mẹ và node con đầu tiên và cũng có liên kết giữa tất cả các node con của cùng một node cha thì nó sẽ giải quyết được vấn đề của chúng ta.

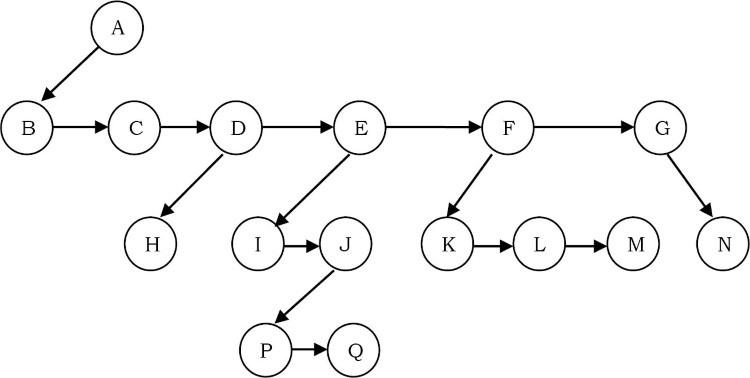
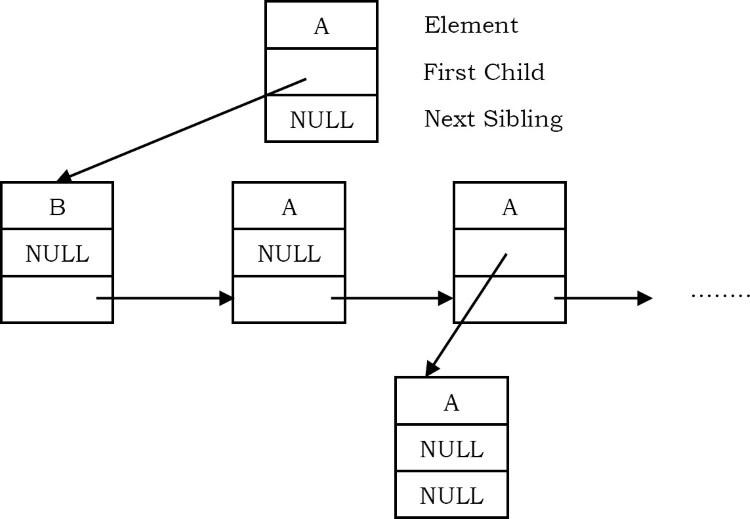
Biểu diễn này đôi khi được gọi là biểu diễn first child/next sibling( node con đầu tiên/ node anh em tiếp theo). Biểu diễn này được hiển thị ở trên. Thực tế trong hệ thống cho cây này là:

Dựa trên những gì đã trình bày ở trên, khai báo cây tổng quát có thể được đưa ra như sau:

public class TreeNode {
    public int data;
    public TreeNode firstChild;
    public TreeNode nextSibling;

    public int getData() {
        return data;
    }

    public void setData(int data) {
        this.data = data;
    }

    public TreeNode getFirstChild() {
        return firstChild;
    }

    public void setFirstChild(TreeNode firstChild) {
        this.firstChild = firstChild;
    }

    public TreeNode getNextSibling() {
        return nextSibling;
    }

    public void setNextSibling(TreeNode nextSibling) {
        this.nextSibling = nextSibling;
    }
}

Lưu ý: Vì chúng ta có thể chuyển đổi bất kỳ generic tree nào thành biểu diễn nhị phân, nên trong thực tế, chúng tôi sử dụng cây nhị phân. Chúng ta có thể coi tất cả các generic tree với biểu diễn first child/next sibling là cây nhị phân.

Generic Trees: Problems & Solutions

Problem-41

Cho một cái cây, hãy đưa ra thuật toán tìm tổng tất cả các phần tử của cây.

Solution: Giải pháp tương tự như những gì chúng ta đã làm đối với cây nhị phân. Điều đó có nghĩa là duyệt qua toàn bộ cây và tiếp tục thêm các giá trị. Chúng ta có thể sử dụng level order traversal hoặc đệ quy.

	public int findSum(BinaryTreeNode root){
		if(root == null){
			return 0;
		}
		return root.getData() + findSum(root.getLeft()) + findSum(root.getRight());
	}

Lưu ý: Tất cả các vấn đề mà chúng ta đã thảo luận về cây nhị phân cũng có thể áp dụng cho cây tổng quát. Thay vì con trỏ trái và phải, chúng ta chỉ cần sử dụng firstChild và nextSibling.

Problem-42

Đối với cây 4-ary (mỗi nút có thể chứa tối đa 4 nút con), chiều cao tối đa có thể có với 100 nút là bao nhiêu? Giả sử chiều cao của một single node là 0.

Solution: Trong cây 4-ary, mỗi nút có thể chứa từ 0 đến 4 nút con và để đạt được chiều cao tối đa, chúng ta chỉ cần giữ một nút con cho mỗi nút cha. Với 100 nút, chiều cao tối đa có thể có là 99. Nếu chúng ta có một hạn chế là ít nhất một nút có 4 nút con, thì chúng ta giữ một nút có 4 nút con và các nút còn lại có 1 nút con. Trong trường hợp này, chiều cao tối đa có thể là 96. Tương tự, với n nút, chiều cao tối đa có thể là n – 4.

Problem-43

Đối với cây 4-ary (mỗi nút có thể chứa tối đa 4 nút con), chiều cao tối thiểu có thể có với n nút là bao nhiêu?

Solution: Tương tự như thảo luận ở trên, nếu chúng ta muốn có chiều cao tối thiểu, thì chúng ta cần lấp đầy tất cả các nút bằng các nút con tối đa (trong trường hợp này là 4). Bây giờ hãy xem bảng sau, cho biết số nút tối đa cho một độ cao nhất định.

Đối với một độ cao h nhất định, các nút tối đa có thể là: $\frac { 4 ^ { h + 1 } - 1 } { 3 }$. Để có được chiều cao tối thiểu, lấy logarit ở cả hai phía:

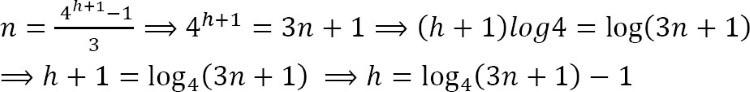
Problem-44

Cho một mảng P, trong đó P[i] chỉ cha của nút thứ i trong cây (giả sử nút gốc được biểu thị bằng –1). Đưa ra thuật toán tìm chiều cao hoặc độ sâu của cây.

Solution: Từ định nghĩa vấn đề, mảng đã cho đại diện cho cây. Điều đó có nghĩa là, chúng ta cần xem xét cây cho mảng đó và tìm độ sâu của cây.

Ví dụ: nếu P là

Cây tương ứng của nó là:

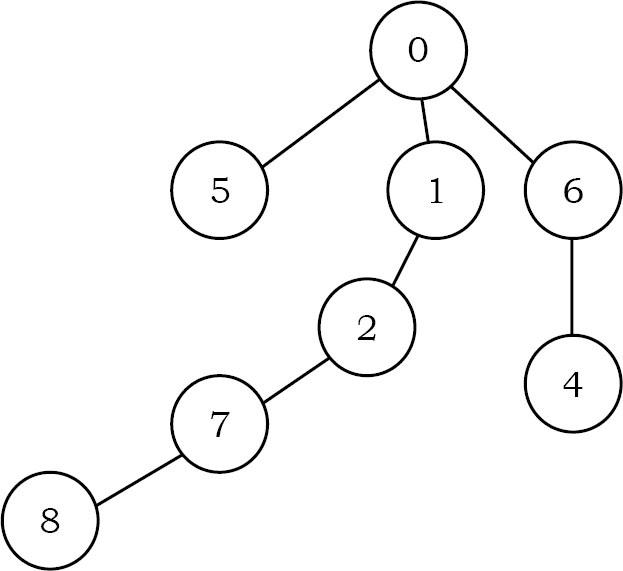
Độ sâu của cây đã cho này là 4. Nếu cẩn thận quan sát, chúng ta chỉ cần bắt đầu từ mọi nút và tiếp tục đi đến cha của nó cho đến khi đạt đến –1 và cũng theo dõi độ sâu tối đa giữa tất cả các nút.

	public int findDepthInGenericTree(int[] P){
		int maxDepth = -1, currentDepth = -1, j;
		for(int i = 0; i < P.length; i++){
			currentDepth = 0;
			j = i;
			while(P[j] != -1){
				currentDepth++;
				j = P[j];
			}
			if(currentDepth > maxDepth){
				maxDepth = currentDepth;
			}
		}
		return maxDepth;
	}

Time Complexity: $O(n^2$). Đối với cây nghiêng(skew trees - các node lệch về một phía), chúng ta sẽ tính đi tính lại các giá trị giống nhau.
Space Complexity: $O(1)$.

Lưu ý: Chúng tôi có thể tối ưu hóa mã bằng cách lưu trữ độ sâu của các nút được tính toán trước đó trong một số bảng băm hoặc mảng khác. Điều này làm giảm độ phức tạp về thời gian nhưng sử dụng thêm không gian.

Problem-45

Cho một node trong generic tree, hãy tìm số node anh em của node đó.

Solution: Đối với một nút nhất định trong cây, chúng ta chỉ cần duyệt qua tất cả các node next siblings của nó.

	public int siblingsCount(TreeNode current){
		int count = 0;
		while(current != null){
			count++;
			current = current.getNextSibling();
		}
		return count;
	}

Time Complexity: O(n). Space Complexity: O(1).

Problem-46

Cho hai cây, làm cách nào để kiểm tra xem các cây đó có đồng dạng với nhau hay không?

Solution: Hai cây nhị phân root1 và root2 là đồng dạng nếu chúng có cùng cấu trúc. Giá trị của các node không ảnh hưởng đến việc hai cây có đồng dạng hay không. Trong sơ đồ bên dưới, cây ở giữa không đồng dạng với các cây khác, nhưng cây bên phải đồng dạng với cây bên trái.

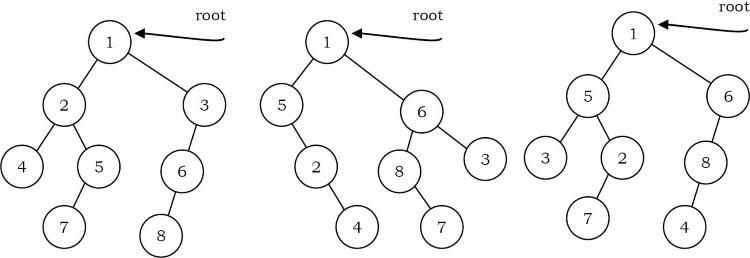
	public int isIsomorphic(TreeNode root1, TreeNode root2){
		if(root1 == null && root2 == null){
			return 1;
		}
		if((root1 == null && root2 != null) || (root1 != null && root2 == null)){
			return 0;
		}
		return (isIsomorphic(root1.getFirstChild(), root2.getFirstChild()) & isIsomorphic(root1.getNextSibling(), root2.getNextSibling());
	}

Problem-47

Cho hai cây, làm cách nào để kiểm tra xem chúng có gần như đồng dạng(quasi-isomorphic) với nhau hay không?

Solution: Hai cây root1 và root2 quasi-isomorphic nếu root1 có thể được chuyển đổi thành root2 bằng cách hoán đổi con trái và con phải của một số nút của root1. Dữ liệu trong các nút không quan trọng trong việc xác định quasi-isomorphic; chỉ có hình dạng là quan trọng. Các cây bên dưới quasi-isomorphic vì nếu hoán đổi các nút con của các nút bên trái thì sẽ thu được cây bên phải.

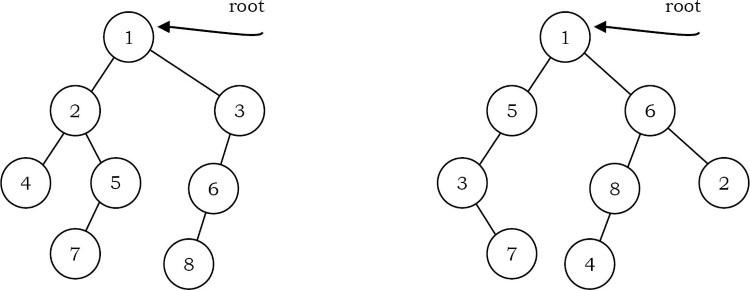
	public boolean isQuasilIsomorphic(TreeNode root1, TreeNode root2){
		if(root1 == null && root2 == null){
			return true;
		}
		if(((root1==null) && (root2 != null)) || (root1 != null && root2 == null)){
			return false;
		}
		return (isQuasilIsomorphic(root1.getFirstChild(), root2.getFirstChild()) && isQuasilIsomorphic(root1.getNextSibling(), root2.getNextSibling()))
				|| (isQuasilIsomorphic(root1.getFirstChild(), root2.getNextSibling()) && isQuasilIsomorphic(root1.getNextSibling(), root2.getFirstChild()));
	}

Problem-48

Cho một nút trong cây tổng quát, hãy đưa ra thuật toán đếm số nút con của nút đó.

Solution: Đối với một nút nhất định trong cây, chúng ta chỉ cần trỏ tới nút con đầu tiên của nó và tiếp tục duyệt qua tất cả các nút anh chị em tiếp theo của nó.

	public int childCount(TreeNode current){
		int count = 0;
		current = current.getFirstChild();
		while(current != null){
			count++;
			current = current.getNextSibling();
		}
		return count;
	}

Time Complexity: O(n). Space Complexity: O(1).

Problem-49

Cây k-ary đầy đủ là cây mà mỗi nút có 0 hoặc k node con. Cho một mảng chứa preorder traversal của cây k -ary đầy đủ, hãy đưa ra thuật toán để xây dựng cây k -ary đầy đủ.

Solution:

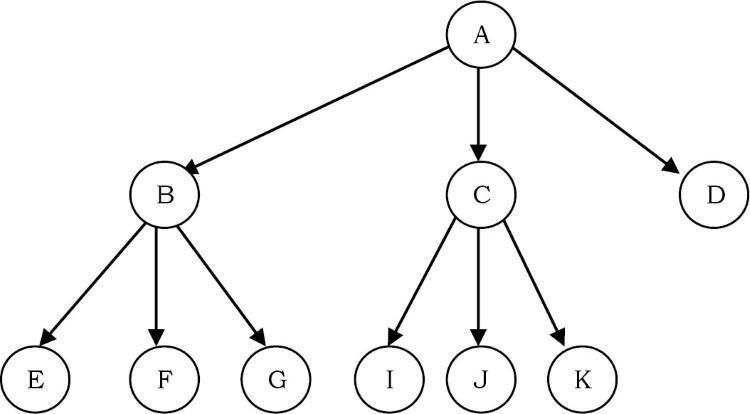
Như chúng ta đã thấy, trong quá trình duyệt preorder traversal, nút gốc đầu tiên được xử lý, sau đó là cây con bên trái và cây con bên phải. Do đó, để xây dựng một k-ary đầy đủ, chúng ta chỉ cần tiếp tục tạo các nút mà không cần quan tâm đến các nút đã xây dựng trước đó. Chúng ta có thể sử dụng thủ thuật này để xây dựng cây một cách đệ quy bằng cách sử dụng một global index. Khai báo cho cây k-ary có thể được đưa ra như sau:

// Java program to construct a binary tree from preorder traversal
  
// A Binary Tree node
class Node
{
    int data;
    Node left, right;
  
    Node(int item)
    {
        data = item;
        left = right = null;
    }
}
  
class Index
{
    int index = 0;
}
  
class BinaryTree
{
    Node root;
    Index myindex = new Index();
  
    /* A recursive function to create a Binary Tree from given pre[]
       preLN[] arrays. The function returns root of tree. index_ptr is used
       to update index values in recursive calls. index must be initially
       passed as 0 */
    Node constructTreeUtil(int pre[], char preLN[], Index index_ptr,
                                                     int n, Node temp)
    {
        // store the current value of index in pre[]
        int index = index_ptr.index;
  
        // Base Case: All nodes are constructed
        if (index == n)
            return null;
  
        // Allocate memory for this node and increment index for
        // subsequent recursive calls
        temp = new Node(pre[index]);
        (index_ptr.index)++;
  
        // If this is an internal node, construct left and right subtrees
        // and link the subtrees
        if (preLN[index] == 'N')
        {
            temp.left = constructTreeUtil(pre, preLN, index_ptr, n,
                                                               temp.left);
            temp.right = constructTreeUtil(pre, preLN, index_ptr, n,
                                                               temp.right);
        }
  
        return temp;
    }
  
    // A wrapper over constructTreeUtil()
    Node constructTree(int pre[], char preLN[], int n, Node node)
    {
        // Initialize index as 0. Value of index is used in recursion to
        // maintain the current index in pre[] and preLN[] arrays.
        int index = 0;
  
        return constructTreeUtil(pre, preLN, myindex, n, node);
    }
  
    /* This function is used only for testing */
    void printInorder(Node node)
    {
        if (node == null)
            return;
  
        /* first recur on left child */
        printInorder(node.left);
  
        /* then print the data of node */
        System.out.print(node.data + " ");
  
        /* now recur on right child */
        printInorder(node.right);
    }
  
    // driver function to test the above functions
    public static void main(String args[])
    {
        BinaryTree tree = new BinaryTree();
        int pre[] = new int[]{10, 30, 20, 5, 15};
        char preLN[] = new char[]{'N', 'N', 'L', 'L', 'L'};
        int n = pre.length;
  
        // construct the above tree
        Node mynode = tree.constructTree(pre, preLN, n, tree.root);
  
        // Test the constructed tree
        System.out.println("Following is Inorder Traversal of the" 
                                      + "Constructed Binary Tree: ");
        tree.printInorder(mynode);
    }
}

Bài này code mình có tham khảo ở đây
Độ phức tạp về thời gian: O(n), trong đó n là kích thước của mảng đã cho. Điều này là do chúng tôi đang di chuyển tuần tự và không truy cập vào các node đã được xây dựng.