Chương 1: Introduction - 3.Độ phức tạp thuật toán
Bài đăng này đã không được cập nhật trong 3 năm
Ở bài viết trước chúng ta đã có idea solution cho việc phân tích và so sánh các thuật toán: "Thể hiện thời gian chạy của một thuật toán nhất định dưới dạng một hàm của kích thước đầu vào n (tức là f (n)) và so sánh các hàm khác nhau này".
Để phân tích các hàm số này, chúng ta sẽ đi vào một số khái niệm về toán học và đồ thị.
Tất cả đều là các kiến thức chúng ta đã được học từ cấp 3 và cả đại học, hồi mình đọc cũng thấy mình đã quên gần hết 😅, nhưng không sao, chỉ cần gg search xem lại một chút là sẽ nhớ ngay 😁
1.8 What is Rate of Growth?
Nguyên văn khái niệm tiếng anh: The rate at which the running time increases as a function of input is called rate of growth.
Tốc độ mà thời gian chạy tăng lên như một hàm của đầu vào được gọi là Rate of Growth(tốc độ biến thiên).
Một khái niệm khá trừu tượng, để mình lấy ví dụ mọi người sẽ hiểu hơn:
- Hãy giả sử rằng bạn đến một cửa hàng để mua một chiếc ô tô và một chiếc xe đạp.
- Nếu bạn của bạn nhìn thấy bạn ở đó và hỏi bạn đang mua gì, thì nói chung bạn sẽ nói là mua một chiếc xe hơi.
- Điều này là do giá của chiếc xe hơi cao so rất nhiều với giá của xe đạp, khiến cho giá của chiếc xe đạp hầu như không còn đáng kể.
Total Cost = cost_of_car + cost_of_bicycle
Vì giá của chiếc ô tô là rất lớn so với xe đạp(ví dụ Mercedes AMG 13 tỉ, chiếc xe đạp mini Nhật bãi 300k)
=> Total Cost ≈ cost_of_car (xấp xỉ)
Đối với ví dụ được đề cập ở trên, chúng ta có thể biểu thị chi phí của ô tô và chi phí của xe đạp theo hàm, và đối với một hàm đã cho, hãy bỏ qua các bậc thấp tương đối không đáng kể (đối với giá trị lớn của kích thước đầu vào, n) .
Ví dụ, trong trường hợp dưới đây, n^4, 2 * n^2, 100n và 500 là chi phí riêng lẻ của một số hàm và gần đúng với n^4 vì n^4 là tốc độ biến thiên cao nhất.
n^4 + (2 * n^2) + 100n + 500 ≈ n^4
1.9 Commonly used Rates of Growth
Dưới đây là danh sách các tỷ lệ tăng trưởng mà bạn sẽ gặp trong các chương sau.
| Time Complexity | Name | Ví dụ |
|---|---|---|
| 1 | Constant | Thêm 1 phần từ vào đầu của 1 Linked List |
| logn | Logarithmic | Tìm 1 phần tử trong 1 array đã được sắp xếp |
| n | Linear | Tìm 1 phần tử trong 1 array chưa được sắp xếp |
| nlogn | Linear Logarithmic | Sorting n phần tử bằng thuật toán Mergesort |
| n^2 | Quadratic | Đường đi ngắn nhất giữa hai nút trong đồ thị |
| n^3 | Cubic | Phép nhân ma trận |
| 2^n | Exponential | Bài toán tháp Hà Nội |
Biểu đồ dưới đây cho thấy mối quan hệ giữa các tốc độ biến thiên khác nhau.
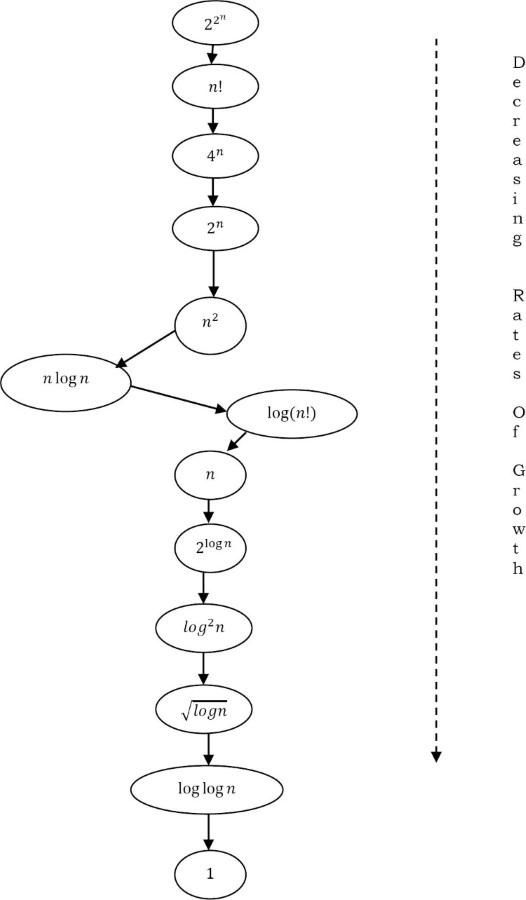
1.10 Types of Analysis
Để phân tích thuật toán đã cho, chúng ta cần biết loại input nào thì thuật toán mất ít thời gian hơn (performing well - hoạt động tốt) và loại input nào thì thuật toán mất nhiều thời gian hơn.
Yeah, chỗ này hơi khó hiểu một chút, cùng thuật toán mà lại phụ thuộc đầu vào input @@
Để mình ví dụ, cùng 1 thuật toán sắp xếp Insertion Sort mất thời gian tối đa(O(n^2)) để sắp xếp nếu các phần tử được sắp xếp theo thứ tự ngược lại. Và cần thời gian tối thiểu (O(n)) khi các phần tử đã được sắp xếp.(Khi nào tới chương về các thuật toán sắp xếp mình sẽ nói kĩ hơn).
Chúng ta cũng đã thấy rằng một thuật toán có thể được biểu diễn dưới dạng một biểu thức.
Điều đó có nghĩa là chúng ta biểu diễn thuật toán với nhiều biểu thức: một cho trường hợp cần ít thời gian hơn và một cho trường hợp cần nhiều thời gian hơn.(Chính là 2 case như trong ví dụ mình vừa lấy trên).
Nói chung, trường hợp đầu tiên được gọi là trường hợp xấu nhất và trường hợp thứ hai được gọi là trường hợp tốt cho thuật toán.
Để phân tích một thuật toán, chúng ta cần một số loại cú pháp và điều đó tạo thành cơ sở cho asymptotic analysis/notation(phân tích và ký hiệu tiệm cận).
Có ba loại phân tích:
- Worst case - Trường hợp tệ nhất có thể xảy ra
- Xác định input mà thuật toán mất nhiều thời gian (thời gian hoàn thành chậm nhất).
- Input là đầu vào mà thuật toán chạy chậm nhất.
- Best case - Trường hợp tốt nhất có thể xảy ra
- Xác định input mà thuật toán mất ít thời gian nhất (thời gian hoàn thành nhanh nhất).
- Input là đầu vào mà thuật toán chạy nhanh nhất.
- Average case - Trường hợp trung bình
- Cung cấp dự đoán về thời gian chạy của thuật toán.
- Chạy thuật toán nhiều lần, sử dụng nhiều input khác nhau đến từ nhiều nguồn khác nhau, tính tổng thời gian chạy (bằng cách cộng các thời gian riêng lẻ) và chia cho số lần thử.
- Giả sử rằng input là ngẫu nhiên.
Lower Bound <= Average Time < Upper Bound
Đối với một thuật toán nhất định, chúng ta có thể biểu diễn các trường hợp tốt nhất, xấu nhất và trung bình dưới dạng biểu thức. Ví dụ, cho f (n) là hàm, đại diện cho thuật toán đã cho.
f(n) = n^2 + 500 , for worst case
f(n) = n + 100n + 500, for best case
Tương tự như vậy đối với trường hợp trung bình.
Biểu thức xác định các input mà thuật toán lấy thời gian chạy trung bình (hoặc không gian bộ nhớ).
Tạm kết
Bài viết khá dài rồi, mình sẽ dừng ở đây, bài tiếp theo mình sẽ trình bày chi tiết về cách mà chúng ta sẽ biểu diễn 3 trường hợp xảy ra với 1 hàm toán học như đã trình bày ở trên sử dụng các kí hiệu và đồ thị để minh họa.
All rights reserved