Chương 10: SELECTION ALGORITHMS- 1.Lý thuyết cơ bản
Bài đăng này đã không được cập nhật trong 2 năm
12.1 Thuật toán Selection(lựa chọn) là gì?
Thuật toán Selection là thuật toán tìm số nhỏ nhất/lớn nhất thứ k trong một danh sách (còn gọi là order statistic - thống kê bậc k). Điều này bao gồm việc tìm kiếm các phần tử nhỏ nhất, lớn nhất và trung bình. Để tìm thống kê bậc k, có nhiều giải pháp có độ phức tạp khác nhau và trong chương này, chúng ta sẽ liệt kê các khả năng đó.
12.2 Selection bằng cách sắp xếp
Một vấn đề lựa chọn có thể được chuyển đổi thành một vấn đề sắp xếp. Trong phương pháp này, trước tiên chúng ta sắp xếp các phần tử đầu vào và sau đó lấy phần tử mong muốn. Sẽ hiệu quả nếu chúng ta muốn thực hiện nhiều lựa chọn.
Ví dụ: giả sử chúng ta muốn lấy phần tử tối thiểu. Sau khi sắp xếp các phần tử đầu vào, chúng ta chỉ cần trả về phần tử đầu tiên (giả sử mảng được sắp xếp theo thứ tự tăng dần). Bây giờ, nếu chúng ta muốn tìm phần tử nhỏ thứ hai, chúng ta chỉ cần trả về phần tử thứ hai từ danh sách đã sắp xếp.
Điều đó có nghĩa là, đối với phần tử nhỏ thứ hai, chúng tôi sẽ không thực hiện sắp xếp lại. Điều tương tự cũng xảy ra với các truy vấn tiếp theo. Ngay cả khi chúng ta muốn lấy phần tử nhỏ nhất thứ k, chỉ cần một lần quét danh sách đã sắp xếp là đủ để tìm phần tử (hoặc chúng ta có thể trả về giá trị được index thứ k nếu các phần tử nằm trong mảng).
Từ cuộc thảo luận ở trên, những gì chúng ta có thể nói là, với cách sắp xếp ban đầu, chúng ta có thể trả lời bất kỳ truy vấn nào trong một lần quét, O(n). Nói chung, phương pháp này yêu cầu thời gian O(nlogn) (để sắp xếp), trong đó n là độ dài của danh sách đầu vào. Giả sử chúng ta đang thực hiện n truy vấn, thì chi phí trung bình cho mỗi thao tác chỉ là . Loại phân tích này được gọi là phân tích khấu hao.
12.3 Thuật toán Selection dựa trên phân vùng
Đối với lựa chọn dựa trên phân vùng, một biến thể của thuật toán Quick sort được sử dụng. Chúng ta chọn một phần tử trục và sử dụng bước phân vùng từ thuật toán sắp xếp nhanh để sắp xếp tất cả các phần tử nhỏ hơn trục ở bên trái của nó và các phần tử lớn hơn ở bên phải của nó. Nhưng trong khi Quicksort lặp lại trên cả hai phía của phân vùng, thì biến thể này chỉ lặp lại trên một phía, phía có phần tử thứ k mong muốn. Các thuật toán dựa trên phân vùng được thực hiện tại chỗ, dẫn đến việc sắp xếp một phần dữ liệu. Chúng ta có thể được thực hiện ngoài vị trí bằng cách không thay đổi dữ liệu gốc với chi phí là không gian phụ trợ O(n).
12.4 Thuật toán Selection tuyến tính

Selection Algorithms: Problems & Solutions
Problem-1
Tìm phần tử lớn nhất trong mảng A kích thước n.
Solution: Quét toàn bộ mảng và trả về phần tử lớn nhất.
public void FindLargestInArray(int n, int[] A){
int large = A[0];
for (int i = 0; i < n - 1; i++) {
if(A[i] > large){
large = A[i];
}
}
System.out.println("Largest: " + large);
}
Time Complexity - O(n). Space Complexity - O(1).
Note: Bất kỳ thuật toán xác định nào có thể tìm thấy khóa lớn nhất trong số n khóa bằng cách so sánh các khóa đều cần ít nhất n -1 phép so sánh.
Problem-2
Tìm phần tử nhỏ nhất và lớn nhất trong mảng A kích thước n.
Solution:
public void FindSmallestAndLargestInArray(int n, int[] A){
int large = A[0];
int small = A[0];
for (int i = 0; i < n - 1; i++) {
if(A[i] < small){
small = A[i];
} else if (A[i] > large) {
large = A[i];
}
}
System.out.println("Largest: " + large);
System.out.println("smallest: " + small);
}
Time Complexity - O(n). Space Complexity - O(1). Số lần so sánh trong trường hợp xấu nhất là 2(n-1).
Problem-3
Chúng ta có thể cải thiện các thuật toán trên không?
Solution: Yes. Chúng ta có thể làm điều này bằng cách so sánh theo cặp.
public void FindWithPairComparison(int n, int[] A){
int large = -1;
int small = -1;
for (int i = 0; i < n - 1; i+=2) {
if(A[i] < A[i+1]){
if(A[i] < small){
small = A[i];
}
if (A[i+1] > large) {
large = A[i+1];
}
} else {
if(A[i+1] < small){
small = A[i+1];
}
if (A[i+1] > large) {
large = A[i+1];
}
}
}
System.out.println("Largest: " + large);
System.out.println("smallest: " + small);
}
Time Complexity - O(n). Space Complexity - O(1).
Số lần so sánh:
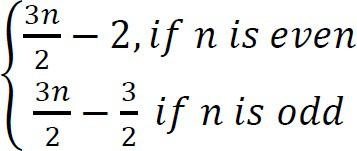
Problem-4
Đưa ra thuật toán tìm phần tử lớn thứ hai trong danh sách các phần tử đã cho.
Solution: Brute Force Method
Algorithm:
- Tìm phần tử lớn nhất: cần n – 1 phép so sánh
- Xóa (bỏ) phần tử lớn nhất
- Lại tìm phần tử lớn nhất: cần n – 2 phép so sánh
Tổng số lần so sánh:
Problem-5
Chúng ta có thể giảm số lần so sánh trong giải pháp của Problem-4 không?
Solution: Phương thức Tournament:
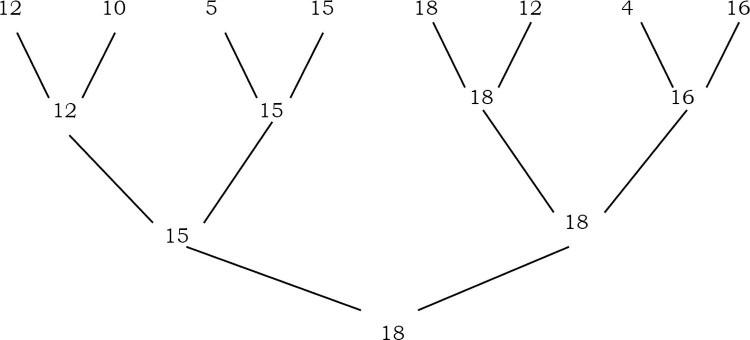
Để đơn giản, giả sử rằng các số là khác nhau và n là lũy thừa của 2. Chúng tôi ghép các khóa và so sánh các cặp theo vòng cho đến khi chỉ còn một vòng. Nếu đầu vào có tám keys, thì có bốn so sánh ở vòng đầu tiên, hai ở vòng thứ hai và một ở vòng cuối cùng. Người chiến thắng trong vòng cuối cùng là key lớn nhất. Hình dưới đây cho thấy phương pháp.
Phương pháp Tournament chỉ áp dụng khi n là lũy thừa của 2. Khi không xảy ra trường hợp này, chúng ta có thể thêm đủ các phần tử vào cuối mảng để làm cho kích thước mảng có lũy thừa là 2. Nếu cây đã hoàn thành thì chiều cao tối đa của cây là logn. Nếu chúng ta xây dựng cây nhị phân hoàn chỉnh, chúng ta cần so sánh n - 1 để tìm ra cây lớn nhất. Key lớn thứ hai phải nằm trong số những chiếc bị mất khi so sánh với key lớn nhất. Điều đó có nghĩa là, phần tử lớn thứ hai phải là một trong những đối thủ của phần tử lớn nhất. Số lượng key mà khóa lớn nhất đã so sánh là chiều cao của cây, tức là logn [nếu cây là cây nhị phân đầy đủ]. Sau đó, sử dụng thuật toán lựa chọn để tìm ra cái lớn nhất trong số chúng, hãy so sánh logn – 1. Như vậy tổng số lần so sánh để tìm key lớn nhất và lớn thứ hai là n + logn–2.
Các bạn có thể tham khảo thêm implement ở đây
All rights reserved