Problem-1

Cho một mảng n số, hãy nêu thuật toán kiểm tra xem trong mảng có phần tử nào trùng nhau hay không?

Solution: Đây là một trong những vấn đề đơn giản nhất. Một câu trả lời rõ ràng cho điều này là tìm kiếm triệt để các bản sao trong mảng. Điều đó có nghĩa là, đối với mỗi phần tử đầu vào, hãy kiểm tra xem có phần tử nào có cùng giá trị không. Điều này chúng ta có thể giải quyết chỉ bằng cách sử dụng hai vòng lặp for đơn giản. Mã cho giải pháp này có thể được đưa ra là:

    public void CheckDuplicatesBruteForce(int[] A){
        for (int i = 0; i < A.length; i++) {
            for (int j = 0; j < A.length; j++) {
                if(A[i] == A[j]){
                    System.out.println("Duplicates exist: " + A[i]);
                    return;
                }
            }
        }
        System.out.println("No duplicates in given array");
    }

Time Complexity: $O(n^2)$
Space Complexity: $O(1)$.

Problem-2

Chúng ta có thể cải thiện độ phức tạp của giải pháp của Problem-1 không?

Solution: Yes. Sắp xếp mảng đã cho. Sau khi sắp xếp, tất cả các phần tử có giá trị bằng nhau sẽ liền kề nhau. Bây giờ, hãy thực hiện một lần quét khác trên mảng đã sắp xếp này và xem liệu có phần tử nào có cùng giá trị và liền kề không.

    public void CheckDuplicatesSorting(int[] A){
        Arrays.sort(A);
        for (int i = 0; i < A.length-1; i++) {
            if(A[i] == A[i+1]){
                System.out.println("Duplicates exist: " + A[i]);
                return;
            }
        }
        System.out.println("No duplicates in given array");
    }

Time Complexity: $O(nlogn)$,
Space Complexity: $O(1)$.

Problem-3

Có cách nào khác để giải quyết Problem-1 không?

Solution: Yes, sử dụng hash table. Hash tables là một phương pháp đơn giản và hiệu quả được sử dụng để implement từ điển. Thời gian trung bình để tìm kiếm một phần tử là $O(1)$, trong khi thời gian trong trường hợp xấu nhất là $O(n)$. Chương về Hashing mình sẽ trình bày chi tiết về các thuật toán hashing. Ví dụ, xét mảng A = {3,2,1,2,2,3}.

Quét mảng đầu vào và chèn các phần tử vào hàm băm. Đối với mỗi phần tử được chèn, hãy giữ bộ đếm là 1 (giả sử ban đầu tất cả các phần tử được điền bằng số không). Điều này chỉ ra rằng phần tử tương ứng đã xảy ra rồi. Đối với mảng đã cho, bảng băm sẽ như thế nào (sau khi chèn ba phần tử đầu tiên 3,2 và 1):

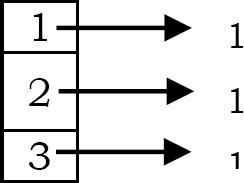
Bây giờ nếu chúng ta thử chèn 2, vì giá trị bộ đếm của 2 đã là 1, chúng ta có thể nói rằng phần tử đã xuất hiện hai lần.
Time Complexity: O(n). Space Complexity: O(n).

Problem-4

Chúng ta có thể cải thiện hơn nữa độ phức tạp của giải pháp Problem-1 không?

Solution: Giả sử rằng các phần tử mảng là số dương và tất cả các phần tử nằm trong khoảng từ 0 đến n – 1. Đối với mỗi phần tử A[i], hãy chuyển đến phần tử mảng có index là A[i]. Điều đó có nghĩa là chọn A[A[i]] và đánh dấu A[A[i]] (phủ định giá trị tại A[A[i]] ~ nghĩa là biến số đó thành âm). Tiếp tục quá trình này cho đến khi chúng ta gặp phần tử có giá trị đã bị phủ định. Nếu một phần tử như vậy tồn tại thì chúng ta nói các phần tử trùng lặp tồn tại trong mảng đã cho. Nếu một phần tử như vậy tồn tại thì chúng ta nói các phần tử trùng lặp tồn tại trong mảng đã cho. Ví dụ, xét mảng A = {3,2,1,2,2,3}.

Ban đầu,

Ở bước 1, phủ định A[abs(A[0])],

Ở bước 2, phủ định A[abs(A[1])],

Ở bước 3, phủ định A[abs(A[2])],

Ở bước 4, phủ định A[abs(A[3])],

Ở bước 4, quan sát rằng A[abs(A[3])] đã âm. Điều đó có nghĩa là chúng ta đã gặp phải cùng một giá trị hai lần.

    public void checkDuplicates(int[] A){
        for (int i = 0; i < A.length; i++) {
            if(A[Math.abs(A[i])] < 0){
                System.out.println("Duplicates exist: " + A[i]);
                return;
            }
        }
        System.out.println("No duplicates in given array");
    }

Time Complexity: O(n).
Space Complexity: O(1).

Notes:

• Giải pháp này không hoạt động nếu mảng đã cho ở chế độ chỉ đọc(Không được phép chỉnh sửa).
• Giải pháp này sẽ chỉ hoạt động nếu tất cả các phần tử mảng đều dương.
• Nếu phạm vi phần tử không nằm trong khoảng từ 0 đến n – 1 thì nó có thể ném ra các exceptions.

Problem-5

Cho một dãy n số. Hãy viết thuật toán tìm phần tử xuất hiện nhiều nhất trong mảng?

Brute Force Solution: Một giải pháp đơn giản cho vấn đề này là, đối với mỗi phần tử đầu vào, hãy kiểm tra xem có bất kỳ phần tử nào có cùng giá trị hay không và đối với mỗi lần xuất hiện như vậy, hãy tăng bộ đếm. Mỗi lần, kiểm tra bộ đếm hiện tại với bộ đếm tối đa và cập nhật nó nếu giá trị này lớn hơn bộ đếm tối đa. Điều này chúng ta có thể giải quyết chỉ bằng cách sử dụng hai vòng lặp for đơn giản.

    public int MaxRepititionsBruteForce(int[] A){
        int counter = 0, max = 0;
        for (int i = 0; i < A.length; i++) {
            counter = 0;
            for (int j = 0; j < A.length; j++) {
                if(A[i] == A[j]){
                    counter++;
                }
            }
            if(counter > max){
                max = counter;
            }
        }
        return max;
    }

Time Complexity: $O(n^2)$, cho 2 vòng lặp
Space Complexity: O(1).

Problem-6

Chúng ta có thể cải thiện độ phức tạp của giải pháp Problem-5 không?

Solution: Yes. Sắp xếp mảng đã cho. Sau khi sắp xếp, tất cả các phần tử có giá trị bằng nhau sẽ liền kề nhau. Bây giờ, chỉ cần thực hiện một lần quét khác trên mảng đã sắp xếp này và xem phần tử nào xuất hiện với số lần tối đa.

Time Complexity: $O(nlogn)$. (Dành cho sắp xếp).\ Space Complexity: $O(1)$.

Problem-7

Có cách nào khác để giải quyết Problem-5 không?

Solution: Yes, sử dụng hash table. Đối với mỗi phần tử của đầu vào, hãy theo dõi số lần phần tử đó xuất hiện trong đầu vào. Điều đó có nghĩa là giá trị bộ đếm đại diện cho số lần xuất hiện của phần tử đó.

Time Complexity: O(n). Space Complexity: O(n).

Problem-8

Đối với Problem-5, chúng ta có thể cải thiện độ phức tạp của thời gian không? Giả sử rằng phạm vi của các phần tử là từ 1 đến n. Điều đó có nghĩa là tất cả các phần tử chỉ nằm trong phạm vi này.

Solution: Yes. Chúng tôi có thể giải quyết vấn đề này trong hai lần quét. Chúng ta không thể sử dụng kỹ thuật phủ định của Vấn đề-3 cho vấn đề này vì số lần lặp lại. Trong lần quét đầu tiên, thay vì phủ định, hãy thêm giá trị n. Điều đó có nghĩa là đối với mỗi lần xuất hiện của một phần tử, hãy thêm kích thước mảng vào phần tử đó. Trong lần quét thứ hai, hãy kiểm tra giá trị phần tử bằng cách chia nó cho n và trả về phần tử mang lại giá trị lớn nhất. Mã dựa trên phương pháp này được đưa ra dưới đây.

    public int MaxRepitition(int[] A){
        int i = 0, max = 0, maxIndex = -1, n = A.length;
        for (int j = 0; j < n; j++) {
            A[A[i]%n] += n;
        }
        for (int j = 0; j < n; j++) {
            if(A[i]/n > max){
                max = A[i]/n;
                maxIndex = i;
            }
        }
        return maxIndex;
    }

Notes:

• Giải pháp này không hoạt động nếu mảng đã cho ở chế độ chỉ đọc(Không được phép chỉnh sửa).
• Giải pháp này sẽ chỉ hoạt động nếu tất cả các phần tử mảng đều dương.
• Nếu phạm vi phần tử không nằm trong khoảng từ 0 đến n – 1 thì nó có thể ném ra các exceptions.

Time Complexity: O(n). Vì không cần các vòng lặp lồng nhau.
Space Complexity: O(1).

Problem-9

Cho một mảng n số, hãy viết thuật toán tìm phần tử đầu tiên của mảng lặp lại. Ví dụ, trong mảng A = {3,2,1,2,2,3}, số lặp lại đầu tiên là 3 (không phải 2). Điều đó có nghĩa là, chúng ta cần trả về phần tử đầu tiên trong số các phần tử được lặp lại.

Solution: Chúng ta có thể sử dụng giải pháp brute force mà chúng ta đã sử dụng cho Problem-1. Đối với mỗi phần tử, vì nó kiểm tra xem phần tử đó có trùng lặp hay không nên phần tử nào trùng lặp trước sẽ được trả về.

Problem-10

Đối với Problem-9, chúng ta có thể sử dụng kỹ thuật sắp xếp không?

Solution: Không, Để chứng minh trường hợp thất bại, chúng ta hãy xem xét mảng sau. Ví dụ: A = {3, 2, 1, 2, 2, 3}. Sau khi sắp xếp ta được A={1,2,2,2,3,3}. Trong mảng được sắp xếp này, phần tử lặp lại đầu tiên là 2 nhưng câu trả lời thực sự là 3.

Problem-11

Đối với Problem-9, chúng ta có thể sử dụng hash table không?

Solution: Yes. Nhưng kỹ thuật băm đơn giản mà chúng tôi đã sử dụng cho Problem-3 sẽ không hoạt động. Ví dụ: nếu chúng ta coi mảng đầu vào là A = {3,2,1,2,3}, thì phần tử lặp lại đầu tiên là 3, nhưng sử dụng kỹ thuật băm đơn giản, chúng ta nhận được câu trả lời là 2. Ví dụ: nếu chúng ta coi mảng đầu vào là A = {3,2,1,2,3}, thì phần tử lặp lại đầu tiên là 3, nhưng sử dụng kỹ thuật hashing đơn giản, chúng ta nhận được câu trả lời là 2. Bây giờ chúng ta hãy thay đổi hành vi của bảng băm để chúng ta có được phần tử lặp lại đầu tiên. Giả sử, thay vì lưu trữ 1 giá trị, ban đầu chúng ta lưu trữ vị trí của phần tử trong mảng. Kết quả là bảng băm sẽ như thế nào (sau khi chèn 3,2 và 1):

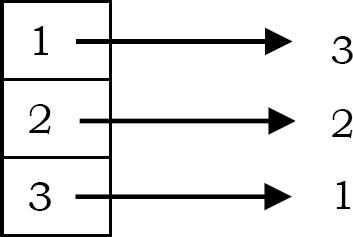
Bây giờ, nếu chúng ta thấy lại 2, chúng ta chỉ cần phủ nhận giá trị hiện tại của 2 trong bảng băm. Điều đó có nghĩa là, chúng tôi đặt giá trị bộ đếm của nó là –2. Giá trị âm trong bảng băm chỉ ra rằng chúng ta đã thấy cùng một phần tử hai lần. Tương tự, đối với 3 (phần tử tiếp theo trong đầu vào), chúng ta phủ định giá trị hiện tại của bảng băm và cuối cùng bảng băm sẽ như sau:

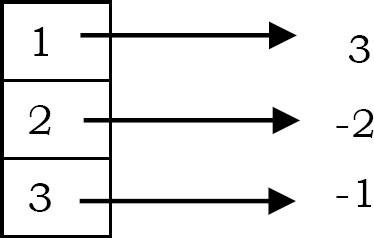
Sau khi xử lý mảng đầu vào hoàn chỉnh, hãy quét bảng băm và trả về giá trị được lập chỉ mục âm cao nhất từ nó (tức là –1 trong trường hợp của chúng ta). Giá trị âm cao nhất cho biết chúng ta đã nhìn thấy phần tử đó trước (trong số các phần tử được lặp lại) và cũng được lặp lại.

Điều gì xảy ra nếu phần tử được lặp lại nhiều hơn hai lần? Trong trường hợp này, chỉ cần bỏ qua phần tử nếu giá trị tương ứng i đã âm.

Problem-13

Tìm số còn thiếu: Chúng ta được cho một danh sách gồm n – 1 số nguyên và các số nguyên này nằm trong khoảng từ 1 đến n. Không có phần tử nào bị duplicate trong danh sách. Một trong những số nguyên bị thiếu trong danh sách. Đưa ra thuật toán tìm số nguyên còn thiếu.

Example: I/P:[1,2,4,6,3,7,8] O/P: 5

Solution: Một giải pháp đơn giản cho vấn đề này là, đối với mỗi số trong 1 đến n, hãy kiểm tra xem số đó có trong mảng đã cho hay không.

    public int FindMissingNumber(int[] A){
        int i,j, found = 0, n = A.length;
        for (i = 0; i < n; i++) {
            found = 0;
            for (j = 0; j < n; j++) {
                if(A[j] == i){
                    found = 1;
                }
            }
        }
        if(found != 0){
            return i;
        }
        return -1;
    }

Time Complexity: O(n2). Space Complexity: O(1).

Problem-14

Đối với Problem-13, chúng ta có thể sử dụng kỹ thuật sắp xếp không?

Solution: Yes. Việc sắp xếp danh sách sẽ cho các phần tử theo thứ tự tăng dần và với một lần quét khác, chúng ta có thể tìm thấy số còn thiếu.

Time Complexity: O(nlogn), cho việc sắp xếp. Space Complexity: O(1).

Problem-15

Đối với Problem-13, chúng ta có thể sử dụng kỹ thuật hashing không?

Solution: Yes. Quét mảng đầu vào và chèn các phần tử vào hàm băm. Đối với các phần tử được chèn, hãy giữ bộ đếm là 1 (giả sử ban đầu tất cả các phần tử được điền bằng số không). Điều này chỉ ra rằng phần tử tương ứng đã xảy ra rồi. Bây giờ, hãy quét bảng băm và trả về phần tử có giá trị bộ đếm bằng không.

Time Complexity: O(n). Space Complexity: O(n).

Problem-16

Đối với Problem-13, chúng ta có thể cải thiện độ phức tạp không?

Solution: Chúng ta có thể sử dụng công thức summation.

1. Lấy tổng các số, $sum = n × (n + l)/2$.
2. Trừ tất cả các số từ tổng và bạn sẽ nhận được số còn thiếu.

Time Complexity: O(n), cho việc scan toàn bộ mảng.

Problem-17

Trong Problem-13, nếu tổng các số vượt quá số nguyên tối đa cho phép, thì có thể xảy ra tràn số nguyên và chúng ta có thể không nhận được câu trả lời đúng. Chúng ta có thể giải quyết vấn đề này không?

Solution: Sử dụng phép dịch bit XOR

1. XOR tất cả các phần tử mảng, đặt kết quả của XOR là X.
2. XOR tất cả các số từ 1 đến n, đặt XOR là Y.
3. XOR của X và Y cho số còn thiếu.

Các bạn có thể tìm hiểu thêm về phép toán XOR ở đây,

Problem-18

Tìm số xuất hiện một số lần lẻ: Cho một dãy các số nguyên dương, tất cả các số đều xuất hiện với số lần chẵn, trừ một số xuất hiện với số lần lẻ. Tìm số trong O(n) time & constant space.

Example: I/P = [1,2,3,2,3,1,3] O/P = 3

Solution: Thực hiện phép dịch bit XOR tất cả các phần tử. Chúng tôi nhận được số có số lần xuất hiện lẻ. Điều này là do, A XOR A = 0.
Time Complexity: O(n). Space Complexity: O(1).