Problem-6

Tìm k phần tử nhỏ nhất trong mảng S gồm n phần tử.

Solution: Brute Force Approach: Quét qua các số k lần để có các phần tử mong muốn. Phương pháp này là phương pháp được sử dụng trong sắp xếp bong bóng (và sắp xếp lựa chọn), mỗi khi chúng ta tìm ra phần tử nhỏ nhất trong toàn bộ chuỗi bằng cách so sánh mọi phần tử. Trong phương pháp này, chuỗi phải được duyệt qua k lần. Vậy độ phức tạp là $O(n × k)$.

Problem-7

Chúng ta có thể sử dụng kỹ thuật sắp xếp để giải quyết Problem-6 không?

Solution: Yes. Sắp xếp và lấy k phần tử đầu tiên.

Sắp xếp n số là $O(nlogn)$ và chọn k phần tử là $O(k)$. Tổng độ phức tạp là $O(nlogn + k) = O(nlogn)$.

Problem-8

Chúng ta có thể sử dụng kỹ thuật tree sorting để giải Bài toán-6 không?

Solution: Yes.

1. Chèn tất cả các phần tử vào binary search tree.
2. Thực hiện duyệt InOrder và in k phần tử sẽ là phần tử nhỏ nhất. Vậy ta có k phần tử nhỏ nhất.

Chi phí tạo cây tìm kiếm nhị phân có n phần tử là O(nlogn) và duyệt tới k phần tử là O(k). Do đó độ phức tạp là $O(nlogn + k) = O(nlogn)$.

Điều bất lợi: Nếu các số được sắp xếp theo thứ tự giảm dần, chúng ta sẽ nhận được một cái cây lệch về bên trái. Trong trường hợp đó, cấu trúc của cây sẽ là $0 + l + 2 + ... + (n– 1) = \frac { n ( n - 1 ) } { 2 }$ là $O(n^2)$. Để tránh khỏi điều này, chúng ta có thể giữ cho cây cân bằng, do đó chi phí xây dựng cây sẽ chỉ là nlogn.

Về Tree, các bạn có thể xem lại trong 2 bài viết ở đây và ở đây

Problem-9

Chúng ta có thể cải thiện kỹ thuật tree sorting để giải Problem-6 không?

Solution: Yes. Sử dụng một cây nhỏ hơn để cho kết quả tương tự.

1. Lấy k phần tử đầu tiên của dãy để tạo balanced tree(cây cân bằng) gồm k nút (điều này sẽ tốn klogk).

2. Lấy lần lượt các số còn lại và

   • Nếu số lớn hơn phần tử lớn nhất của cây, hãy trả về.
   • Nếu số nhỏ hơn phần tử lớn nhất của cây thì loại bỏ phần tử lớn nhất của cây và thêm phần tử mới. Bước này nhằm đảm bảo rằng một phần tử nhỏ hơn sẽ thay thế một phần tử lớn hơn từ cây. Và tất nhiên, chi phí của hoạt động này là logk vì cây là cây cân bằng gồm k phần tử.

Khi Bước 2 kết thúc, cây cân bằng có k phần tử sẽ có k phần tử nhỏ nhất. Công việc còn lại chỉ là in ra phần tử lớn nhất của cây.

Time Complexity:

1. Đối với k phần tử đầu tiên, chúng ta tạo cây. Do đó chi phí là $klogk$.
2. Với n – k phần tử còn lại, độ phức tạp là $O(logk)$.

Bước 2 có độ phức tạp là $(n – k) logk$. Tổng chi phí là $klogk + (n – k) logk = nlogk$ là $O(nlogk)$. Giới hạn này thực sự tốt hơn những giới hạn được cung cấp trước đó.

Problem-10

Chúng ta có thể sử dụng kỹ thuật phân vùng để giải quyết Problem-6 không?

Solution: Yes.

Algorithm

1. Chọn một điểm làm trục từ mảng.
2. Phân vùng mảng sao cho: $A[low...pivotpoint – 1] <= pivotpoint <= A[pivotpoint + 1..high].$
3. nếu k < pivotpoint(điểm xoay) thì nó phải ở bên trái của trục, do đó, thực hiện đệ quy tương tự ở phần bên trái.
4. nếu k = Pivotpoint thì đó phải là Pivot và in tất cả các phần tử từ low đến Pivotpoint.
5. nếu k > pivotpoint thì nó phải ở bên phải của trục, do đó, thực hiện đệ quy tương tự ở phần bên phải.

import java.util.*;
 
class GFG {
 
    // Standard partition process of QuickSort.
    // It considers the last element as pivot
    // and moves all smaller element to left of
    // it and greater elements to right
    public static int partition(int arr[], int l, int r)
    {
        int x = arr[r], i = l;
        for (int j = l; j <= r - 1; j++) {
            if (arr[j] <= x) {
 
                // Swapping arr[i] and arr[j]
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
 
                i++;
            }
        }
 
        // Swapping arr[i] and arr[r]
        int temp = arr[i];
        arr[i] = arr[r];
        arr[r] = temp;
 
        return i;
    }
 
    // This function stops at k'th smallest element
    // in arr[l..r] using QuickSort based method.
 
    public static void kthSmallest(int arr[], int l, int r,
                                   int K, int N)
    {
        // If k is smaller than number of elements
        // in array
        if (K > 0 && K <= r - l + 1) {
 
            // Partition the array around last
            // element and get position of pivot
            // element in sorted array
            int pos = partition(arr, l, r);
 
            // If position is same as k
            if (pos - l == K - 1)
                return;
 
            // If position is more, recur for
            // left subarray
            if (pos - l > K - 1)
                kthSmallest(arr, l, pos - 1, K, N);
 
            // Else recur for right subarray
            else
                kthSmallest(arr, pos + 1, r,
                            K - pos + l - 1, N);
        }
        else {
            // If k is more than number of elements
            // in array
            System.out.print("Invalid value of K");
        }
    }
 
    public static void kthLargest(int arr[], int l, int r,
                                  int K, int N)
    {
        // This function arranges k Largest elements in last
        // k positions
        // It means it arranges N-K-1 smallest elements from
        // starting
 
        kthSmallest(arr, l, r, N - K - 1, N);
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int a[]
            = { 11, 3, 2, 1, 15, 5, 4, 45, 88, 96, 50, 45 };
        int n = a.length;
 
        int low = 0;
        int high = n - 1;
 
        // Lets assume k is 3
        int k = 3;
 
        // Function call
 
        // For Smallest
        kthSmallest(a, 0, n - 1, k, n);
 
        // Print KSmallest no.
        if (k >= 1 && k <= n) {
            System.out.print(k
                             + " smallest elements are : ");
            for (int i = 0; i < k; i++)
                System.out.print(a[i] + " ");
        }
        System.out.println();
 
        // For Largest
 
        kthLargest(a, 0, n - 1, k, n);
 
        // Print KLargest no.
        if (k >= 1 && k <= n) {
            System.out.print(k
                             + " largest elements are : ");
            for (int i = n - 1; i >= n - k; i--)
                System.out.print(a[i] + " ");
        }
    }
}

Code mình tham khảo ở đây

Time Complexity: $O(n^2)$ trong trường hợp xấu nhất tương tự như Quicksort. Mặc dù trường hợp xấu nhất giống với trường hợp của Quicksort, nhưng trường hợp trung bình thì hoạt động tốt hơn $O(nlogk)$

Problem-11

Chúng ta có thể tìm thấy phần tử lớn thứ k bằng cách sử dụng giải pháp Bài toán-6 không?

Solution: Tính toán phần tử lớn thứ k là cùng một nhiệm vụ, với sự khác biệt duy nhất là chúng ta phải dịch giá trị k, vì các phần tử lớn nhất nằm ở cuối mảng. Vì vậy, chúng tôi sẽ phải dịch k bằng công thức này: k = A.length – k + 1.

Problem-12

Tìm phần tử nhỏ thứ k trong mảng S gồm n phần tử theo cách tốt nhất có thể.

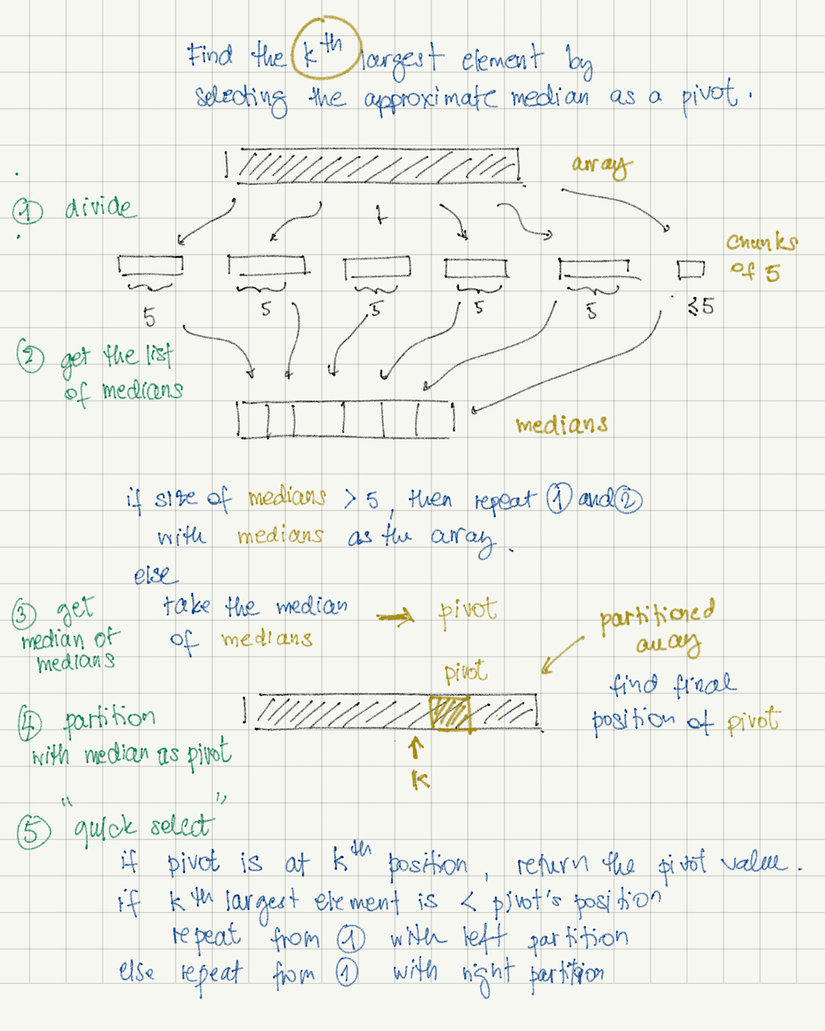
Solution: Vấn đề này tương tự như Vấn đề-6 và tất cả các giải pháp được thảo luận cho Vấn đề-6 đều hợp lệ cho vấn đề này. Sự khác biệt duy nhất là thay vì in tất cả k phần tử, chúng ta chỉ in phần tử thứ k. Chúng ta có thể cải thiện giải pháp bằng cách sử dụng median of medians algorithm(thuật toán trung vị của trung vị). Trung vị là một trường hợp đặc biệt của thuật toán lựa chọn. Thuật toán Selection(A, k) để tìm phần tử nhỏ thứ k từ tập A gồm n phần tử như sau:

Algorithm: Selection(A, k)

1. Phân vùng A trở thành $ceil ( \frac { l e n g t h ( A ) } { 5 } )$ nhóm, với mỗi nhóm có năm phần tử (nhóm cuối cùng có thể có ít phần tử hơn).
2. Sắp xếp riêng từng nhóm (ví dụ: sử dụng insertion sort).
3. Tìm trung vị của mỗi nhóm và lưu trữ chúng trong một số mảng (giả sử A′).
4. Sử dụng đệ quy Selection để tìm trung vị của A′ (trung vị của trung vị). Giả sử trung vị của trung vị là m.

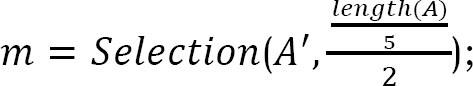
5. Cho q = số phần tử của A nhỏ hơn m;
6. If(k == q + 1)

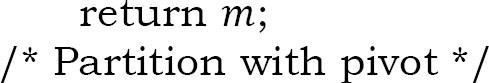
7. Else phân vùng A thành X và Y
   • X = {số phần tử nhỏ hơn m}
   • Y = {số phần tử lớn hơn m}
8. If(k < q + 1)

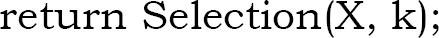
9. Else

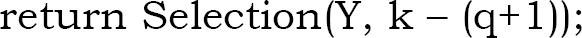
Example: Chúng ta hãy xem xét ví dụ minh họa bên dưới. Trong hình, mỗi vòng tròn là một phần tử và mỗi cột được nhóm 5 phần tử. Các vòng tròn màu đen biểu thị trung vị trong mỗi nhóm 5 phần tử. Như đã thảo luận, hãy sắp xếp từng cột bằng insertion sort theo thời gian không đổi.

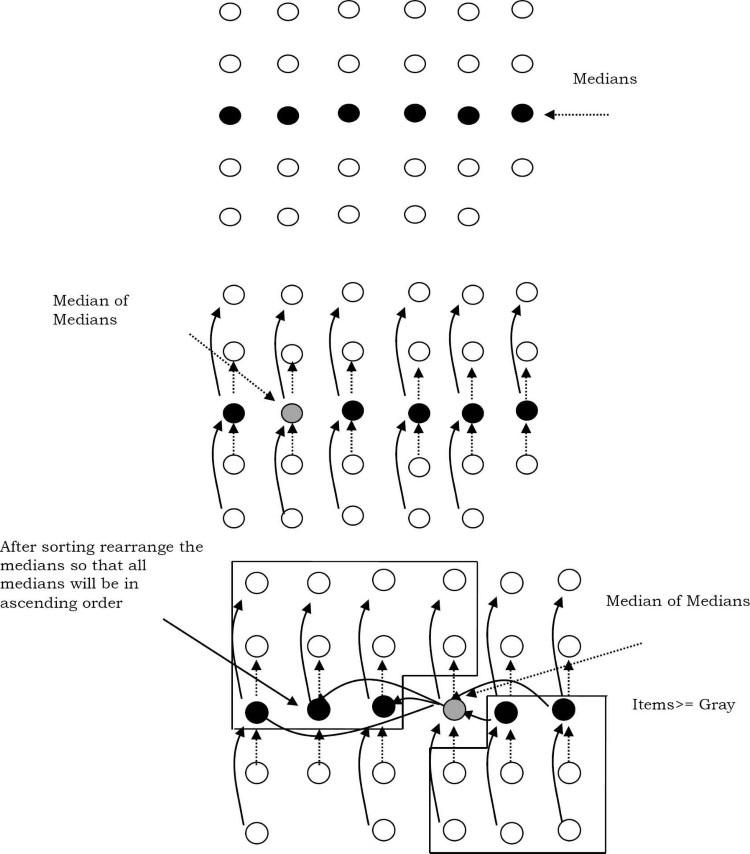
Trong hình trên, mục được khoanh tròn màu xám là trung vị của các trung vị (hãy gọi đây là m). Có thể thấy rằng ít nhất một nửa của các nhóm 5 phần tử ≤ m. Ngoài ra, 1/2 trong số các nhóm 5 phần tử này đóng góp 3 phần tử ≤ m ngoại trừ 2 nhóm [nhóm cuối cùng có thể chứa ít hơn 5 phần tử và nhóm còn lại chứa m]. Tương tự, ít nhất 1/2 trong số các nhóm 5 phần tử đóng góp 3 phần tử ≥ m như hình trên. 1/2 trong 5 nhóm nguyên tố góp 3 nguyên tố, trừ 2 phần tử lớn hơn trung vị: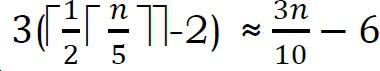

Còn lại là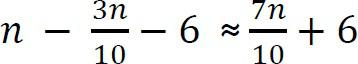

Vì 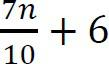lớn hơn

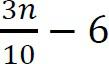
chúng ta cần xem xét 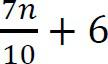cho trường hợp tồi tệ nhất.

Các thành phần trong đệ quy:

• Trong thuật toán lựa chọn của chúng ta, chúng ta chọn m, là trung vị của các trung vị, làm trục và phân chia A thành hai tập hợp X và Y. Chúng ta cần chọn tập hợp có kích thước tối đa (để tránh trường hợp xấu nhất).
• Thời gian trong function Selection khi được gọi khi phân vùng. Số lượng phần tử trong đầu vào khi gọi tới Selection là $\frac { n } { 5 }$.
• Số phép so sánh cần thiết để phân vùng mảng. Con số này là S.length, giả sử n.

Chúng ta đã thiết lập đệ quy sau đây:

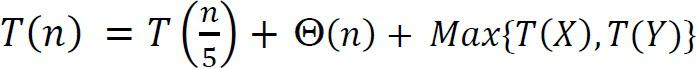
Từ cuộc thảo luận ở trên, chúng ta đã thấy rằng, nếu chúng ta chọn trung vị của trung vị m làm trục, kích thước phân vùng là: $\frac { 3 n } { 1 0 } - 6$ và $\frac { 7 n } { 1 0 } + 6$. Nếu chúng ta chọn tối đa trong số này, thì chúng ta nhận được:

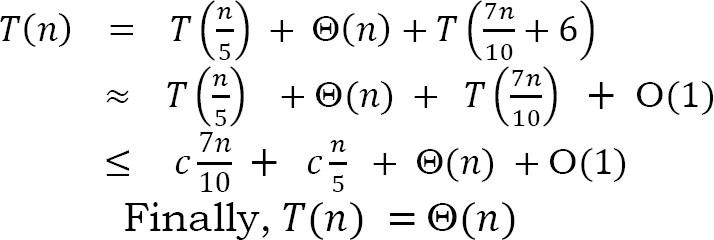
Hình ảnh mình tham khảo ở đây, code mình tham khảo ở đây

package SelectionAlgorithms;
import java.util.Arrays;

/* Name of the class has to be "Main" only if the class is public. */
class MedianOfMedians {
    public static void main(String[] args) throws java.lang.Exception {
        int[] arr = new int[] { 7, 15, 4, 3, 20, 10 };
        System.out.println("kth smallest in the given array is "
                + getKthSmallestQuickSelectWorstCaseLinearTime(arr, 0, arr.length - 1, 4));
    }

    private static int getKthSmallestQuickSelectWorstCaseLinearTime(int arr[], int low, int high, int k) {

        if (k > 0 && k <= high - low + 1) {
            // number of elements in array
            int n = high - low + 1;

            int i, median[] = new int[(n + 4) / 5];

            for (i = 0; i < median.length - 1; i++) {
                median[i] = getMedian(Arrays.copyOfRange(arr, 5 * i + low, 5 * i + low + 4), 5);
            }

            if (n % 5 == 0) {
                median[i] = getMedian(Arrays.copyOfRange(arr, 5 * i + low, 5 * i + low + 4), 5);
                i++;
            } else {
                median[i] = getMedian(Arrays.copyOfRange(arr, 5 * i + low, 5 * i + low + (n % 5)), n % 5);
                i++;
            }

            int medOfMed = i == 1 ? median[i - 1]
                    : getKthSmallestQuickSelectWorstCaseLinearTime(median, 0, i - 1, i / 2);

            int partition = partitionPractise(arr, low, high, medOfMed);

            if (partition - low == k - 1) {
                return arr[partition];
            }

            if (partition - low > k - 1) {
                return getKthSmallestQuickSelectWorstCaseLinearTime(arr, low, partition - 1, k);
            }

            return getKthSmallestQuickSelectWorstCaseLinearTime(arr, partition + 1, high, k - (partition + 1) + low);
        }

        return -1;
    }

    private static int getMedian(int arr[], int n) {
        Arrays.sort(arr);
        return arr[n / 2];
    }




    private static void swap(int[] arr, int i, int index) {
        if (arr[i] == arr[index]) {
            return;
        }
        int temp = arr[i];
        arr[i] = arr[index];
        arr[index] = temp;
    }

    private static int partitionPractise(int[] arr, int low, int high, int pivot) {

        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == pivot) {
                swap(arr, i, high);
                break;
            }
        }
        int index = low - 1;
        int i = low;
        while (i < high) {
            if (arr[i] < pivot) {
                index++;
                swap(arr, i, index);
            }
            i++;
        }
        index++;
        swap(arr, index, high);
        return index;
    }

}