10.1 Sorting là gì?

Sorting(Sắp xếp) là một thuật toán sắp xếp các phần tử của danh sách theo một thứ tự nhất định [tăng dần hoặc giảm dần]. Đầu ra là một hoán vị hoặc sắp xếp lại đầu vào.

10.2 Tại sao việc sắp xếp lại cần thiết?

Sắp xếp là một trong những loại thuật toán quan trọng trong khoa học máy tính và rất nhiều nghiên cứu về chủ đề này. Sắp xếp có thể làm giảm đáng kể độ phức tạp của một vấn đề và thường được sử dụng cho các thuật toán và tìm kiếm cơ sở dữ liệu.

10.3 Phân loại thuật toán sắp xếp

Các thuật toán sắp xếp thường được phân loại dựa trên các tham số sau.

Theo số lần so sánh

Trong phương pháp này, các thuật toán sắp xếp được phân loại dựa trên số lần so sánh. Đối với các thuật toán sắp xếp dựa trên so sánh, hành vi trường hợp tốt nhất là $O(nlogn)$ và hành vi trường hợp xấu nhất là $O(n^2)$. Các thuật toán sắp xếp dựa trên so sánh đánh giá các phần tử của danh sách bằng thao tác so sánh key và cần ít nhất phép so sánh $O(nlogn)$ cho hầu hết các đầu vào.

Ở phần sau của chương này, chúng ta sẽ thảo luận về một vài thuật toán sắp xếp phi so sánh (tuyến tính) như Counting sort, Bucket sort, Radix sort, v.v. Linear Sorting(Các thuật toán Sắp xếp tuyến tính) áp đặt một số hạn chế đối với đầu vào để cải thiện độ phức tạp.

Theo số lần hoán đổi

Trong phương pháp này, các thuật toán sắp xếp được phân loại theo số lần hoán đổi (còn gọi là nghịch đảo).

Theo cách sử dụng bộ nhớ

Một số thuật toán sắp xếp là “tại chỗ” và chúng cần bộ nhớ O(1) hoặc O(logn) để tạo các vị trí phụ trợ để sắp xếp dữ liệu tạm thời.

Bằng đệ quy

Các thuật toán sắp xếp là đệ quy [quick sort] hoặc không đệ quy [selection sort, and insertion sort] và có một số thuật toán sử dụng cả hai (sắp xếp hợp nhất merge sort).

Theo khả năng thích ứng(Adaptive)

Với một vài thuật toán sắp xếp, độ phức tạp thay đổi dựa trên độ sắp xếp trước [quick sort]: độ sắp xếp trước của đầu vào ảnh hưởng đến thời gian chạy. Các thuật toán có tính đến điều này được coi là thích ứng.

10.4 Các phân loại khác

Một phương pháp khác để phân loại các thuật toán sắp xếp là:

• Internal Sort
• External Sort

Internal Sort

Thuật toán sắp xếp chỉ sử dụng bộ nhớ chính trong quá trình sắp xếp được gọi là thuật toán sắp xếp bên trong. Loại thuật toán này giả định truy cập ngẫu nhiên tốc độ cao vào tất cả bộ nhớ.

External Sort

Các thuật toán sắp xếp sử dụng bộ nhớ ngoài, chẳng hạn như băng hoặc đĩa, trong quá trình sắp xếp thuộc danh mục này.

10.5 Bubble Sort

Bubble sort là thuật toán sắp xếp đơn giản nhất. Nó hoạt động bằng cách lặp lại mảng đầu vào từ phần tử đầu tiên đến phần tử cuối cùng, so sánh từng cặp phần tử và hoán đổi chúng nếu cần. Bubble sort tiếp tục lặp đi lặp lại cho đến khi không cần hoán đổi nữa. Thuật toán được đặt tên theo cách các phần tử nhỏ hơn “bubble(nổi)” lên đầu danh sách. Nói chung, insertion sort có hiệu suất tốt hơn so với bubble sort. Một số nhà nghiên cứu gợi ý rằng chúng ta không nên dạy sắp xếp bong bóng vì tính đơn giản và độ phức tạp cao về thời gian của nó. Ưu điểm đáng kể duy nhất mà bubble sort có so với các triển khai khác là nó có thể phát hiện xem danh sách đầu vào đã được sắp xếp hay chưa.

Implementation

public void BubbleSort(int A[]){
        for(int pass = A.length-1; pass >= 0; pass--){
            for(int i = 0; i <= pass-1; i++){
                if(A[i] > A[i+1]){
                    //swap elements
                    int temp = A[i];
                    A[i] = A[i+1];
                    A[i+1] = temp;
                }
            }
        }
    }

Thuật toán lấy $O(n^2)$ (ngay cả trong trường hợp tốt nhất). Chúng ta có thể cải thiện nó bằng cách sử dụng thêm một lá cờ. Không còn hoán đổi nào cho thấy việc sắp xếp đã hoàn tất. Nếu danh sách đã được sắp xếp, chúng ta có thể sử dụng cờ này để bỏ qua các lượt còn lại.

    public void BubbleSortImproved(int[] A){
        int pass, i, temp, swapped = 1;
        for(pass = A.length-1; pass >= 0 && swapped == 1; pass--){
            swapped = 0;
            for(i = 0; i <= pass-1; i++){
                if(A[i] > A[i+1]){
                    //swap elements
                    temp = A[i];
                    A[i] = A[i+1];
                    A[i+1] = temp;
                    swapped = 1;
                }
            }
        }
    }

Phiên bản sửa đổi này cải thiện trường hợp bubble sort tốt nhất thành O(n).

Performance

10.6 Selection Sort

Selection Sort(Sắp xếp lựa chọn) là một thuật toán sắp xếp tại chỗ. Sắp xếp lựa chọn hoạt động tốt cho các tệp nhỏ. Nó được sử dụng để sắp xếp các tệp có giá trị rất lớn và các khóa nhỏ.

Điều này là do lựa chọn được thực hiện dựa trên các khóa và các hoán đổi chỉ được thực hiện khi được yêu cầu.

Ưu điểm

• Dễ để implement
• Sắp xếp tại chỗ (không yêu cầu thêm dung lượng lưu trữ)

Nhược điểm

• Độ phức tạp cao: $O(n^2)$

Thuật toán

1. Tìm giá trị nhỏ nhất trong danh sách
2. Hoán đổi nó với giá trị ở vị trí hiện tại
3. Lặp lại quá trình này cho tất cả các phần tử cho đến khi toàn bộ mảng được sắp

Thuật toán này được gọi là sắp xếp lựa chọn vì nó lặp đi lặp lại việc chọn phần tử nhỏ nhất(hoặc lớn nhất).

Implementation

    public void SelectionSort(int[] A){
        int i, j, min, temp;
        for(i=0; i < A.length-1; i++){
            min = i;
            for(j = i+1; j < A.length; j++){
                if(A[j] < A[min]){
                    min = j;
                }
            }
            //swap elements
            temp = A[min];
            A[min] = A[i];
            A[i] = temp;
        }
    }

Performance

10.7 Insertion Sort

Insertion sort là một loại so sánh đơn giản và hiệu quả. Trong thuật toán này, mỗi lần lặp lại loại bỏ một phần tử khỏi dữ liệu đầu vào và chèn nó vào đúng vị trí trong danh sách được sắp xếp. Việc lựa chọn phần tử bị xóa khỏi đầu vào là ngẫu nhiên và quá trình này được lặp lại cho đến khi tất cả các phần tử đầu vào đã đi qua.

Ưu điểm

• Dễ để implement
• Hiệu quả cho dữ liệu nhỏ
• Adaptive(Thích nghi): Nếu danh sách đầu vào được sắp xếp trước [có thể không hoàn toàn] thì sắp xếp các phép chèn sẽ lấy O(n + d), trong đó d là số phép nghịch đảo
• Thực tế hiệu quả hơn so với các loại selection và bubble sorts, mặc dù tất cả chúng đều có độ phức tạp trong trường hợp xấu nhất là $O(n^2)$
• In-place: Nó chỉ yêu cầu một lượng không đổi O(1) dung lượng bộ nhớ bổ sung
• ...

Algorithm

Mỗi lần lặp lại insertion sort sẽ loại bỏ một phần tử khỏi dữ liệu đầu vào và chèn nó vào đúng vị trí trong danh sách đã được sắp xếp cho đến khi không còn phần tử đầu vào nào. Sắp xếp thường được thực hiện tại chỗ. Mảng kết quả sau k lần lặp có thuộc tính trong đó k + 1 mục đầu tiên được sắp xếp.

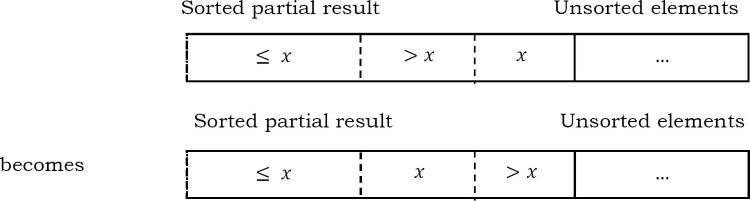
Mỗi phần tử lớn hơn x được sao chép sang bên phải khi nó được so sánh với x.

    public void InsertionSort(int[] A){
        int i,j,v;
        for(i = 1; i <= A.length; i++){
            v = A[i];
            j = i;
            while(A[j-1] > v && j >= 1){
                A[j] = A[j-1];
                j--;
            }
            A[j] = v;
        }
    }

Example

Cho một mảng: 6 8 1 4 5 3 7 2 và mục tiêu là sắp xếp chúng theo thứ tự tăng dần.

Phân tích

Worst case analysis Trường hợp xấu nhất xảy ra khi với mỗi i vòng lặp bên trong phải di chuyển tất cả các phần tử A[1], . . . , A[i – 1] (xảy ra khi giá trị A[i] = nhỏ hơn tất cả chúng), mất $Θ(i – 1)$ thời gian.

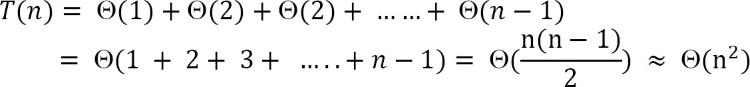
Average case analysis Đối với trường hợp trung bình, vòng lặp bên trong sẽ chèn A[i] vào giữa A[1], . . . , A[i – 1]. Điều này mất $Θ(i/2)$ thời gian.

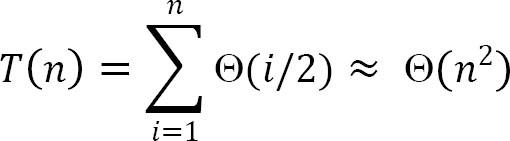
Performance

Nếu mọi phần tử đều lớn hơn hoặc bằng mọi phần tử bên trái nó, thì thời gian thực hiện của sắp xếp chèn là Θ(n). Tình huống này xảy ra nếu mảng bắt đầu đã được sắp xếp và do đó, một mảng đã được sắp xếp là trường hợp tốt nhất để sắp xếp chèn.

So sánh với các thuật toán sắp xếp khác

Sắp xếp chèn là một trong những thuật toán sắp xếp cơ bản với thời gian xấu nhất là $O(n^2)$. Sắp xếp chèn được sử dụng khi dữ liệu gần được sắp xếp (do tính thích ứng của nó) hoặc khi kích thước đầu vào nhỏ (do chi phí thấp). Vì những lý do này và do tính ổn định của nó, sắp xếp chèn được sử dụng làm trường hợp cơ sở đệ quy (khi kích thước vấn đề nhỏ) cho các thuật toán sắp xếp chia để trị chi phí cao hơn, chẳng hạn như merge sort hoặc quick sort.

Lưu ý:

• Bubble sort thực hiện $n^2/2$ phép so sánh và $n^2/2$ phép hoán đổi (nghịch đảo) trong cả trường hợp trung bình và trường hợp xấu nhất.
• Selection sort thực hiện $n^2/2$ phép so sánh và n phép hoán đổi.
• Insertion sort có $n^2/4$ các phép so sánh và $n^2/8$ các phép hoán đổi trong trường hợp trung bình và trong trường hợp xấu nhất chúng là gấp đôi.
• Insertion sort gần như tuyến tính đối với đầu vào được sắp xếp một phần.

10.8 Shell Sort

Shell Sort (còn gọi là sắp xếp tăng dần giảm dần) được phát minh bởi Donald Shell. Thuật toán sắp xếp này là sự tổng quát hóa của insertion sort. insertion sort hoạt động hiệu quả trên đầu vào đã được sắp xếp gần hết. Shell sort còn được gọi là n-gap insertion sort. Thay vì chỉ so sánh cặp liền kề, Shell sort thực hiện một số lần và sử dụng các gaps khác nhau giữa các phần tử liền kề (kết thúc bằng gap 1 hoặc insertion sort cổ điển).

Trong insertion sort, so sánh được thực hiện giữa các phần tử liền kề. Loại bỏ tối đa 1 phép đảo ngược cho mỗi phép so sánh được thực hiện với sắp xếp chèn. Biến thể được sử dụng trong shell sort là để tránh so sánh các phần tử liền kề cho đến bước cuối cùng của thuật toán. Vì vậy, bước cuối cùng của sắp xếp shell thực sự là thuật toán insertion sort. Nó cải thiện insertion sort bằng cách cho phép so sánh và trao đổi các phần tử ở xa. Đây là thuật toán đầu tiên có độ phức tạp nhỏ hơn bậc hai trong số các thuật toán sắp xếp so sánh.

Shellsort thực sự là một phần mở rộng đơn giản cho sắp xếp chèn. Sự khác biệt chính là khả năng trao đổi các phần tử cách xa nhau, giúp các phần tử đến vị trí của chúng nhanh hơn đáng kể. Ví dụ: nếu phần tử nhỏ nhất nằm ở cuối mảng, thì với sắp xếp chèn, nó sẽ yêu cầu toàn bộ mảng các bước để đặt phần tử này ở đầu mảng. Tuy nhiên, với sắp xếp vỏ, phần tử này có thể nhảy nhiều bước một lần và đến đích thích hợp trong ít lần trao đổi hơn.

Ý tưởng cơ bản trong shellsort là trao đổi mọi phần tử thứ h trong mảng. Bây giờ điều này có thể gây nhầm lẫn vì vậy chúng ta sẽ nói nhiều hơn về điều này, h xác định mức độ trao đổi phần tử cách xa nhau có thể xảy ra, ví dụ: lấy h là 13, phần tử đầu tiên (index-0) được trao đổi với phần tử thứ 14 (index-13 ) nếu cần thiết (tất nhiên). Phần tử thứ hai với phần tử thứ 15, v.v. Bây giờ nếu chúng ta lấy h bằng 1, thì nó hoàn toàn giống như một sắp xếp chèn thông thường.

Shellsort hoạt động bằng cách bắt đầu với h đủ lớn (nhưng không lớn hơn kích thước mảng) để cho phép trao đổi các phần tử đủ điều kiện cách xa nhau. Sau khi sắp xếp hoàn tất với một h cụ thể, mảng có thể được gọi là sắp xếp theo h. Bước tiếp theo là giảm h theo một trình tự nhất định và lại thực hiện một lần sắp xếp h hoàn chỉnh khác. Khi h là 1 và được sắp xếp h, mảng được sắp xếp hoàn toàn. Lưu ý rằng chuỗi cuối cùng của ft là 1 nên sắp xếp cuối cùng luôn là sắp xếp chèn, ngoại trừ vào thời điểm này mảng đã được định dạng tốt và dễ sắp xếp hơn.

Shell sort sử dụng một dãy h1,h2, ...,ht được gọi là dãy tăng dần. Bất kỳ chuỗi tăng nào cũng được miễn là h1 = 1 và một số lựa chọn tốt hơn những lựa chọn khác. Shell sort thực hiện nhiều lần duyệt qua danh sách đầu vào và sắp xếp một số tập hợp có kích thước bằng nhau bằng cách sử dụng insertion sort. Shell sort cải thiện hiệu quả của insertion sort bằng cách nhanh chóng chuyển các giá trị đến đích của chúng.

Code mình tham khảo ở đây

class ShellSort
{
    /* An utility function to print array of size n*/
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i=0; i<n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
  
    /* function to sort arr using shellSort */
    int sort(int arr[])
    {
        int n = arr.length;
  
        // Start with a big gap, then reduce the gap
        for (int gap = n/2; gap > 0; gap /= 2)
        {
            // Do a gapped insertion sort for this gap size.
            // The first gap elements a[0..gap-1] are already
            // in gapped order keep adding one more element
            // until the entire array is gap sorted
            for (int i = gap; i < n; i += 1)
            {
                // add a[i] to the elements that have been gap
                // sorted save a[i] in temp and make a hole at
                // position i
                int temp = arr[i];
  
                // shift earlier gap-sorted elements up until
                // the correct location for a[i] is found
                int j;
                for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
                    arr[j] = arr[j - gap];
  
                // put temp (the original a[i]) in its correct
                // location
                arr[j] = temp;
            }
        }
        return 0;
    }
  
    // Driver method
    public static void main(String args[])
    {
        int arr[] = {12, 34, 54, 2, 3};
        System.out.println("Array before sorting");
        printArray(arr);
  
        ShellSort ob = new ShellSort();
        ob.sort(arr);
  
        System.out.println("Array after sorting");
        printArray(arr);
    }
} 

Lưu ý rằng khi gap == 1, thuật toán sẽ chuyển qua toàn bộ danh sách, so sánh các phần tử liền kề, nhưng thực hiện rất ít trao đổi phần tử. Đối với gap == 1, sắp xếp hệ vỏ hoạt động giống như sắp xếp chèn, ngoại trừ số lượng phép đảo ngược phải loại bỏ được giảm đáng kể nhờ các bước trước đó của thuật toán với gap > 1.

Phân tích

Shell sort hiệu quả cho các danh sách kích thước trung bình. Đối với các danh sách lớn hơn, thuật toán không phải là lựa chọn tốt nhất. Đây là thuật toán sắp xếp nhanh nhất trong tất cả các thuật toán sắp xếp $O(n^2)$. Nhược điểm của shell sort là nó là một thuật toán phức tạp và gần như không hiệu quả bằng merge, heap, và quick sorts. Nó là một lựa chọn tốt để sắp xếp danh sách dưới 5000 mục trừ khi tốc độ là quan trọng. Nó cũng là một lựa chọn tốt để sắp xếp lặp đi lặp lại các danh sách nhỏ hơn. Trường hợp tốt nhất trong Shell sort là khi mảng đã được sắp xếp theo đúng thứ tự. Số lượng so sánh ít hơn. Thời gian chạy của Shell sort phụ thuộc vào sự lựa chọn trình tự tăng dần.

Performance

10.9 Merge Sort

Merge sort là một ví dụ về chiến lược chia để trị.

Ghi chú quan trọng

• Merging là quá trình kết hợp hai tệp được sắp xếp để tạo thành một tệp được sắp xếp lớn hơn.
• Selection là quá trình chia một tập tin thành hai phần: k phần tử nhỏ nhất và n – k phần tử lớn nhất.
• Selection and merging là các hoạt động ngược nhau
  • Selection chia danh sách thành hai danh sách
  • Merging nối hai tệp để tạo thành một tệp
• Merge sort là bổ sung của Quick sort
• Merge sort truy cập dữ liệu theo cách tuần tự
• Thuật toán này dùng để sắp xếp danh sách liên kết
• Merge sort không nhạy cảm với thứ tự ban đầu của đầu vào của nó
• Merge sort chia danh sách thành hai phần; sau đó từng phần được chinh phục riêng lẻ. Merge sort bắt đầu với các tệp con nhỏ và kết thúc với tệp con lớn nhất. Kết quả là nó không cần thêm Stack. Thuật toán này ổn định.

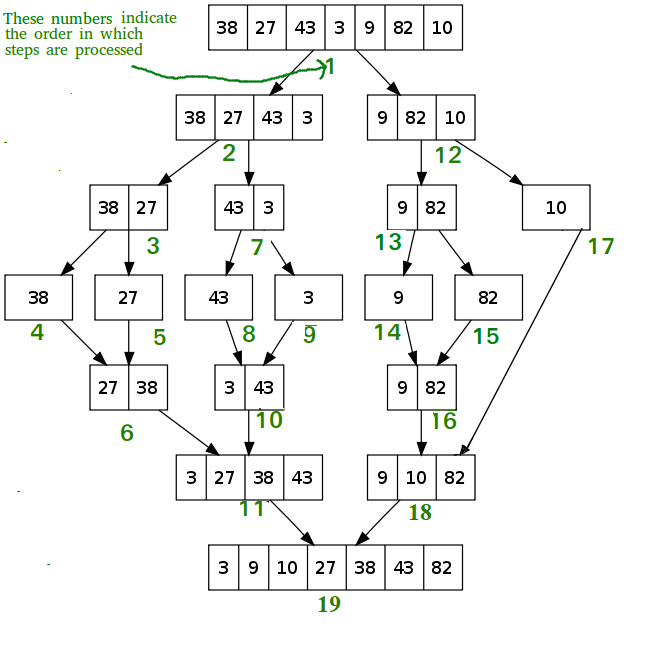
Code mình tham khảo ở đây

class MergeSort {
    // Merges two subarrays of arr[].
    // First subarray is arr[l..m]
    // Second subarray is arr[m+1..r]
    void merge(int arr[], int l, int m, int r)
    {
        // Find sizes of two subarrays to be merged
        int n1 = m - l + 1;
        int n2 = r - m;
 
        /* Create temp arrays */
        int L[] = new int[n1];
        int R[] = new int[n2];
 
        /*Copy data to temp arrays*/
        for (int i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (int j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];
 
        /* Merge the temp arrays */
 
        // Initial indexes of first and second subarrays
        int i = 0, j = 0;
 
        // Initial index of merged subarray array
        int k = l;
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            }
            else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }
 
        /* Copy remaining elements of L[] if any */
        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }
 
        /* Copy remaining elements of R[] if any */
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }
 
    // Main function that sorts arr[l..r] using
    // merge()
    void sort(int arr[], int l, int r)
    {
        if (l < r) {
            // Find the middle point
            int m = l + (r - l) / 2;
 
            // Sort first and second halves
            sort(arr, l, m);
            sort(arr, m + 1, r);
 
            // Merge the sorted halves
            merge(arr, l, m, r);
        }
    }
 
    /* A utility function to print array of size n */
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i = 0; i < n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
 
    // Driver code
    public static void main(String args[])
    {
        int arr[] = { 12, 11, 13, 5, 6, 7 };
 
        System.out.println("Given Array");
        printArray(arr);
 
        MergeSort ob = new MergeSort();
        ob.sort(arr, 0, arr.length - 1);
 
        System.out.println("\nSorted array");
        printArray(arr);
    }
}

Phân tích

Trong Merge sort, danh sách đầu vào được chia thành hai phần và chúng được giải theo cách đệ quy. Sau khi giải quyết các vấn đề phụ, chúng được hợp nhất bằng cách quét kết quả của các vấn đề phụ . Giả sử T(n) là độ phức tạp của sắp xếp Hợp nhất với n phần tử. Sự lặp lại cho Sắp xếp hợp nhất có thể được định nghĩa là:

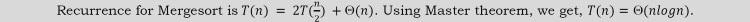
Về Master Theorem của thuật toán Chia để trị các bạn có thể xem lại ở bài viết này

Performance

10.10 Heap Sort

Heapsort là một thuật toán sắp xếp dựa trên so sánh và là một phần của selection sort. Mặc dù trong thực tế trên hầu hết các máy tính khi áp dụng thuật toán này chậm hơn so với việc triển khai tốt Quick sort, nhưng nó có lợi thế là thời gian chạy Θ(nlogn) trong trường hợp xấu nhất thuận lợi hơn. Heapsort là một thuật toán tại chỗ nhưng không phải là một sắp xếp ổn định.

Performance

Thuật toán này mình đã trình bày trong phần ứng dụng của Heap, các bạn có thể xem lại ở đây hoặc tham khảo thêm ở đây