Chương 1: Introduction - 5. Ứng dụng trong phân tích thuật toán

Từ cuộc thảo luận trong bài viết trước (cho cả ba ký hiệu: worst case, best case, và average case), chúng ta đã hiểu được rằng trong mọi trường hợp với một hàm f(n), chúng ta cố gắng tìm 1 hàm g(n) xấp xỉ với hàm f(n) với n là các giá trị lớn(qua ngưỡng n0).
Điều này có nghĩa là g(n) là 1 đường cong xấp xỉ f(n) với n là các giá trị lớn(qua ngưỡng n0) như trong các hình ảnh đồ thị ở bài viết trước.
Trong toán học, chúng ta gọi một đường cong như thế là asymptotic analysis - đường cong tiệm cận
=> Vì lý do này, chúng ta gọi phân tích thuật toán là asymptotic analysis-phân tích tiệm cận

1.19 Hướng dẫn Asymptotic Analysis

Có một số quy tắc chung giúp chúng ta xác định được thời gian chạy của một thuật toán\

1. Loops: Thời gian chạy của một vòng lặp tối đa là thời gian chạy của các câu lệnh bên trong vòng lặp (bao gồm cả các bài kiểm tra) nhân với số lần lặp.

//executes n times
for(i=1; i<=n; i++)
    m = m + 2;  //constant time, c

Total time = 1 hằng số c * n lần lặp = c*n = O(n)\

2. Nested loops: Phân tích từ trong ra ngoài. Tổng thời gian chạy là tích của kích thước tất cả các vòng lặp.

//outer loop executed n times
for(i=1; i<=n; i++){
    //inner loop executed n times
    for(j=1; j<=n; j++)
        k = k + 1; //constant time
}

Total time = c * n * n = c * n^2 = O(n^2)

3. Consecutive statements - Các câu lệnh liên tiếp: Thêm độ phức tạp về thời gian của mỗi câu lệnh.

x = x + 1; //constant time
for(i=1; i<=n; i++)
    m = m + 2;  //constant time, c
    
//outer loop executed n times
for(i=1; i<=n; i++){
    //inner loop executed n times
    for(j=1; j<=n; j++)
        k = k + 1; //constant time
}

Total time = c0 + c1 * n + c2 * n^2 = O(n^2)

4. If-then-else statements: Tính thời gian chạy trong trường hợp Worst case, chạy câu lệnh kiểm tra trong điều kiện if, sau đó chạy tiếp trong body của if hoặc else (Tùy theo khối lượng tính toán của phần nào lớn hơn)

//constant c0
if(length() == 0){
    return false; //constant c1
}
else{ //(constant + constant) * n
    for(int i = 1; i <= n; i++){
        if(list[i].equals(otherList.list[i] == false){ //constant c2
            return false; //constant c3
        }
    }
}

Total time = c0 + c1 + (c2+c3) * n = O(n)

5. Logarithmic complexity: Một thuật toán là O (logn) nếu mất một khoảng thời gian không đổi để cắt kích thước bài toán đi một phần nhỏ (thường là ½). Để làm ví dụ, chúng ta hãy xem xét chương trình sau:

for(i=1; i<=n;){
    i = i*2;
}

Nếu chúng ta quan sát kỹ, giá trị của i đang tăng gấp đôi mỗi lần. Ban đầu i = 1, trong bước tiếp theo I = 2 và trong các bước tiếp theo i = 4, 8, v.v.
Giả sử rằng vòng lặp đang thực thi một số lần k. Ở bước thứ k thứ 2^k = n, và ở bước thứ (k + 1), chúng ta ra khỏi vòng lặp.
Lấy logarit cho cả 2 vế của phương trình 2^k = n
=> log(2^k) = log(n
=> k * log2 = log(n)
=> k = log(n) (// Giả sử chúng ta lấy logarit cơ số 2 => log2 = 1)

Tương tự, đối với trường hợp i giảm dần dưới đây, rate of growth trong trường hợp worst case là O (logn).

for(i=n; i>=1;){
    i = i/2;
}

Lưu ý quan trọng:
Khi ta nói về big O-notation, cơ số của hàm log là không quan trọng.
Giống như O (n) có thể có nghĩa là 2n, hoặc 10n hoặc 10^6 * n, tương tự, O(log n) có thể có nghĩa là log(2) n hoặc lo(10) n hoặc log(e) n. Nó không quan trọng.
Điều quan trọng là đối với n đủ lớn, O(logn) <O(n) <O(n.logn) <O(n^2) ~ Nghĩa là ta chỉ quan tâm tới tốc độ biến thiên rate of growth của hàm số.

1.20 Đơn giản hóa các thuộc tính của các ký hiệu tiệm cận

• Transitivity: f(n) = Θ(g(n)) and g(n) = Θ(h(n)) ⇒f(n) = Θ(h(n)). Hợp lệ với cả O và Ω.
• Reflexivity: f(n) = Θ(f(n)). Hợp lệ với cả O và Ω.
• Symmetry: f(n) = Θ(g(n)) khi và chỉ khi g(n) = Θ(f(n)).
• Transpose symmetry: f(n) = O(g(n)) khi và chỉ khi g(n) = Ω(f(n)).
• Nếu f(n) nằm trong O(k * g(n)) với bất kỳ hằng số k > 0, thì f(n) cũng nằm trong O(g(n))
• Nếu f1(n) nằm trong O(g1(n)) và f2(n) nằm trong O(g2(n)) thì f1(n) * f2(n) nằm trong O(g1(n) * g2(n)).

1.21 Các phép tính Logarithms và Summations thường được sử dụng

Đây đều là các phép tính mà ngày xưa chúng ta từng được học nhưng có lẽ ít được sử dụng nên đã quên(Hi vọng các bạn không giống mình) 😂

Logarithms

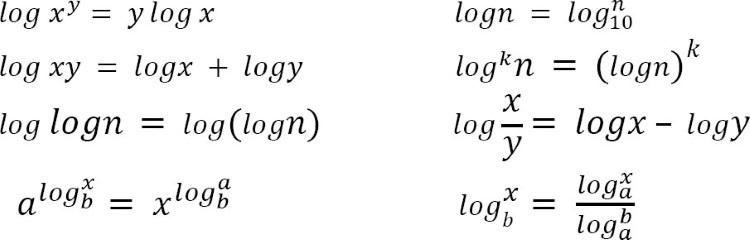
Arithmetic series - Chuỗi số học

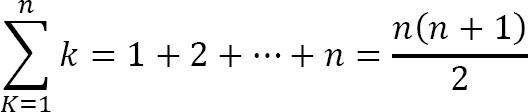
Geometric series

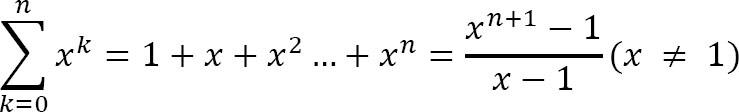
Harmonic series

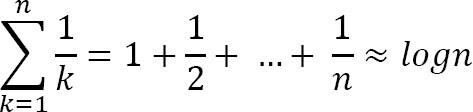
Và 1 vài công thức quan trọng khác

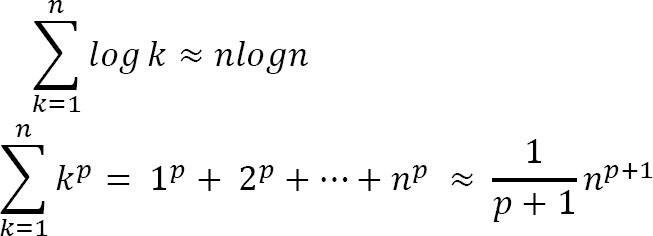
Tạm kết

Ok tới đây thôi, bài viết này hơi nhiều về toán học, hi vọng mọi người sẽ nhớ lại được những kiến thức ngày xưa 😁
Bài sau mình sẽ trình bày cơ bản các định lý chính của giải thuật chia để trị(Divide and Conquer).