Chương 7: PRIORITY QUEUES AND HEAPS - 3.Problems & Solutions(01-13)

Problem-1

Có một min-heap với bảy phần tử riêng biệt sao cho việc duyệt preorder traversal của nó có thể cung cấp cho các phần tử theo thứ tự được sắp xếp không?

Solution: Yes. Đối với cây bên dưới, duyệt preorder traversal tạo ra thứ tự tăng dần.

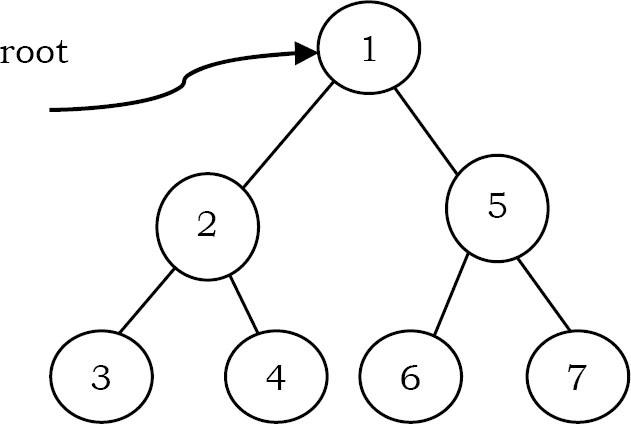
Problem-2

Có một max-heap với bảy phần tử riêng biệt sao cho việc duyệt preorder traversal của nó có thể cung cấp cho các phần tử theo thứ tự được sắp xếp không?

Solution: Yes. Đối với cây bên dưới, duyệt preorder traversal tạo ra thứ tự giảm dần.

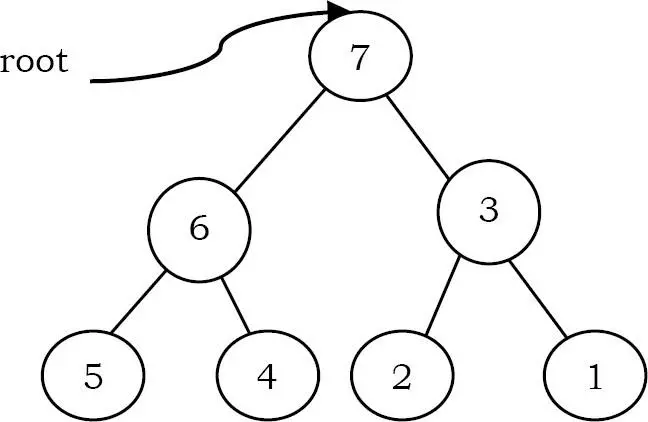
Problem-3

Có một min-heap/max-heap với bảy phần tử riêng biệt để việc duyêt inorder traversal của nó cung cấp cho các phần tử theo thứ tự được sắp xếp không?

Solution: No. Vì heap phải là min-heap hoặc max-heap, gốc sẽ giữ phần tử nhỏ nhất hoặc phần tử lớn nhất. Một phép duyệt inorder traversal sẽ truy cập vào gốc của cây như là bước thứ hai của nó, đây không phải là vị trí thích hợp nếu gốc của cây chứa phần tử nhỏ nhất hoặc lớn nhất.

Problem-4

Có một min-heap/max-heap với bảy phần tử riêng biệt sao cho, quá trình duyệt theo postorder traversal của nó cung cấp cho các phần tử theo thứ tự được sắp xếp không?

Solution: Yes. Có, nếu cây là một max-heap và chúng ta muốn thứ tự giảm dần (bên dưới bên trái) hoặc nếu cây là một min-heap và chúng ta muốn thứ tự tăng dần (bên dưới bên phải).

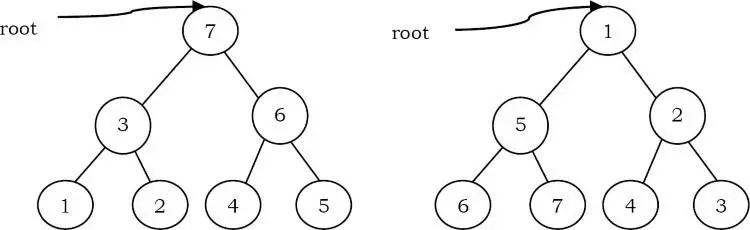
Problem-5

Số lượng phần tử tối thiểu và tối đa trong một heap có chiều cao h là bao nhiêu?

Solution: Vì heap là một cây nhị phân hoàn chỉnh (tất cả các cấp đều chứa các node đầy đủ ngoại trừ có thể là cấp thấp nhất), nên nó có tối đa $2^{h+1} – 1$ phần tử (nếu nó đầy đủ). Điều này là do, để có được các node tối đa, chúng ta cần điền đầy đủ tất cả các mức h và số lượng node tối đa không là gì ngoài tổng của tất cả các node ở tất cả các mức h.

Để có được số node tối thiểu, chúng ta nên điền đầy đủ các mức h – 1 và mức cuối cùng chỉ với một phần tử. Kết quả là số node tối thiểu không là gì ngoài tổng của tất cả các node từ mức h – 1 cộng với 1 (đối với mức cuối cùng) và ta được 2h – 1 + 1 = 2h phần tử (nếu mức thấp nhất chỉ có 1 phần tử và tất cả các cấp độ khác đã hoàn thành).

Problem-6

Chứng minh rằng chiều cao của một heap có n phần tử là logn?

Solution: Một heap là một cây nhị phân hoàn chỉnh. Tất cả các level, ngoại trừ mức thấp nhất, đều đầy đủ. Một heap có ít nhất $2^h$ phần tử và nhiều nhất các phần tử $2^h ≤ n ≤ 2^{h+1} – 1$. Điều này nghĩa là $h ≤ logn ≤ h + 1$. Vì h là số nguyên nên $h = logn$.

Problem-7

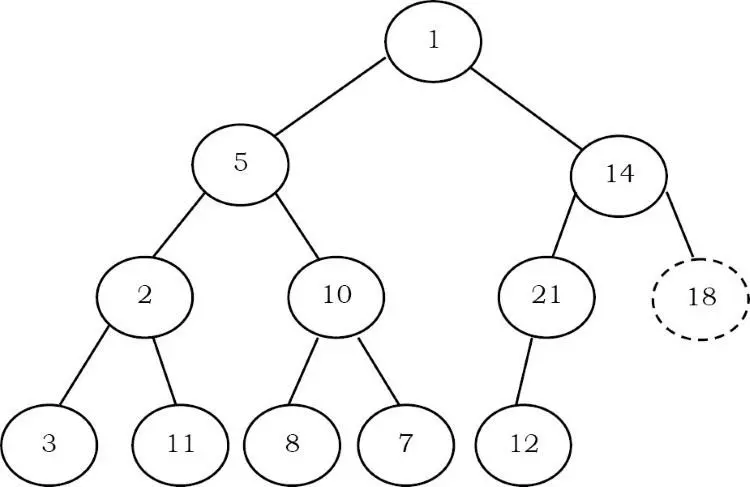
Cho một min-heap, hãy đưa ra thuật toán tìm phần tử lớn nhất.

Solution: Đối với một heap tối thiểu nhất định, phần tử tối đa sẽ luôn chỉ ở lá. Bây giờ, câu hỏi tiếp theo là làm thế nào để tìm các node lá trong cây. Nếu chúng ta quan sát kỹ thì node tiếp theo của phần tử cha cuối cùng chính là node lá đầu tiên. Vì phần tử cuối cùng luôn ở vị trí thứ $h → count – 1$, nên node tiếp theo của cha mẹ nó (cha mẹ tại vị trí $(h → count – 1)/2$) có thể được tính như sau:

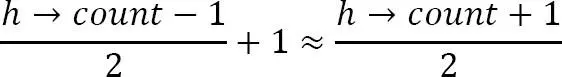
Bây giờ, bước duy nhất còn lại là quét các node lá và tìm node lớn nhất trong số chúng.

    public int FindMaxInMinHeap(Heap h){
        int Max = -1;
        for(int i = (h.count + 1)/2; i < h.count; i++){
            if(h.array[i] > Max){
                Max = h.array[i];
            }
        }
        return Max;
    }

Time Complexity: $O(n/2) ≈ O(n)$

Problem-8

Đưa ra thuật toán xóa một phần tử tùy ý khỏi min heap.

Solution: Để xóa một phần tử, đầu tiên chúng ta cần tìm kiếm phần tử đó. Giả sử rằng chúng ta đang sử dụng phép duyệt level order traversal để tìm phần tử. Sau khi tìm thấy phần tử, chúng ta cần làm theo DeleteMin process.

Time Complexity = Thời gian tìm phần tử + Thời gian xóa phần tử = $O(n) + O(logn) ≈ O(n).$ // Thời gian tìm kiếm chiếm phần lớn.

Problem-9

Đưa ra một thuật toán để xóa phần tử ở vị trí thứ i trong một min-heap.

Solution:

    public int Delete(Heap h, int i){
        int key;
        if(h.count < i){
            System.out.println("Wrong position");
            return -1;
        }
        key = h.array[i];
        h.array[i] = h.array[h.count - 1];
        h.count--;
        h.PercolateDown(i);
        return key;
    }

Time Complexity = O(logn).

Problem-10

Chứng minh rằng, đối với một cây nhị phân đầy đủ có chiều cao h thì tổng chiều cao của tất cả các node là $O(n – h)$.

Solution: Một cây nhị phân đầy đủ có $2i$ node trên một level. Ngoài ra, một node trên level $i$ có độ sâu $i$ và độ cao $h – i$. Chúng ta hãy giả sử rằng S biểu thị tổng chiều cao của tất cả các node này và S có thể được tính như sau:

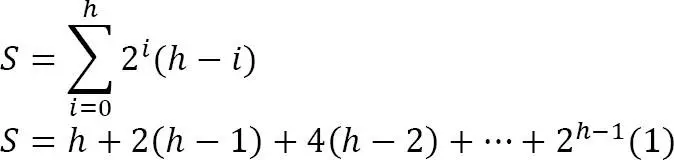
Nhân với 2 ở cả hai vế ta được: $2S = 2h + 4(h – 1) + 8(h – 2) + ··· + 2^h (1)$

Bây giờ, trừ $S$ từ $2S$: $2S – S = –h + 2 + 4 + ·· + 2^h ⇒ S = (2^{h+1} – 1) – (h – 1)$

Nhưng, chúng ta đã biết rằng tổng số node n trong một cây nhị phân hoàn chỉnh có chiều cao h là $n = 2^{h+1} – 1$. Điều này mang lại cho chúng ta: $h = log(n + 1)$.

Cuối cùng, thay $2^{h+1} – 1$ với n, ta được: $S = n – (h – 1) = O(n – logn) = O(n – h)$.

Problem-11

Đưa ra thuật toán tìm tất cả các phần tử nhỏ hơn một giá trị nào đó của k trong một binary heap.

Solution: Bắt đầu từ gốc của heap. Nếu giá trị của gốc nhỏ hơn k thì in giá trị của nó và gọi đệ quy một lần cho con bên trái và một lần cho con bên phải. Nếu giá trị của một node lớn hơn hoặc bằng k thì hàm dừng mà không in giá trị đó. Độ phức tạp của thuật toán này là O(n), trong đó n là tổng số node trong heap. Giới hạn này diễn ra trong trường hợp xấu nhất, khi giá trị của mọi node trong heap sẽ nhỏ hơn k, vì vậy hàm phải gọi từng node của heap.

Problem-12

Đưa ra một thuật toán để hợp nhất hai binary max-heaps. Giả sử rằng kích thước của heap đầu tiên là m và kích thước của heap thứ hai là n.

Solution: Một cách đơn giản để giải quyết vấn đề này là:

• Tạo heap có mảng size $m+n$. Đưa toàn bộ heap 1 vào mảng.
• Thêm heap 2 vào mảng và heapify toàn bộ.
• Vì tổng số phần tử trong mảng mới là m + n, nên mỗi thao tác heapify mất O(log(m + n)).

The complexity: O((m + n)log(m + n)).

Problem-13

Chúng ta có thể cải thiện độ phức tạp của Problem-12 không?

Solution: Thay vì heap hóa tất cả các phần tử của mảng m+n, chúng ta có thể sử dụng kỹ thuật “xây heap bằng một mảng các phần tử (heapifying array)”. Chúng ta có thể bắt đầu với các node không phải lá và heapify chúng lại. Điều này có nghĩa là thay cho bước thứ 3 ở Problem 12 ta sẽ tìm node không phải lá đầu tiên và bắt đầu heapifying từ phần tử đó.

Trong phần lý thuyết, chúng ta đã thấy rằng việc xây dựng một heap có n phần tử có độ phức tạp O(n). Ở bài toán này ta sẽ có Time complexity: $O(m + n)$.