Chương 13: SYMBOL TABLES
Bài đăng này đã không được cập nhật trong 2 năm
13.1 Giới thiệu
Từ khi còn nhỏ, tất cả chúng ta đều đã sử dụng từ điển và nhiều người trong chúng ta có một trình xử lý văn bản (chẳng hạn như Microsoft Word) đi kèm với trình kiểm tra chính tả. Trình kiểm tra chính tả cũng là một từ điển nhưng bị giới hạn về phạm vi. Có nhiều ví dụ thời gian thực cho từ điển và một vài trong số đó là:
- Spell checker(Công cụ kiểm tra chính tả)
- Từ điển dữ liệu trong các ứng dụng quản lý cơ sở dữ liệu
- Symbol tables được sinh ra bởi loaders(trình tải), assemblers, and compilers(trình biên dịch)
- Bảng định tuyến trong các thành phần mạng (tra cứu DNS)
Trong khoa học máy tính, chúng ta thường sử dụng thuật ngữ 'symbol table' thay vì 'dictionary' khi đề cập đến kiểu dữ liệu trừu tượng (ADT).
13.2 Symbol Tables là gì?
Chúng ta có thể định nghĩa Symbol Table là một cấu trúc dữ liệu liên kết một value với một key. Nó hỗ trợ các hoạt động sau:
- Tìm kiếm xem một tên cụ thể có trong bảng hay không
- Lấy các thuộc tính của tên đó
- Sửa đổi các thuộc tính của tên đó
- Chèn một tên mới và các thuộc tính của nó
- Xóa tên và thuộc tính của nó
Chỉ có ba thao tác cơ bản trên Symbol Table: tìm kiếm, chèn và xóa.
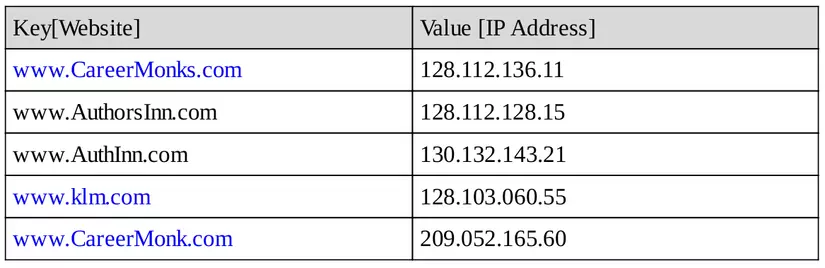
Example: Tra cứu DNS. Giả sử rằng khóa trong trường hợp này là URL và giá trị là địa chỉ IP.
- Chèn URL với địa chỉ IP cụ thể
- URL đã cho, tìm địa chỉ IP tương ứng
13.3 Các triển khai của Symbol Table
Trước khi triển khai các symbol tables, chúng ta hãy liệt kê các cách triển khai có thể được. Symbol tables có thể được thực hiện theo nhiều cách và một số trong số chúng được liệt kê dưới đây.
Unordered Array Implementation
Với phương pháp này, chỉ cần duy trì một mảng là đủ. Nó cần thời gian để tìm kiếm, chèn và xóa trong trường hợp xấu nhất.
Ordered [Sorted] Array Implementation
Trong phần này, chúng ta duy trì một mảng các key và value được sắp xếp.
- Lưu trữ theo thứ tự được sắp xếp theo key
- keys[i] = khóa lớn thứ i
- values[i] = giá trị được liên kết với khóa lớn thứ i
Vì các phần tử được sắp xếp và lưu trữ trong mảng, nên chúng ta có thể sử dụng tìm kiếm nhị phân đơn giản để tìm phần tử. Mất thời gian để tìm kiếm và thời gian để chèn và xóa trong trường hợp xấu nhất.
Unordered Linked List Implementation
Chỉ cần duy trì một Linked List với hai giá trị dữ liệu là đủ cho phương pháp này. Nó cần thời gian để tìm kiếm, chèn và xóa trong trường hợp xấu nhất.
Ordered Linked List Implementation
Trong phương pháp này, trong khi chèn các phím, hãy duy trì thứ tự của các phím trong Linked List. Ngay cả khi danh sách đã được sắp xếp, trong trường hợp xấu nhất, nó cần O(n) thời gian để tìm kiếm, thêm và xóa.
Binary Search Trees Implementation
Các bạn có thể xem lại các bài viết về chương Tree. Ưu điểm của phương pháp này là: không cần nhiều mã và tìm kiếm nhanh [O(logn) on average].
Balanced Binary Search Trees Implementation
Các bạn có thể xem lại các bài viết về chương Tree. Nó là một phần mở rộng của việc triển khai cây tìm kiếm nhị phân và lấy O(logn) trong trường hợp xấu nhất cho các thao tác tìm kiếm, chèn và xóa.
Ternary Search Implementation
Phần này mình sẽ trình bày trong chương String Algorithms. Đây là một trong những phương pháp quan trọng được sử dụng để implementing dictionaries.
Hashing Implementation
Phương pháp này rất quan trọng. Được sử dụng rất nhiều và rộng rãi, mình sẽ trình bày chi tiết ở chương sau: Hashing
13.4 So sáng các loại Implementations của Symbol Table
Chúng ta hãy xem xét bảng so sánh sau đây cho tất cả các triển khai.
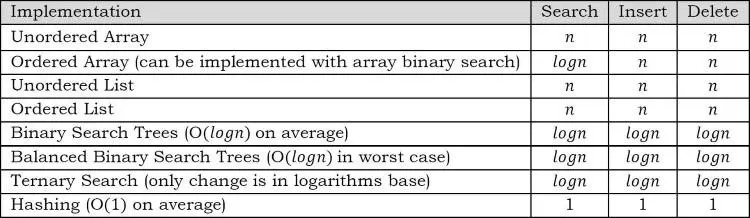
Notes:
- Trong bảng trên, n là kích thước đầu vào.
- Bảng chỉ ra các triển khai có thể được thảo luận chỉ trong cuốn sách này. Nhưng, có thể có những phương pháp triển khai khác.
All rights reserved