2.0K 113 69

Đã đăng vào thg 4 1, 2023 11:29 SA 12 phút đọc

241

Chương 7: PRIORITY QUEUES AND HEAPS - 3.Problems & Solutions(14-25)

Problem-14

Có một thuật toán hiệu quả để hợp nhất 2 max-heaps (được lưu trữ dưới dạng một mảng) không? Giả sử cả hai mảng đều có n phần tử.

Solution: Giải pháp thay thế cho vấn đề merge 2 heap phụ thuộc vào loại của heap. Nếu đó là một heap tiêu chuẩn trong đó mỗi nút có tối đa hai nút con và được lấp đầy sao cho các lá nằm trên tối đa hai hàng khác nhau, thì chúng ta không thể đạt được kết quả tốt hơn O(n) để hợp nhất.

Có một thuật toán O(logm × logn) để hợp nhất hai heap nhị phân có kích thước m và n. Với m = n, thuật toán này có độ phức tạp thời gian $O(log^2n)$ . chúng ta sẽ bỏ qua nó do độ khó và phạm vi của nó. Để có hiệu suất merge tốt hơn, chúng ta có thể sử dụng một biến thể khác của heap nhị phân như FibonacciHeap có thể hợp nhất ở mức trung bình O(1) (đã khấu hao).

Problem-15

Đưa ra thuật toán tìm phần tử nhỏ thứ k trong min-heap.

Solution: Một giải pháp đơn giản cho vấn đề này là: thực hiện xóa k lần từ min-heap.

    public int FindKthLeastElement(Heap h, int k) {
        //Just delete first k-1 elements and return the k-th element
        for (int i = 0; i < k - 1; i++) {
            h.DeleteMin();
        }
        return h.DeleteMin();
    }

Time Complexity: $O(klogn)$ . Vì chúng ta đang thực hiện thao tác xóa k lần và mỗi lần xóa mất O(logn).

Problem-16

Đối với Problem-15, chúng ta có thể cải thiện Time Complexity không?

Solution: Giả sử rằng min-heap ban đầu được gọi là HOrig và min-heap phụ trợ có tên là HAux. Ban đầu, phần tử ở trên cùng của HOrig, phần tử tối thiểu, được chèn vào HAux. Ở đây chúng ta không thực hiện thao tác DeleteMin với HOrig.

Mỗi lần lặp vòng lặp while thứ $i$ cho phần tử nhỏ thứ $i$ và chúng ta cần k vòng lặp để lấy phần tử nhỏ thứ k. Bởi vì kích thước của heap phụ luôn nhỏ hơn k, mỗi lần lặp vòng lặp while, kích thước của heap phụ tăng thêm một và heap ban đầu HOrig không có thao tác nào trong quá trình tìm kiếm, thời gian chạy là $O(klogk)$ .

Trong ảnh là code của tác giả, mình hiểu ý tưởng nhưng thấy có vài điểm sai.

Trong solution viết không thực hiện DeleteMin với HOrig, nhưng ở dòng thứ 5 lại có, sửa thành $HAux.insert(HOrig.array[0]);$ sẽ hợp lý hơn.
Biến heapElement là kiểu int nên trong đoạn else lấy left, right child sẽ lỗi k thể compile được, muốn lấy index của đúng giá trị heapElement trong mảng có lẽ sẽ phải code thêm.

Mình lấy ví dụ, về cơ bản qua mỗi vòng lặp heap phụ sẽ hoạt động như thế này, với k=8 ta được kết quả là 15, k=9 sẽ là 16, ...

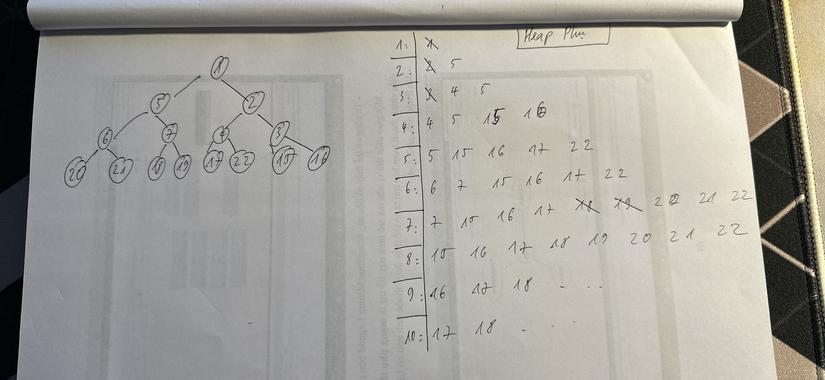
Note: Thuật toán trên hữu ích nếu giá trị k quá nhỏ so với n. Nếu giá trị k xấp xỉ bằng n, thì chúng ta có thể chỉ cần sắp xếp mảng (giả sử sử dụng couting sort hoặc bất kỳ thuật toán sắp xếp tuyến tính nào khác) và trả về phần tử nhỏ thứ k từ mảng đã sắp xếp.

Problem-17

Tìm phần tử max thứ k từ max heap.

Solution: Một giải pháp đơn giản cho vấn đề này là: xây dựng max-heap và thực hiện xóa k lần.

Problem-18

Đối với Problem-17, có giải pháp thay thế nào không?

Solution: Chúng ta có thể sử dụng giải pháp tương tự như Problem-16. Ở vòng lặp cuối cùng, heap phụ chứa phần tử thứ k lớn nhất.

Problem-19

Làm cách nào để triển khai Stack bằng cách sử dụng priority queue sử dụng Heap?

Solution: Để triển khai stack bằng cách sử dụng priority queue PQ (sử dụng min heap), giả sử rằng chúng ta đang sử dụng thêm một biến số nguyên cnt. Stack hoạt động theo nguyên tắc LIFO (vào sau ra trước) và priority queue hoạt động bằng cách gán mức độ ưu tiên cho các phần tử có trong đó. Vì vậy, để triển khai stack bằng priority queue, một biến sẽ được sử dụng để duy trì số lượng mà một phần tử đang được đẩy. Biến này sẽ đóng vai trò là key cho hàng đợi ưu tiên.

Code tham khảo ở đây

import java.util.PriorityQueue;

public class Stack
{

    // cnt is used to keep track of the number of
    //elements in the stack and also serves as key
    //for the priority queue.
    int cnt;
    PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);

    public Stack() {
        cnt = 0;
    }

    public void push(int n) {
        cnt--;
        pq.offer(new int[]{cnt, n});
    }

    public void pop() {
        if (pq.isEmpty()) {
            System.out.println("Nothing to pop!!!");
            return;
        }
        pq.poll();
    }

    public int top() {
        int[] temp = pq.peek();
        return temp[1];
    }

    public boolean isEmpty() {
        return pq.isEmpty();
    }

    public static void main(String[] args) {
        Stack s = new Stack();
        s.push(3);
        s.push(2);
        s.push(1);
        while (!s.isEmpty()) {
            System.out.println(s.top());
            s.pop();
        }
    }
}

Problem-20

Làm cách nào để triển khai Queue bằng cách sử dụng priority queue sử dụng Heap?

Solution: Tương tự problem 19, thay cnt++; trong hàm push.

Problem-21

Cho một tệp lớn chứa hàng tỷ con số, làm cách nào bạn có thể tìm thấy 10 số lớn nhất từ tệp đó?

Solution: Đây là một câu hỏi hay, mình từng gặp câu này khi đi phỏng vấn xin việc. Luôn nhớ rằng khi bạn cần tìm tối đa n phần tử, cấu trúc dữ liệu tốt nhất để sử dụng là priority queues.

Một giải pháp cho vấn đề này là chia dữ liệu thành các bộ gồm 1000 phần tử (giả sử là 1000) và tạo thành một heap, sau đó lấy 10 phần tử từ mỗi heap. Cuối cùng, heapsort tất các bộ gồm 10 phần tử và lấy 10 phần tử hàng đầu trong số đó. Nhưng vấn đề trong cách tiếp cận này là nơi lưu trữ 10 phần tử từ mỗi heap. Điều đó có thể yêu cầu một lượng lớn bộ nhớ vì chúng ta có hàng tỷ số.

Việc sử dụng lại 10 phần tử hàng đầu (từ heap trước đó) trong các khối tiếp theo có thể giải quyết vấn đề này. Nghĩa là lấy khối đầu tiên gồm 1000 phần tử và các khối tiếp theo gồm 990 phần tử mỗi khối. Ban đầu, Heapsort khối đầu tiên gồm 1000 số, lấy tối đa 10 phần tử và trộn chúng với 990 phần tử của khối thứ 2. Một lần nữa, Heapsort 1000 số này (10 từ khối đầu tiên và 990 từ khối thứ 2), lấy 10 phần tử tối đa và trộn chúng với 990 phần tử của tập hợp thứ 3. Lặp lại cho đến tập hợp cuối cùng gồm 990 (hoặc ít hơn) phần tử và lấy tối đa 10 phần tử từ heap cuối cùng. Chúng ta sẽ có 10 phần tử lớn nhất trong file ban đầu.

Time Complexity: $O(n) = n/1000 ×(Heapsort 1000 Elements)$ . Vì độ phức tạp của việc heapsort 1000 phần tử sẽ là một hằng số nên $O(n) = n$ tức là linear complexity(độ phức tạp tuyến tính).

Problem-22

Gộp k list đã sắp xếp có tổng n phần tử: chúng ta được cung cấp k list đã được sắp xếp với tổng số đầu vào n phần tử trong tất cả các list.

Đưa ra thuật toán để hợp nhất chúng thành một danh sách được sắp xếp duy nhất.

Solution: Vì có k danh sách có kích thước bằng nhau với tổng n phần tử nên kích thước của mỗi danh sách là $\frac{n}{k}$ . Một cách đơn giản để giải quyết vấn đề này là:

Lấy danh sách đầu tiên và hợp nhất nó với danh sách thứ hai. Vì kích thước của mỗi danh sách là $\frac{n}{k}$ , bước này tạo ra một danh sách được sắp xếp với kích thước $\frac{n}{k}$ . Điều này tương tự với logic merge sort. Độ phức tạp thời gian của bước này là: $\frac{2n}{k}$ Điều này là do chúng ta cần quét tất cả các phần tử của cả hai danh sách.
Sau đó, hợp nhất đầu ra danh sách thứ hai với danh sách thứ ba. Kết quả là, bước này tạo ra một danh sách được sắp xếp với size $\frac{3n}{k}$ . Độ phức tạp thời gian của bước này là: $\frac{3n}{k}$ . Điều này là do chúng ta cần quét tất cả các thành phần của cả hai danh sách (một có size $\frac{2n}{k}$ và danh sách kia có size $\frac{n}{k}$ ).
Tiếp tục quá trình này cho đến khi tất cả các danh sách được hợp nhất thành một danh sách.

Total time complexity: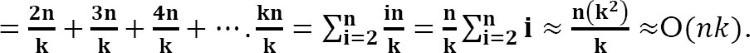

Space Complexity: O(1).

Problem-23

Đối với Problem-22, chúng ta có thể cải thiện độ phức tạp của thời gian không?

Solution:

Chia danh sách thành từng cặp và hợp nhất chúng. Điều đó có nghĩa là, trước tiên hãy lấy hai danh sách cùng lúc và hợp nhất chúng sao cho tất cả các phần tử được phân tách với toàn bộ list là $O(n)$ . Thao tác này đưa ra k/2 cặp các list.
Lặp lại bước 1 cho đến khi số lượng danh sách trở thành một.

Time complexity: Bước 1 thực thi $logk$ lần và mỗi thao tác phân tách tất cả n phần tử trong tất cả các danh sách để tạo danh sách k/2. Ví dụ: nếu chúng ta có 8 danh sách, thì bước đầu tiên sẽ tạo 4 danh sách bằng cách phân tách tất cả n phần tử. Lượt thứ hai sẽ tạo 2 danh sách bằng cách phân tách lại n phần tử và lượt thứ ba sẽ đưa ra 1 danh sách bằng cách phân tách lại n phần tử. Kết quả là tổng thời gian phức tạp là $O(nlogn)$ .

Space Complexity: $O(n)$ .

Problem-24

Đối với Problem-23, chúng ta có thể cải thiện độ phức tạp của thời gian không?

Solution: Hãy để chúng ta sử dụng heap để giảm độ phức tạp của không gian.

Xây dựng max-heap với tất cả các phần tử đầu tiên từ mỗi danh sách trong $O(k)$ .
Trong mỗi bước, trích xuất phần tử tối đa của heap và thêm nó vào cuối Output.
Thêm phần tử tiếp theo từ list của phần tử được trích xuất. Điều đó có nghĩa là chúng ta cần chọn phần tử tiếp theo của danh sách chứa phần tử được trích xuất của bước trước.
Lặp lại bước 2 và bước 3 cho đến khi hoàn thành tất cả các phần tử từ tất cả các danh sách.

Độ phức tạp thời gian = $O(nlogk )$ . Tại một thời điểm, chúng ta có k phần tử max-heap và với tất cả n phần tử, chúng ta chỉ phải đọc heap trong logk thời gian, vì vậy tổng thời gian = $O(nlogk)$ .

Space Complexity: $O(k)$ [for Max-heap].

Problem-25

Cho 2 mảng A và B mỗi mảng có n phần tử. Đưa ra thuật toán tìm n cặp lớn nhất $(A[i], B[j])$ .