7.5 Heaps

Heap là gì?

Một Heap một cây có một số thuộc tính đặc biệt. Yêu cầu cơ bản của heap là giá trị của một node phải > (hoặc <) hơn giá trị của các node con của nó. Đây được gọi là thuộc tính heap. Một heap cũng có thuộc tính bổ sung là tất cả các lá phải ở level h hoặc h – 1 (trong đó h là chiều cao của cây) đối với một số h > 0 (cây nhị phân hoàn chỉnh). Điều đó có nghĩa là đống sẽ tạo thành một cây nhị phân hoàn chỉnh (như hình bên dưới).

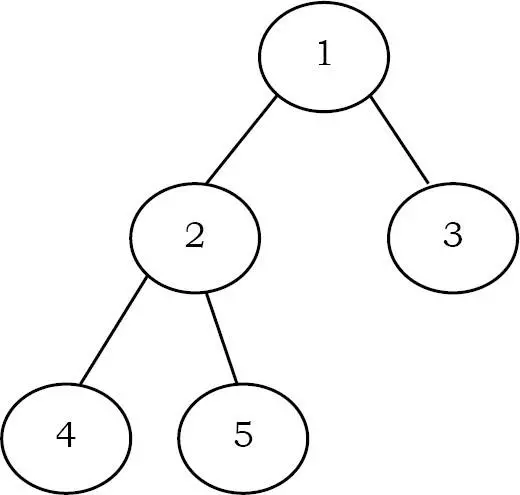
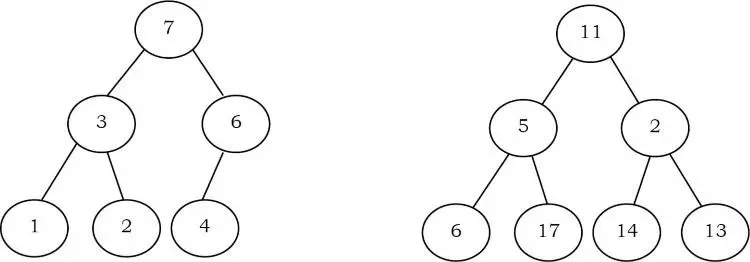
Trong các ví dụ bên dưới, cây bên trái là một heap (mỗi phần tử đều lớn hơn các phần tử con của nó) và cây bên phải không phải là một heap (vì 11 lớn hơn 2).

Các loại Heap

Dựa trên thuộc tính của một heap, chúng ta có thể phân loại heap thành hai loại:

• Min heap: Giá trị của node phải nhỏ hơn hoặc bằng giá trị của node con

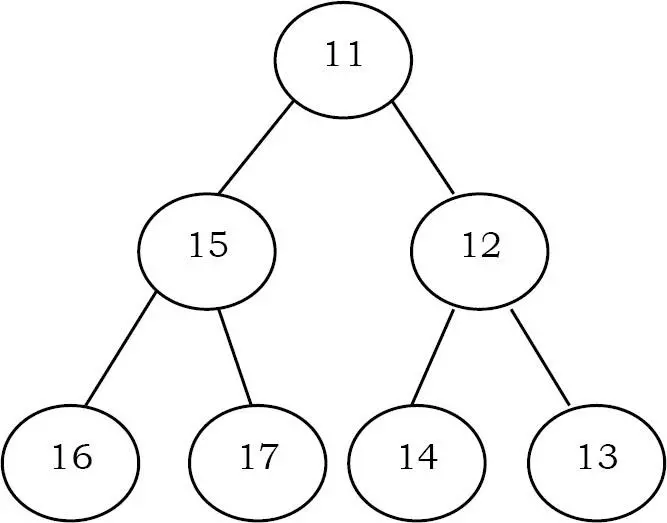
• Max heap: Giá trị của node phải lớn hơn hoặc bằng giá trị của node con

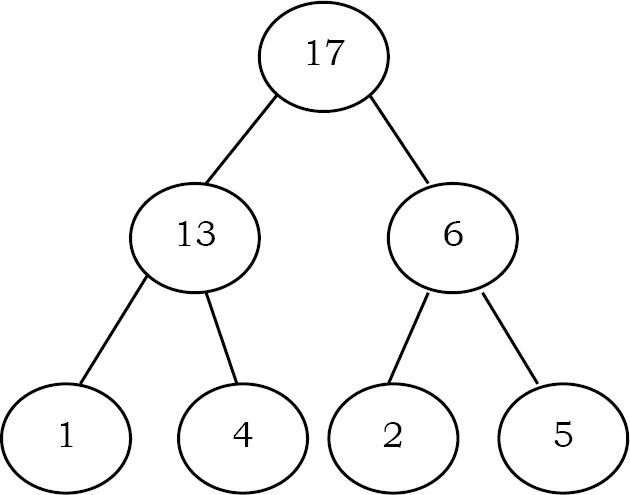
7.6 Binary Heaps

Trong binary heap, mỗi node có thể có tối đa hai node con. Trong thực tế, binary heaps là đủ và chúng ta tập trung vào binary min heaps và binary max heaps cho phần còn lại.

Representing Heaps:

Trước khi xem xét các thao tác trên heap, chúng ta hãy xem các heap có thể được biểu diễn như thế nào. Một khả năng là sử dụng mảng. Vì các đống đang hình thành cây nhị phân hoàn chỉnh nên sẽ không có bất kỳ sự lãng phí vị trí nào. Đối với phần trình bày bên dưới, chúng ta hãy giả sử rằng các phần tử được lưu trữ trong các mảng, bắt đầu từ chỉ mục 0. Max heap trước đó có thể được biểu diễn dưới dạng:

Lưu ý: Đối với phần trình bày còn lại, giả sử rằng chúng ta đang thực hiện các thao tác trong max heap.

Khai báo một Heap

public class Heap {
    public int[] array;
    public int count;                                       //Number of elements in Heap
    public int capacity;                                    //Size of the heap
    public int heap_type;                                   //MinHeap or MaxHeap
    public Heap(int capacity, int heap_type)                {//Refer below sections}
    public int Parent(int i)                                {//Refer below sections}
    public int leftChild(int i)                             {//Refer below sections}
    public int rightChild(int i)                            {//Refer below sections}
    public int getMaximum(int i)                            {//Refer below sections}
}

Note: Giả sử tất cả các chức năng dưới đây là một phần của lớp.

Khởi tạo Heap

    public Heap(int capacity, int heap_type) {
        this.heap_type = heap_type;
        this.count = 0;
        this.capacity = capacity;
        this.array = new int[capacity];
    }

Time Complexity: O(1).

Parent of a Node

Đối với một node ở vị trí thứ i, node cha của nó ở vị trí $\frac { t - 1 } { 2 }$. Trong ví dụ trước, phần tử 6 ở vị trí thứ hai và cha của nó ở vị trí thứ 0.

    public int Parent(int i) {
        if( i <= 0 || i >= this.count){
            return -1;
        }
        return (i-1)/2;
    }

Time Complexity: O(1).

Children of a Node

Tương tự như thảo luận ở trên, đối với một node ở vị trí thứ i, các node con của nó nằm ở vị trí $2*i+1$ và $2*i+2$. Ví dụ, trong cây trên, phần tử 6 ở vị trí thứ hai và các phần tử con 2 và 5 của nó ở vị trí $5(2 * i + l = 2 * 2 + 1)$ và $6(2 * i + 2 = 2 * 2 + 2)$.

    public int leftChild(int i){
        int left = 2*i + 1;
        if(left >= this.count){
            return -1;
        }
        return left;
    }

    public int rightChild(int i){
        int right = 2*i + 2;
        if(right > this.count){
            return -1;
        }
        return right;
    }

Lấy phần tử lớn nhất trong heap

Vì phần tử lớn nhất trong max heap luôn ở gốc nên nó sẽ được lưu trữ tại this.array[0].

public int getMaximum(int i) {
        if(this.count == 0){
            return -1;
        }
        return this.array[0];
    }

Time Complexity: O(1).

Heapifying một phần tử

Sau khi chèn một phần tử vào heap, nó có thể không thỏa mãn các thuộc tính heap. Trong trường hợp đó, chúng ta cần điều chỉnh vị trí của heap để heap hoạt động trở lại. Quá trình này được gọi là heapifying. Trong maxheap, để heapify một phần tử, ta phải tìm cực đại các phần tử con của nó và hoán đổi nó với phần tử hiện tại và tiếp tục quá trình này cho đến khi thuộc tính heap được thỏa mãn tại mọi node.

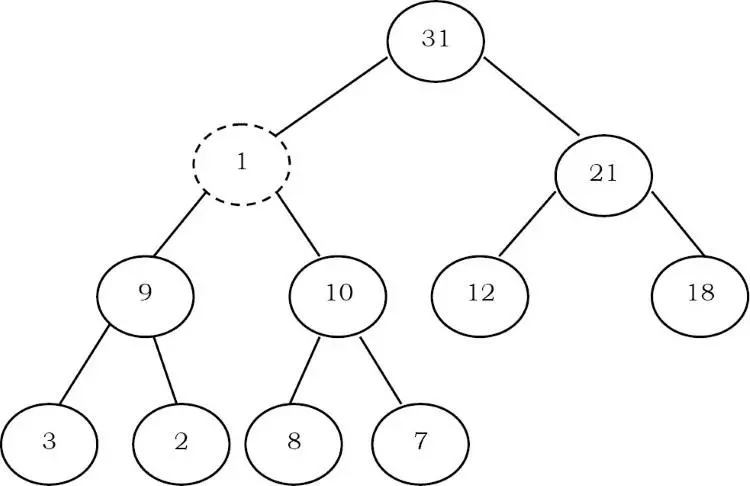
Quan sát: Một thuộc tính quan trọng của heap là, nếu một phần tử không thỏa mãn thuộc tính heap, thì tất cả các phần tử từ phần tử đó đến gốc sẽ gặp vấn đề tương tự. Trong ví dụ bên dưới, phần tử 1 không thỏa mãn thuộc tính heap và phần tử gốc 31 của nó cũng gặp sự cố. Tương tự, nếu chúng ta heapify một phần tử, thì tất cả các phần tử từ phần tử đó đến gốc cũng sẽ tự động thỏa mãn thuộc tính heap. Hãy để chúng ta đi qua một ví dụ. Trong heap trên, phần tử 1 không thỏa mãn thuộc tính heap. Hãy để chúng ta thử làm nặng yếu tố này.

Để heapify 1, hãy tìm node con lớn nhất của nó và hoán đổi với nó.

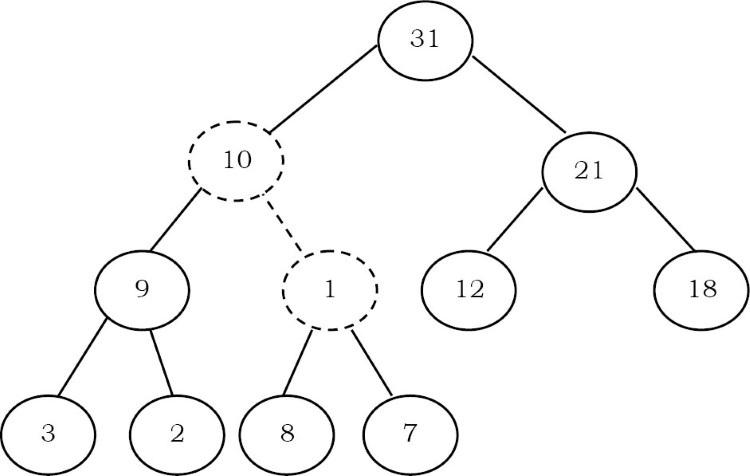
Chúng ta cần tiếp tục quá trình này cho đến khi phần tử thỏa mãn các thuộc tính của heap. Bây giờ, hoán đổi 1 với 8.

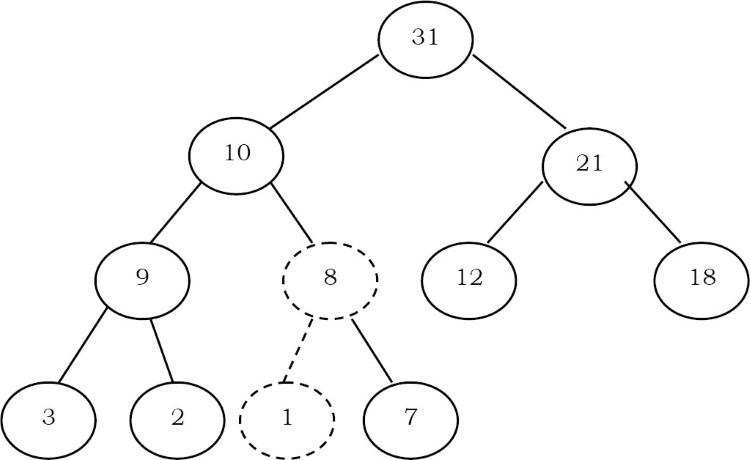
Bây giờ cây thỏa mãn thuộc tính heap. Trong quá trình heapifying ở trên, vì chúng ta đang di chuyển từ trên xuống dưới, quá trình này đôi khi được gọi là percolate down. Tương tự, nếu chúng ta bắt đầu heapifying từ bất kỳ node nào khác đến root, chúng ta có quá trình percolate up khi di chuyển từ dưới lên trên.

    public void PercolateDown(int i){
        int l, r, max, temp;
        l = leftChild(i);
        r = rightChild(i);
        if(l != -1 && this.array[l] > this.array[i]){
            max = l;
        } else {
            max = i;
        }

        if(r != -1 && this.array[r] > this.array[max]){
            max = r;
        }
        if(max != i){
            temp = this.array[i];
            this.array[i] = this.array[max];
            this.array[max] = temp;
            PercolateDown(max);
        }
    }

Time Complexity: O(logn). Heap là một cây nhị phân hoàn chỉnh và trong trường hợp xấu nhất, chúng ta bắt đầu từ gốc và đi xuống lá. Điều này bằng với chiều cao của cây nhị phân hoàn chỉnh. Complexity: O(1).

Xóa một phần tử

Chúng ta chỉ có thể xóa phần tử đó ở gốc. Đây là hoạt động duy nhất được hỗ trợ bởi heap tiêu chuẩn. Sau khi xóa phần tử gốc, hãy sao chép phần tử cuối cùng của heap (cây) và xóa phần tử cuối cùng đó. Sau khi thay thế phần tử cuối cùng, cây có thể không thỏa mãn thuộc tính heap. Để tạo lại heap, hãy gọi hàm PercolateDown.

    int deleteMax(){
        if(this.count == 0){
            return -1;
        }
        int data = this.array[0];
        this.array[0] = this.array[this.count - 1];
        this.count--; //Reducing the heap size
        PercolateDown(0);
        return data;
    }

Thêm một phần tử

Chèn một phần tử tương tự như quá trình heapify và xóa.

• Tăng kích thước heap
• Giữ phần tử mới ở cuối heap (cây)
• Heapify phần tử từ dưới lên trên (root)

Trước khi xem code, chúng ta hãy xem một ví dụ. chúng ta đã chèn phần tử 19 vào cuối heap và điều này không thỏa mãn thuộc tính heap.

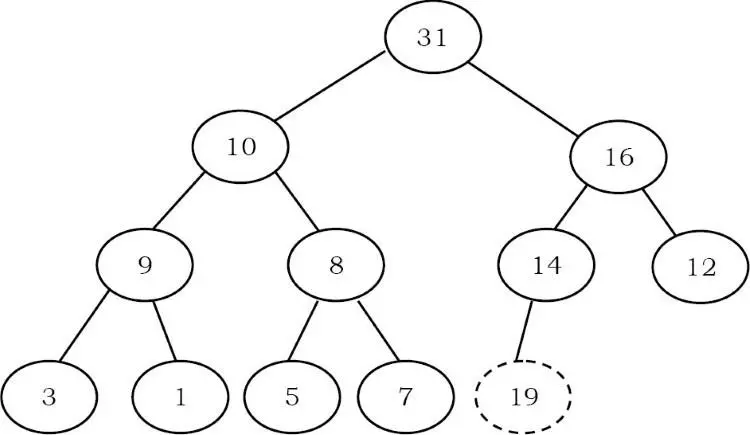
Để heapify phần tử này (19), chúng ta cần so sánh nó với phần tử parent của nó và điều chỉnh chúng. Hoán đổi 19 và 14:

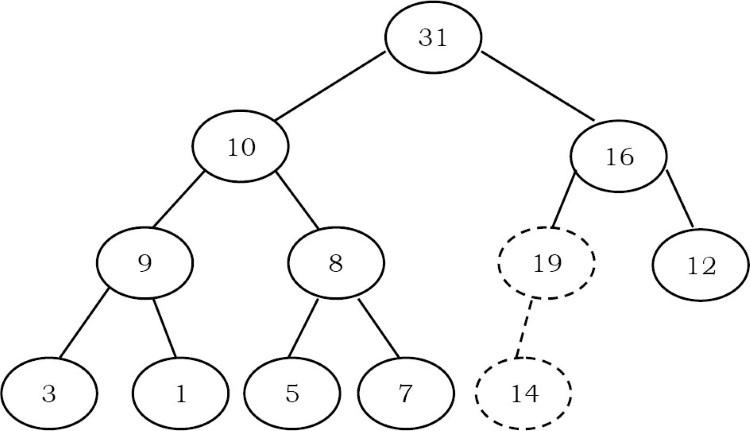
Một lần nữa, hoán đổi 19 và 16:

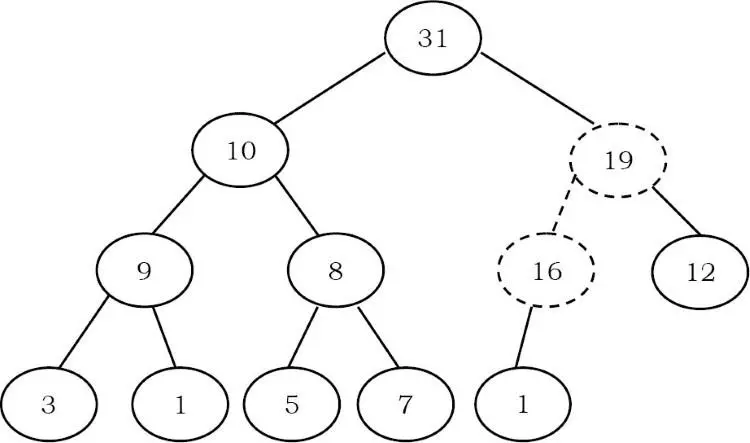
Bây giờ cây thỏa mãn thuộc tính heap. Vì chúng ta đang theo cách tiếp cận từ dưới lên nên đôi khi chúng ta gọi quá trình này là percolate up.

    public void insert(int data){
        int i;
        if(this.count == this.capacity){
            ResizeHeap();
        }
        this.count++;   //increasing the heap size to hold this new item
        i = this.count - 1;
        while(i >= 0 && data > this.array[(i-1)/2]){
            this.array[i] = this.array[(i-1)/2];
            i = (i-1)/2;
        }
        this.array[i] = data;
    }

    public void ResizeHeap(){
        int[] array_old = new int[this.capacity];
        this.array = new int[this.capacity * 2];
        for(int i = 0; i < this.capacity; i++){
            this.array[i] = array_old[i];
        }
        this.capacity *= 2;
        array_old = null;
    }

Xóa Heap

    public void DestroyHeap(){
        this.count = 0;
        this.array = null;
    }

Heapifying the Array

Một cách tiếp cận đơn giản để xây dựng heap là lấy n phần tử đầu vào và đặt chúng vào một heap trống. Điều này có thể được thực hiện với n lần chèn liên tiếp và lấy O(nlogn) trong trường hợp xấu nhất. Điều này là do thực tế là mỗi thao tác chèn mất O(logn).

Để kết thúc bài viết về các binary heaps, chúng ta sẽ xem xét một phương pháp để tạo toàn bộ một đống từ một list data. Phương pháp đầu tiên bạn có thể nghĩ đến có thể giống như sau. Đưa ra một list data, bạn có thể dễ dàng tạo một đống bằng cách chèn từng khóa một. Vì bạn đang bắt đầu với một list từng item, danh sách này được sắp xếp và bạn có thể sử dụng tìm kiếm nhị phân để tìm vị trí phù hợp để chèn khóa tiếp theo với chi phí xấp xỉ O(logn) thao tác.

Tuy nhiên, hãy nhớ rằng việc chèn một mục vào giữa danh sách có thể yêu cầu thao tác O(n) để chuyển phần còn lại của danh sách sang chỗ trống cho mục mới. Do đó, để chèn n khóa vào heap sẽ yêu cầu tổng số thao tác O(nlogn). Tuy nhiên, nếu chúng ta bắt đầu với toàn bộ danh sách thì chúng ta có thể xây dựng toàn bộ đống trong các thao tác O(n).

Quan sát: Các node lá luôn thỏa mãn thuộc tính heap và không cần quan tâm đến chúng. Các node lá luôn ở cuối và để heapify mảng đã cho, chỉ cần chúng ta heapify các node không phải node lá là đủ. Bây giờ chúng ta hãy tập trung vào việc tìm node không phải lá đầu tiên. Phần tử cuối cùng của heap nằm ở vị trí $h → count – 1$, và để tìm node không phải lá đầu tiên, chỉ cần tìm node cha của phần tử cuối cùng là đủ.

    public void BuildHeap(Heap h, int[] A, int n){
        if(h == null){
            return;
        }
        while(n > this.capacity){
            h.ResizeHeap();
        }
        for(int i = 0; i < n; i++){
            h.array[i] = A[i];
        }
        this.count = n;
        for(int i = (n-1)/2; i >= 0; i--){
            h.PercolateDown(i);
        }
    }

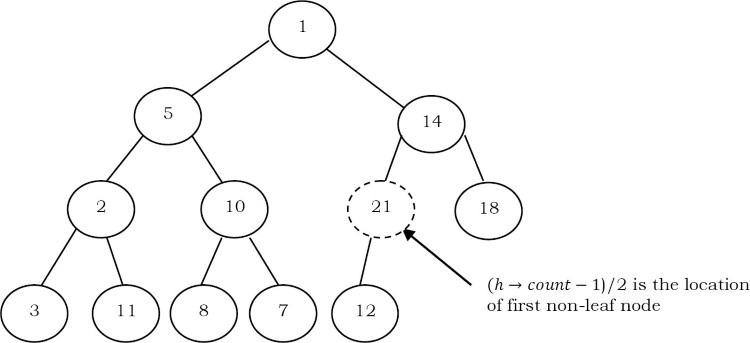
Time Complexity: Giới hạn thời gian tuyến tính của xây dựng heap có thể được hiển thị bằng cách tính tổng chiều cao của tất cả các node. Đối với cây nhị phân hoàn chỉnh có chiều cao h chứa $n = 2^{h+1} – 1$ node, tổng chiều cao của các node là $n – h – 1 = n – logn – 1$ (Chứng minh mình sẽ trình bày trong Problem & Solution). Điều đó có nghĩa là, việc xây dựng heap có thể được thực hiện trong thời gian tuyến tính (O(n)) bằng cách áp dụng hàm PercolateDown cho các node theo thứ tự level ngược lại.

Heapsort

Một ứng dụng chính của heap ADT là sắp xếp (heap sort). Thuật toán sắp xếp heap chèn tất cả các phần tử (từ một mảng chưa được sắp xếp) vào một heap, sau đó loại bỏ chúng khỏi gốc của heap cho đến khi heap trống. Lưu ý rằng sắp xếp heap có thể được thực hiện tại chỗ với mảng được sắp xếp. Thay vì xóa một phần tử, hãy trao đổi phần tử đầu tiên (tối đa) với phần tử cuối cùng và giảm kích thước heap (kích thước mảng). Sau đó, chúng ta heapify phần tử đầu tiên. Tiếp tục quá trình này cho đến khi số phần tử còn lại là một.

    public void HeapSort(int[] A, int n){
        Heap h = new Heap(n, 0);
        int old_size, i, temp;
        BuildHeap(h, A, n);
        old_size = h.count;
        for(i = n - 1; i > 0; i--){ //h.array[0] is the largest element
            temp = h.array[0];
            h.array[0] = h.array[h.count - 1];
            h.array[h.count - 1] = temp;
            h.count--;
            h.PercolateDown(0);
        }
        h.count = old_size;
    }

Time complexity: Khi chúng ta xóa các phần tử khỏi heap, các giá trị sẽ được sắp xếp (vì các phần tử tối đa luôn chỉ là gốc). Vì độ phức tạp thời gian của cả thuật toán chèn và thuật toán xóa là O(logn) (trong đó n là số phần tử trong heap), nên độ phức tạp thời gian của thuật toán sắp xếp heap là O(nlogn).