Feature Engineering (Phần 2): Feature engineering với dữ liệu dạng số liên tục (Continuous Numeric Data)
Bài đăng này đã không được cập nhật trong 6 năm
Xin chào mọi người, trong phần đầu của series này mình đã giới thiệu với mọi người cơ bản về feature engineering bao gồm: vai trò, chức năng và đặc trưng của dữ liệu... Trong phần tiếp theo này chúng ta sẽ tiếp tục với series Understanding Feature Engineering của Dipanjan (DJ) Sarkar để tìm hiểu về một số phương pháp feature engineering với dữ liệu dạng số liên tục (Continuous Numeric Data).
Feature Engineering on Numeric Data
- Dữ liệu số (numeric data) thường biểu thị dữ liệu dưới dạng giá trị vô hướng mô tả các quan sát, bản ghi hoặc thang đo. Ở đây, với từ numeric data chúng ta cần hiểu là dữ liệu liên tục mà không phải dạng dữ liệu rời rạc thường được coi như dạng dữ liệu phân loại (categorical data).
- Dữ liệu số cũng có thể được biểu diễn dưới dạng vectơ của các giá trị, trong đó mỗi giá trị hoặc entity trong vectơ có thể biển diễn cho một đặc trưng cụ thể. Intergers và Floats là các loại dữ liệu số phổ biến nhất và thường được sử dụng cho dạng dữ liệu số liên tục.
- Mặc dù dữ liệu số là dạng dữ liệu có thể đưa trực tiếp vào các mô hình học máy. Tuy nhiên, việc thiết kế các tính năng có liên quan đến kịch bản, vấn đề cần giải quyết và domain của bài toán vẫn là rất cần thiết. Và sau đây, chúng ta sẽ sử dụng python để xây dựng một số phương pháp feature engineering với dữ liệu dạng số liên tục. Đầu tiên, mọi người có thể cài đặt và sử dụng Jupyter notebook để thực hành code.
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as spstats
%matplotlib inline
Xử lý thô (Raw Measures)
Như đã đề cập ở trên, dữ liệu thô có thể được đưa trực tiếp vào các mô hình học máy tùy thuộc vào hoàn cảnh và dạng của dữ liệu. Xử lý thô thường là cách sử dụng biến số trực tiếp của các đặc trưng mà không có bất kỳ hình thức, kỹ thuật biến đổi nào. Thông thường, các biến số này sẽ cho biết giá trị hoặc số lượng của đặc trưng. Chúng ta cùng xem xét Pokémon dataset được cung cấp bởi Kaggle để hiểu rõ hơn.
poke_df = pd.read_csv('datasets/Pokemon.csv', encoding='utf-8')
poke_df.head()
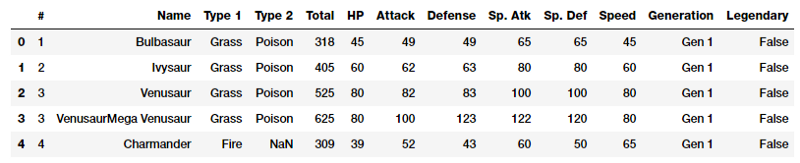
Pokémon là một thương hiệu truyền thông khổng lồ xung quanh có nhân vật hư cấu được gọi là Pokémon. Tóm lại chúng là những con vật hư cấu với siêu năng lực! Bộ dữ liệu này bao gồm các ký tự và số liệu thống kê khác nhau cho mỗi nhân vật.
Xử lý giá trị (Values)
Hãy quan sát hình trên, bạn có thể thấy rằng một số đặc trưng có thể sử dụng trực tiếp bằng giá trị thô. Đoạn code dưới đây sẽ thể hiện rõ hơn những đặc trưng này.
poke_df[['HP', 'Attack', 'Defense']].head()
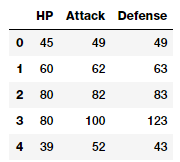
Bảng trên thể hiện đặc trưng với các giá trị số liên tục của nó. Do đó, bạn có thể trực tiếp đưa các đặc trưng này vào thuật toán học máy. Chúng bao gồm từng chỉ số của Pokémon: lượng máu (HP), sức tấn công (Attack), sức phòng thủ (Defense). Trên thực tế, chúng ta hoàn toán có thể sử dụng một số phương pháp thống kê cơ bản cho các đặc trưng này.
poke_df[['HP', 'Attack', 'Defense']].describe()
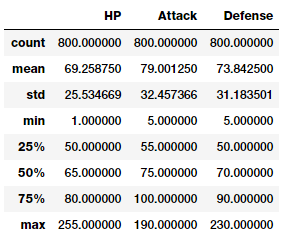
Trên đây là một số mô tả cơ bản về các đặc trưng có dữ liệu dạng số. Chúng ta có thể thấy được số lượng, trung bình, độ lệch chuẩn của dữ liệu của mỗi đặc trưng.
Xử lý số lượng (Counts)
Một dạng khác của xử lý thô (raw measures) bao gồm các đặc trưng thể hiện tần số, số lượng, hoặc sự xuất hiện của các thuộc tính cụ thể. Chúng ta cùng xem xét bộ dữ liệu millionsong dataset trong đó mô tả số lượng hoặc tần xuất các bài hát đã được nghe bởi nhiều người khác nhau
popsong_df = pd.read_csv('datasets/song_views.csv', encoding='utf-8')
popsong_df.head(10)
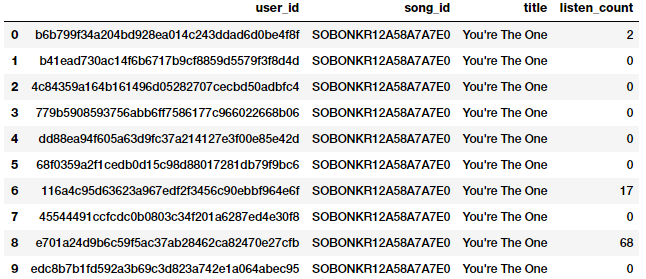
Như hình trên, chúng ta có thể thấy khá rõ ràng trường listen_count có thể sử dụng trực tiếp như một đặc trưng thể hiện tần số, số lượng.
Xử lý nhị phân (Binarization)
Tuy nhiên, trong nhiều bài toán thì tần số, số lượng không liên quan đến vấn đề cần giải quyết. Ví dụ như chúng ta xây dựng một hệ thống đề xuất bài hát, mình chỉ muốn biết liệu một người có quan tâm hay đã nghe một bài hát cụ thể nào đó. Điều này không cần đến số lần bài hát đó đã được nghe vì chúng ta cần quan tâm nhiều hơn đến tất cả các bài hát mà người đó đã nghe. Trong trường hợp này, một phương pháp nhị phân thường được sử dụng. Chúng ta có thể tạo thêm đặc trưng thể hiện việc đã nghe hay chưa từ trường listen_count như sau:
watched = np.array(popsong_df['listen_count'])
watched[watched >= 1] = 1
popsong_df['watched'] = watched
Mọi người cũng có thể sử dụng thư viện Binarizer của scikit-learn
from sklearn.preprocessing import Binarizer
bn = Binarizer(threshold=0.9)
pd_watched = bn.transform([popsong_df['listen_count']])[0]
popsong_df['pd_watched'] = pd_watched
popsong_df.head(11)
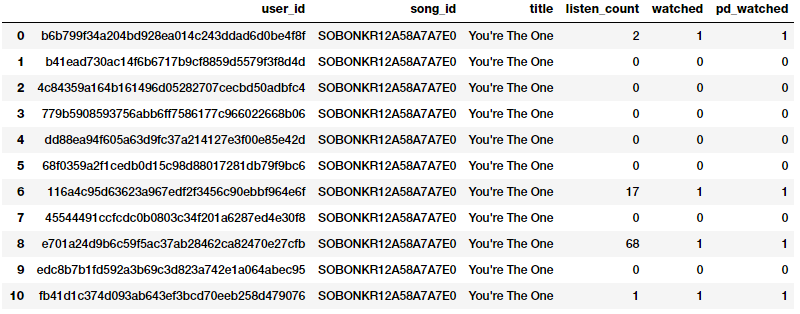
Như hình trên chúng ta có thể thấy rõ rằng cả hai phương pháp đã tạo ra cùng một kết quả. Tính năng nhị phân đã cho biết rằng một bài hát có được nghe hay không bởi mỗi người dùng và có thể đưa vào sử dụng trong các mô hình có liên quan.
Xử lý làm tròn (Rounding)
Thông thường khi xử lý các thuộc tính số liên tục như tỉ lệ hoặc tỉ lệ phần trăm chúng ta có thể không cần các giá trị có độ chính xác quá cao. Do đó có thể làm tròn các tỉ lệ này thành các số nguyên. Các giá trị là số nguyên này có thể sử dụng trực tiếp làm giá trị thô hoặc thậm chí là như các đặc trưng phân loại (categorical) dựa trên lớp rời rạc. Chúng ta thử ứng dụng cách xử lý này với bộ dữ liệu mô tả các mặt hàng trong cửa hàng và độ phổ biến của chúng thể hiện bởi tỷ lệ phần trăm.
items_popularity = pd.read_csv('datasets/item_popularity.csv',
encoding='utf-8')
items_popularity['popularity_scale_10'] = np.array(
np.round((items_popularity['pop_percent'] * 10)),
dtype='int')
items_popularity['popularity_scale_100'] = np.array(
np.round((items_popularity['pop_percent'] * 100)),
dtype='int')
items_popularity
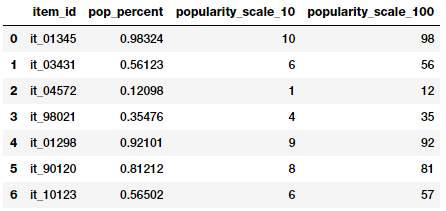
Mình đã sử dụng hai cách làm tròn để có được các thông số như bảng trên. Các đặc trưng mới thể hiện mức độ phổ biến của mặt hàng theo tỉ lệ 1-10 và tỉ lệ 1-100. Và chúng ta có thể sử dụng các giá trị này như là các đặc trưng số học hoặc là đặc trưng phân loại (categorical) tùy thuộc vào vấn đề cần giải quyết.
Xử lý tương tác (Interactions)
Các mô hình học máy có giám sát (supervised learning) thường cố gắng mô hình hóa các đầu ra (các lớp riêng biệt hoặc các giá trị liên tục) như một hàm số của các biến số đặc trưng đầu vào. Ví dụ, một phương trình hồi quy tuyến tính đơn giản có thể được mô tả như sau:
![]()
với các đặc trưng đầu vào được mô tả bởi các biến
![]()
các trọng số hoặc hệ số được thể hiện bởi
![]()
và giá trị dự đoán y. Trong trường hợp này, mô hình tuyến tính đơn giản mô tả mối quan hệ giữa đầu ra và đầu vào hoàn toàn dựa trên các đặc trưng riêng biệt. Tuy nhiên trong thực tế, ta hoàn toàn có thể thử và nắm bắt các tương tác giữa các đặc trưng này. Một mô tả đơn giản về phần mở rộng của công thức hồi quy tuyến tính trên với sự tương tác của các đặc trưng sẽ là:
![]()
và các đặc trưng sẽ được thể hiện bởi
![]()
Mình sẽ thử kỹ thuật xử lý tương tác giữa các đực trưng trên bộ dữ liệu Pokémon:
atk_def = poke_df[['Attack', 'Defense']]
atk_def.head()
Như hình trên chúng ta có thể thấy rằng có hai đặc trưng số liên tục là sức tấn công (Attack) và sức phòng thủ (Defence). Sử dụng scikit-learn chúng ta sẽ xây dựng sự tương tác giữa hai đặc trưng trên.
from sklearn.preprocessing import PolynomialFeatures
pf = PolynomialFeatures(degree=2, interaction_only=False,
include_bias=False)
res = pf.fit_transform(atk_def)
res
Output
------
array([[ 49., 49., 2401., 2401., 2401.],
[ 62., 63., 3844., 3906., 3969.],
[ 82., 83., 6724., 6806., 6889.],
...,
[ 110., 60., 12100., 6600., 3600.],
[ 160., 60., 25600., 9600., 3600.],
[ 110., 120., 12100., 13200., 14400.]])
Ma trận trên bao gồm 5 đặc trưng bao gồm các đặc trưng tương tác mới. Ta có thể có được sự tương tác để tạo ra từng tính năng của như sau:
pd.DataFrame(pf.powers_, columns=['Attack_degree',
'Defense_degree'])
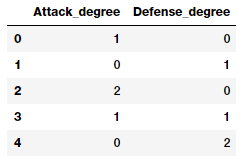
Nhìn vào đầu ra này ta có thể biết được mỗi tính năng thực sự đại diện cho tương tác nào, từ đó ta có thể gán tên cho các đặc trưng. Việc gán tên này chỉ giúp bạn có thể dễ hiểu và dễ truy cập sau này.
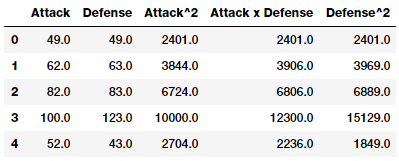
intr_features = pd.DataFrame(res, columns=['Attack', 'Defense',
'Attack^2',
'Attack x Defense',
'Defense^2'])
intr_features.head(5)
Xử lý Binning
Có một vấn đề thường gặp phải với các đặc trưng thô, liên tục là phân phối các giá trị trong các đặc trưng này sẽ bị sai lệch. Điều này được thể hiện ở việc một số giá trị sẽ xuất hiện khá thường xuyên trong khi một số giá trị khác lại khá hiếm. Bên cạnh đó cũng có một vấn đề khác về phạm vi giá trị khác nhau trong các tính năng. Ví dụ, số lượt xem video cụ thể nào đó có thể lớn bất thường (như Despacito chẳng hạn) và một vài video khác rất nhỏ. Sự trực tiếp tính toán trên các đặc trưng này có thể ảnh hưởng xấu đến mô hình của bạn. Do đó, các cách tiếp cận để đối phó với vấn đề này bao gồm xử lý binning và biến đổi (transformations).
Binning, cũng còn có thể được gọi là lượng tử hóa (quantization) được sử dụng để biến đổi các đặc trưng số liên tục thành dạng các đặc trưng phân loại (categorical) riêng biệt. Các giá trị hoặc số rời rạc này có thể được coi là các danh mục hoặc bin. Trong đó, các giác trị số thô, liên tục được đánh dấu hoặc nhóm lại. Mỗi bin đại diện cho một mức độ hoặc cường độ cụ thể và vì vậy, các giá trị số liên tục sẽ thuộc một trong số các bin đó. Các cách tạo bin cụ thể bao gồm tạo bin theo độ rộng cụ thể (fixed-width) và adaptive binning. Chúng ta sẽ sử dụng bộ dữ liệu được trích xuất từ 2016 FreeCodeCamp Developer\Coder survey nói về các thuộc tính khác nhaulieen quan đến lập trình viên và nhà phát triển phần mềm.
fcc_survey_df = pd.read_csv('datasets/fcc_2016_coder_survey_subset.csv',
encoding='utf-8')
fcc_survey_df[['ID.x', 'EmploymentField', 'Age', 'Income']].head()

Biến ID.x về cơ bản là một mã định danh duy nhất cho mỗi lập trình viên hoặc nhà phát triển phần mềm đã thực hiện khảo sát và các trường khác được giải thích khá rõ bởi tên của nó.
Fixed-Width Binning
Như tên gọi của phương pháp này, chúng ta sẽ tạo ra chiều rộng cụ thể cho từng bin việc thiết kế chiều rộng này được xác định trước bởi người phân tích dữ liệu. Mỗi bin có một phạm vi giá trị cố định được gán dựa trên cơ sở một số kiến thức, quy tắc hoặc rằng buộc và phù hợp với yêu cầu chuyên môn của bài toán. Binning dựa trên việc làm tròn giá trị cũng là một trong những cách tiếp cận, trong đó bạn có thể sử dụng thao tác làm tròn như đã thảo luận ở trên. Bây giờ, chúng ta hãy quan sát đặc trưng Age (tuổi) từ bộ dữ liệu khảo sát trên và xem xét phân phối của nó.
fig, ax = plt.subplots()
fcc_survey_df['Age'].hist(color='#A9C5D3', edgecolor='black',
grid=False)
ax.set_title('Developer Age Histogram', fontsize=12)
ax.set_xlabel('Age', fontsize=12)
ax.set_ylabel('Frequency', fontsize=12)
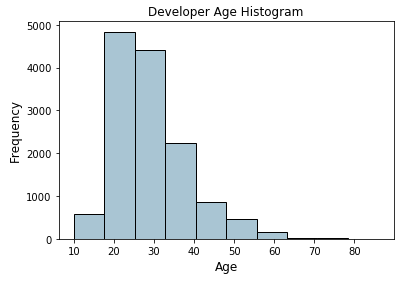
Biểu đồ trên thể hiện phân phối tuổi của các developer và có thể thấy rằng độ tuổi của họ có xu hướng trẻ (lệch về phần ít tuổi hơn). Chúng ta sẽ gán các giá trị thô này vào các bin cụ thể dựa theo sơ đồ sau.
Age Range: Bin
---------------
0 - 9 : 0
10 - 19 : 1
20 - 29 : 2
30 - 39 : 3
40 - 49 : 4
50 - 59 : 5
60 - 69 : 6
... and so on
Và có thể dễ dàng thực hiện điều này bằng cách sử dụng những gì đã thảo luận trong phần làm tròn ở trên. Chúng ta sẽ chia các giá trị thô này cho 10 sau đó làm tròn chúng.
fcc_survey_df['Age_bin_round'] = np.array(np.floor(
np.array(fcc_survey_df['Age']) / 10.))
fcc_survey_df[['ID.x', 'Age', 'Age_bin_round']].iloc[1071:1076]

Như vậy chúng ta sẽ có các bin tương ứng cho từng độ tuổi như sơ đồ trước đó dựa trên phương pháp làm tròn. Nhưng nếu chúng ta cần linh hoạt hơn thì sao? Điều gì xảy ra nếu chúng ta muốn quyết định lại và sửa chữa độ rộng của bin dựa trên quy tắc/logic của riêng mình? Phương pháp Binning dựa trên phạm vi tùy chỉnh sẽ giúp chúng ta thực hiện mục đích này. Mình sẽ xác định lại các bin tuổi của developer theo sơ đồ sau:
Age Range : Bin
---------------
0 - 15 : 1
16 - 30 : 2
31 - 45 : 3
46 - 60 : 4
61 - 75 : 5
75 - 100 : 6
Dựa trên sơ đồ này, bây giờ mình sẽ gán nhãn các thùng cho từng giá trị tuổi của developer và lưu lại giá trị phạm vi của từng bin như các nhãn tương ứng.
bin_ranges = [0, 15, 30, 45, 60, 75, 100]
bin_names = [1, 2, 3, 4, 5, 6]
fcc_survey_df['Age_bin_custom_range'] = pd.cut(
np.array(
fcc_survey_df['Age']),
bins=bin_ranges)
fcc_survey_df['Age_bin_custom_label'] = pd.cut(
np.array(
fcc_survey_df['Age']),
bins=bin_ranges,
labels=bin_names)
# view the binned features
fcc_survey_df[['ID.x', 'Age', 'Age_bin_round',
'Age_bin_custom_range',
'Age_bin_custom_label']].iloc[10a71:1076]
Và kết quả thu được sau quá trình này
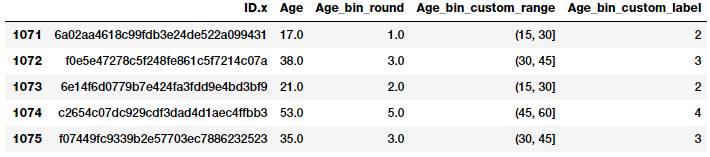
Adaptive Binning
Hạn chế trong việc tạo "bin" có độ rộng cố định là cần phải xác đinh, tạo độ rộng cho các "bin" một cách thủ công. Tuy nhiên, chúng ta có thể kết tạo ra các "bin" không đồng nhất dựa trên số lượng mỗi giá trị ở từng khoảng. Một số "bin" có thể có mật độ cao hơn và một số khác sẽ có mật độ thấp thậm chí là rỗng! Adaptive binning là một phương pháp an toàn trong các kịch bản này. Chúng ta sẽ để dữ liệu tự nói lên đặc trưng của chúng bằng cách sử dụng chính phân phối của dữ liệu để quyết định phạm vi của các "bin".
Binning dựa trên lượng tử hóa (quantile based) lại là một phương pháp tốt thường được sử dụng trong adaptive binning. Quantiles là các giá trị cụ thể hoặc các điểm cắt chia phân phối có giá trị liên tục của một trường thành các phân vùng là các khoảng liền kề rời rạc. Do đó, q-Quantiles sẽ chia một đặc trưng thành q phân vùng bằng nhau. Các ví dụ phổ biến về phương pháp này bao gồm 2-quantiles được gọi là trung vị (median) sẽ chia phân phối thành 2 "bin" bằng nhau, 4-quantiles hay còn gọi là tứ phân chia dữ liệu thành 4 phần bằng nhau và 10-quantiles (decile) tạo ra 10 "bin" có độ rộng bằng nhau. Bây giờ, hay xem phân phối dữ liệu cho trường Income đại diện cho thu nhập của developer.
fig, ax = plt.subplots()
fcc_survey_df['Income'].hist(bins=30, color='#A9C5D3',
edgecolor='black', grid=False)
ax.set_title('Developer Income Histogram', fontsize=12)
ax.set_xlabel('Developer Income', fontsize=12)
ax.set_ylabel('Frequency', fontsize=12)
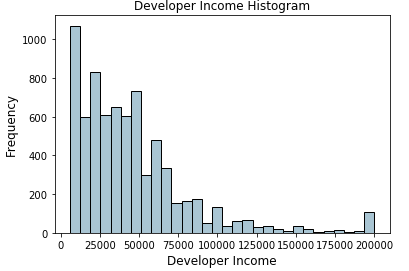
Biểu đồ trên thể hiện phân thối thu nhập của các developer với phân chia 4-quantiles. Đường màu đỏ trong biểu đồ là đường phân chia các bin. Chúng ta sẽ sử dụng các phân chia này để tạo bin dựa trên 4-quantiles.
quantile_labels = ['0-25Q', '25-50Q', '50-75Q', '75-100Q']
fcc_survey_df['Income_quantile_range'] = pd.qcut(
fcc_survey_df['Income'],
q=quantile_list)
fcc_survey_df['Income_quantile_label'] = pd.qcut(
fcc_survey_df['Income'],
q=quantile_list,
labels=quantile_labels)
fcc_survey_df[['ID.x', 'Age', 'Income', 'Income_quantile_range',
'Income_quantile_label']].iloc[4:9]
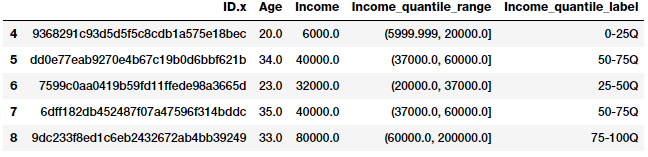
Phương pháp này cho chúng ta một cái nhìn khá rõ ràng về cách hoạt động của adaptive binning. Một điểm quan trọng cần lưu ý ở đây là kết quả của việc tạo bin dẫn đến các đặc trưng phân loại có giá trị riêng biệt và chúng ta có thể cần thêm một bước feature engineering dựa trên đặc trưng phân loại (categorical) để sử dụng nó trong các mô hình học máy. Phương pháp này sẽ được giới thiệu trong phần tiếp theo của series này.
Statistical Transformations
Ở trên chúng ta đã nói về những tác động bất lợi của phân phối dữ liệu không chuẩn đến các mô hình học máy. Bây giờ, chúng ta hãy xem xét một phương pháp khác của feature engineering sử dụng các phép biến đổi thống kê hoặc toán học để giải quyết vấn đề này. Trong phần này, chúng ta sẽ xem xét 2 dạng biến đổi là Log transform và Box-Cox transform. Cả 2 phương pháp biến đổi này đều thuộc họ Power Transform, thường được sử dụng để tạo các phép biến đổi dữ liệu đơn điệu. Ý nghĩa chính của chúng là giúp ổn định phương sai, tuân thủ chặt chẽ phân phối chuẩn và làm cho các dữ liệu độc lập với giá trị trung bình dựa trên phân phối của nó.
Biến đổi Log (Log Transform)
Biến đổi Log thuộc họ power transform. Hàm này có thể được biểu diễn dưới dạng toán học như sau:
![]()
Có thể biểu diễn thành
![]()
Logarit tự nhiên sử dụng b = e trong đó e = 2.71828 thường được gọi là số Euler. Ngoài ra cơ số b = 10 cũng được sử dụng phổ biến trong hệ thống thập phân. Log transform rất hữu ích khi áp dụng cho các phân phối không chuẩn bì chúng có xu hướng mở rộng các giá trị nằm trong phạm vi mật độ thấp và né hoặc giảm các giá trị trong phạm vi mật độ cao. Phương pháp này giúp biến đổi phân phối bị sai lệch trở thành bình thường nhất có thể. Chúng ta tiếp tục sử dụng Log transform với đặc trưng Income ở trên.
fcc_survey_df['Income_log'] = np.log((1+ fcc_survey_df['Income']))
fcc_survey_df[['ID.x', 'Age', 'Income', 'Income_log']].iloc[4:9]
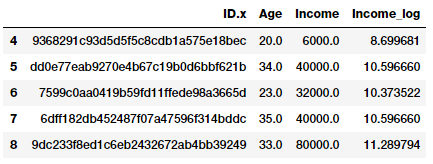
Trường Income_log được tạo ra sau phép biến đổi. Chúng ta hãy xem xét phân phối dữ liệu của đặc trưng này
income_log_mean = np.round(np.mean(fcc_survey_df['Income_log']), 2)
fig, ax = plt.subplots()
fcc_survey_df['Income_log'].hist(bins=30, color='#A9C5D3',
edgecolor='black', grid=False)
plt.axvline(income_log_mean, color='r')
ax.set_title('Developer Income Histogram after Log Transform',
fontsize=12)
ax.set_xlabel('Developer Income (log scale)', fontsize=12)
ax.set_ylabel('Frequency', fontsize=12)
ax.text(11.5, 450, r'$\mu$='+str(income_log_mean), fontsize=10)
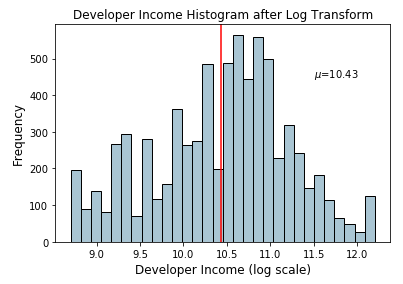
Từ biểu đồ trên chúng ta có thể thấy rõ ràng sau khi biến đối thì giá trị của Income đã tuân theo phân phối chuẩn (Gaussian) hơn so với dữ liệu gốc.
Biến đối Box-Cox (Box-Cox Transform)
Biến đổi Box-Cox là một hàm biến đổi phổ biến khác thuộc họ power transform. Có một điều kiện tiên quyết khi áp dụng phép biến đổi này là các giá trị số được biến đổi phải dương. Trong các trường hợp giá trị âm, có thể shifting bằng cách sử dụng một giá trị không đổi. Về mặt toán học, hàm biến đổi Box-Cox có thể được ký hiệu như sau.
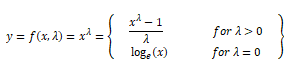
Output y là một hàm của input x và tham số biến đổi λ sao cho khi λ=0 kết quả là một hàm log như đã nói ở trên. Giá trị tối ưu của λ thường được xác định bằng cách sử dụng maximum likelihood hoặc log-likelihood estimation. Bây giờ, chúng ta sẽ thử sử dụng biến đổi Box-Cox với đặc trưng Income của developer như ở trên. Đầu tiên, chúng ta sẽ tìm giá trị λ tối ưu từ phân phối dữ liệu như sau.
income = np.array(fcc_survey_df['Income'])
income_clean = income[~np.isnan(income)]
l, opt_lambda = spstats.boxcox(income_clean)
print('Optimal lambda value:', opt_lambda)
Output
------
Optimal lambda value: 0.117991239456
Sau khi đã có giá trị λ tối ưu sẽ tiếp tục sử dụng biến đổi Box-Cox cho 2 giá trị của λ là λ = 0 và λ = giá trị tối ưu vừa tìm được với dữ liệu Income
fcc_survey_df['Income_boxcox_lambda_0'] = spstats.boxcox(
(1+fcc_survey_df['Income']),
lmbda=0)
fcc_survey_df['Income_boxcox_lambda_opt'] = spstats.boxcox(
fcc_survey_df['Income'],
lmbda=opt_lambda)
fcc_survey_df[['ID.x', 'Age', 'Income', 'Income_log',
'Income_boxcox_lambda_0',
'Income_boxcox_lambda_opt']].iloc[4:9]
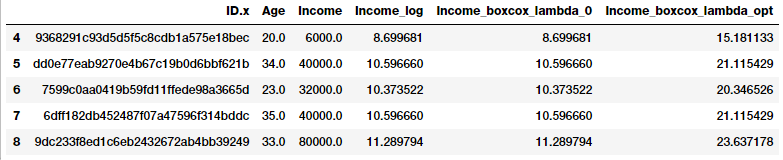
Kết quả thu được phân phối của dữ liệu sau biến đổi Box-Cox đã khá gần với phân phối chuẩn và cũng tương tự biến đổi log ở trên.
Kết luận
Feature engineering luôn vô cùng quan trọng và không thể bỏ qua. Hiện nay, chúng ta có một số phương pháp feature engineering tự động như deep learning hoặc automated machine như framework AutoML (nhưng vẫn nhấn mạnh rằng các phương pháp này vẫn cần các đặc trưng tốt để hoạt động). Thậm chí các phương pháp này đôi khi còn yêu cầu các đặc trưng được thiết kế cụ thể dựa trên loại dữ liệu, domain và vấn đề cần giải quyết.
Như vậy trong bài viết này, chúng ta đã xem xét các cách tiếp cận phổ biến cho dữ liệu dạng số liên tục. Trong phần tiếp theo, chúng ta sẽ tiếp tục xem xét các phương pháp để xử lý dữ liệu phân loại (categorical), rời rạc và các dạng dữ liệu phi cấu trúc trong tương lại.
Tất cả code và dữ liệu được sử dụng trong bài viết các bạn có thể truy cập từ Github của tác giả.
Tài liệu tham khảo
All rights reserved
