Trong phần trước, mình đã giới thiệu về kiểu dữ liệu Graph, cũng như một số định nghĩa liên quan đến kiểu dữ liệu này. Hôm nay mình sẽ đi sâu hơn vào cách sử dụng Machine Learning để giải quyết một số bài toán liên quan đến Graph nhé. Gẹt gô.

1. Tại sao lại cần Machine Learning cho Graph?

Câu hỏi này cũng giống như câu hỏi "Tại sao lại cần Machine Learning (hay Deep Learning)?" nhưng lần này, chúng ta đang xử lý các bài toán với kiểu dữ liệu Graph. Graph mang tính tổng quát hơn so với kiểu dữ liệu Ảnh (Images) hay Text ở chỗ: Ảnh và Text có thể được biểu diễn dưới dạng Graph theo một cấu trúc lưới cố định (ví dụ ta có thể coi mỗi pixel trong ảnh là một node và các node đó được sắp xếp theo một cấu trúc lưới có kích thước $H \times W \times C$). Tuy nhiên, đa phần các graph đều không được "đẹp" như vậy (ví dụ như social graph). Do đó, ngay từ đầu, việc xử lí các bài toán liên quan đến Graph đã là một việc rất chi là "khoai" rồi.

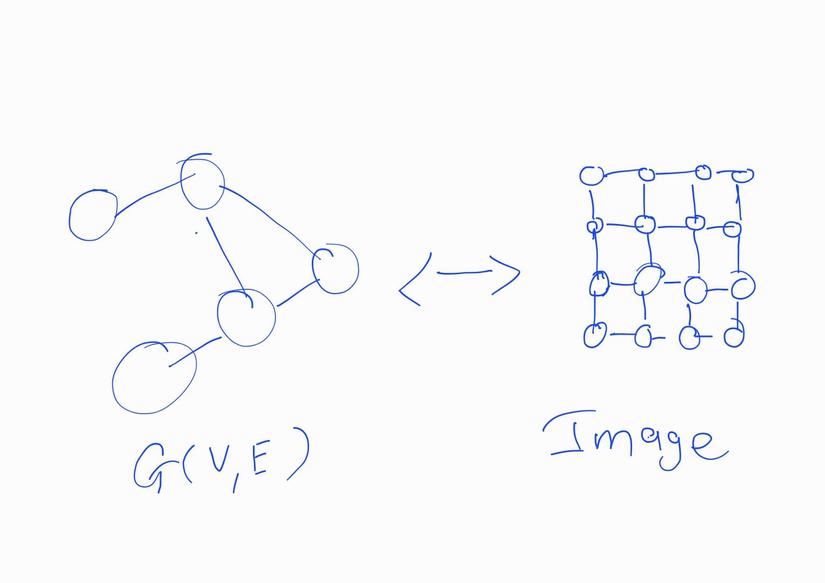
Ngày nay, có rất nhiều ứng dụng có thể được giải quyết bằng cách sử dụng Graph (ví dụ như trong một số lĩnh vực đặc thù như điều chế thuốc chẳng hạn). Tuy nhiên, sự phức tạp đến từ kiểu dữ liệu này (cũng như từng thành phần trong graph) đặt ra nhiều thách thức. Graph ngày nay được cấu thành từ nhiều thành phần có nhiều đặc tính, cũng như có một mối liên hệ nào đó với nhau, gọi là relational graph. Khi đó, việc sử dụng Machine Learning (sâu hơn là Deep Learning) để phân tích các đặc tính này giúp chúng ta đạt được hiệu suất cao khi giải quyết các bài toán phức tạp như trên. Do đó, học Machine Learning đi 🤣

2. Machine Learning with Graphs

Nào, vô món chính của ngày hôm nay nào. Để cho dễ tưởng tượng thì cùng tìm hiểu về Undirected Graph trước nhé. Mà muốn ăn thì phải chuẩn bị nguyên liệu. Để chế biến món "Machine Learning in Graphs" thì cần những nguyên liệu sau:

• Features của graph: vector có d chiều biểu diễn node-features, edge-feature hoặc feature của cả cái graph (nếu làm việc với nhiều graph một lúc).
• Đối tượng hướng tới: node, edge, subset của nodes, một phần hoặc toàn bộ graph.
• Mục tiêu đặt ra: tuỳ vào bài toán cụ thể. 😄

Nào, hãy cùng lướt qua một số ví dụ nhé:

a. Cấp độ Node

Hãy cùng đi qua một số feature khi xét đến node nhé. Đối với feature của node thì ta có thể chia ra làm hai loại chính:

1 . Đặc trưng dựa vào mức độ quan trọng của node (Importance-based features):

Với phương châm "Tui nổi tiếng khi có nhiều người biết đến tui", cách lấy đặc trưng này sẽ dựa vào các node xung quanh node đang muốn lấy đặc trưng, bao gồm số lượng và lượng thông tin của các node đó. Cách lấy đặc trưng này bao gồm 2 phương pháp chính:

• Dựa vào Node-degree $k_v$: Cái này thì mình đã đề cập trong phần 1 rồi, mọi người có thể coi lại qua link này nhé: P1. Tổng quan về Graph
• Dựa vào Node-centrality $c_v$: Có thể hiểu nôm na là: "Tui quan trọng khi những người xung quanh tui cũng quan trọng". Hướng này sẽ lấy đặc trưng của node dựa vào tầm quan trọng của node đang xét. Mà muốn quan trọng thì chính bản thân node đó, cũng như các node xung quanh, đều mang những thông tin có giá trị. Hướng này bao gồm nhiều phương pháp, ở đây mình sẽ chỉ ra một số cái thôi:

i. Betweenness centrality

Ở phương pháp này, chúng ta coi một node là quan trọng khi node này nằm trên nhiều đường đi ngắn nhất (shortest path) giữa các node khác với nhau. Công thức để tìm $c_v$ trong trường hợp này là:

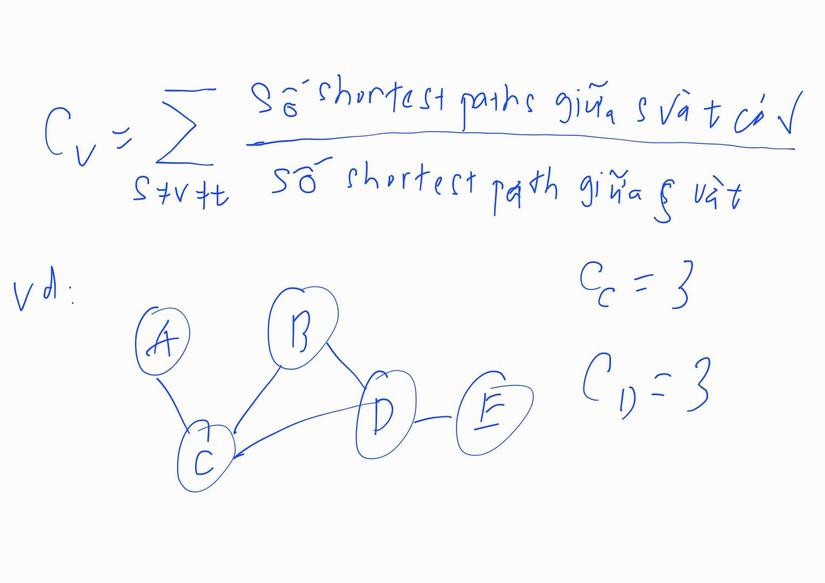
Tại sao $c_c$ lại bằng 3? Ta thấy shortest path từ A đến B là A-C-B, từ A đến D là A-C-D và từ A đến E là A-C-D-E và các shortest path này đều đi qua node C. Ngoài ra, từ B đến D, B đến E và D đến E thì các shortest path giữa các cặp node này đều không đi qua C. Chính vì vậy, dựa theo công thức ở trên, $c_C$ = 3. Tương tự với $c_E$ nhé.

ii. Closeness Centrality

Phương pháp này đúng với tiêu chí: "Nhà càng gần trung tâm thành phố, tiện lợi khi di chuyển đến khắp nơi thì càng được giá". Ở đây, ta coi một node là quan trọng khi node đó nằm trên shortest path tới tất cả các node còn lại. Công thức để tìm $c_v$ trong trường hợp này là:

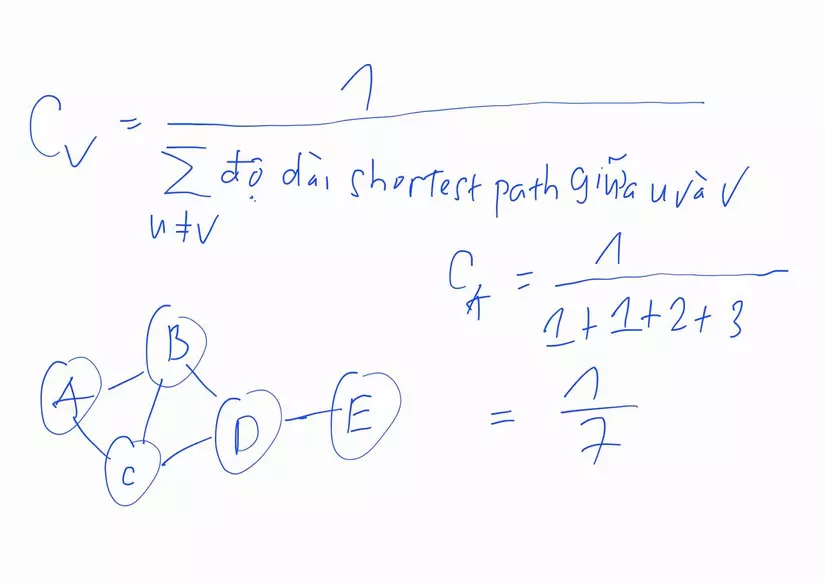
Ta thấy shortest path giữa node A và các node còn lại lần lượt là: A-B, A-C, A-C-D, A-C-D-E. Từ đó ta suy ra được công thức trên.

Nhìn chung, cách lấy đặc trưng dựa vào sự "nổi tiếng" của 1 node được sử dụng khi chúng ta muốn tìm hiểu tầm ảnh hưởng của một node tới các node xung quanh. Cái này thì thường thấy khi làm social graph nè, khi các doanh nghiệp muốn liên hệ với những người nổi tiếng để booking quảng cáo sản phẩm, thì họ sẽ tìm hiểu xem trong 1 social graph ở 1 khu vực nào đó, ai là người có nhiều "kết nối" nhất thì họ sẽ tiếp cận thôi.

2 . Đặc trưng dựa vào cấu trúc hình học (Structure-based features)

Cách lấy đặc trưng này thì lại dựa vào các thuộc tính về cấu trúc của node khi liên kết với các ndoe xung quanh. Cách này thì thường được sử dụng khi chúng ta muốn tìm hiểu vai trò của một node trong một cấu trúc graph. Cũng có nhiều phương pháp khi thực hiện cách lấy đặc trưng này, ví dụ như là Clustering Coefficient, Graphlets, v.v. Trong khuôn khổ bài viết này thì mình sẽ đề cập đến phương pháp Clustering Coefficient nhé, còn Graphlets thì khi đi sâu hơn mình sẽ đề cập kĩ hơn.

Clustering Coefficient $e_v$ của node v là phương pháp dùng để đánh giá tính "kết nối" của các node hàng xóm của node v. Cái lí thuyết này mình nghe giống như kiểu "nhà muốn vững thì móng phải vững", không biết mọi người có thấy thế không. Công thức của cái cách này là:

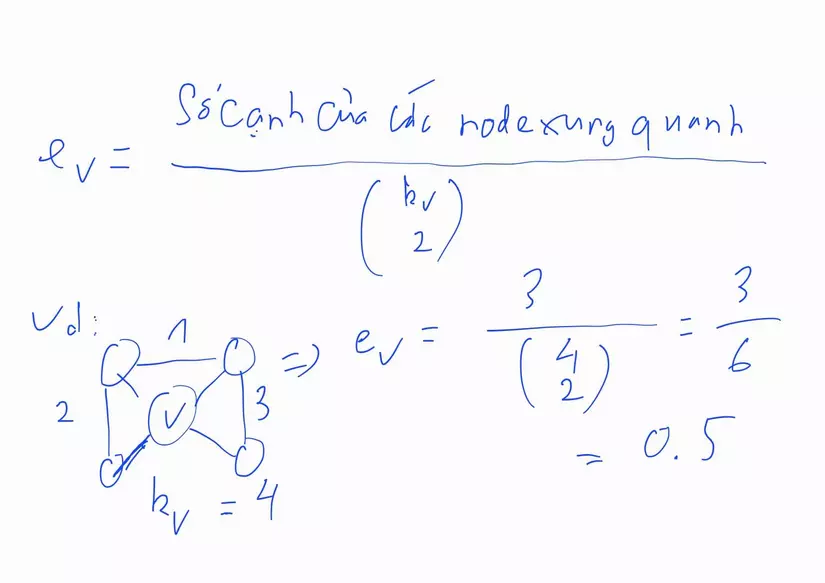
Trong đó tử số là số cạnh nối các node xung quanh node v (không đi qua node v), còn mẫu số là tổ hợp chập 2 của $k_v$ (node-degree của node v). Ví dụ ở trên, ta thấy mẫu số là tổ hợp chập 2 của 4, tử số là 3. Khi đó $e_v$ của node v bằng 0.5.

Mình nghĩ viết đến đây cũng đủ dài và mọi người đọc cũng buồn ngủ rồi 😄 Bài viết này mình đã giới thiệu khái quát về Machine Learning trong Graphs rồi, cũng như một số bài toán ở cấp độ node. Mình sẽ đề cập tiếp trong các bài viết tiếp theo nhé, về cấp độ link và cao hơn là cấp độ graph. Hi vọng mọi người sẽ ủng hộ để mình tiếp tục series này.

Tài liệu tham khảo: CS224W: Machine Learning with Graphs
Link phần 1 nè: P1. Tổng quan về Graph

Update: Mình đã viết xong phần tiếp theo rồi nhé, mọi người có thể đọc tại đây: P4. (Lại là) Machine Learning with Graphs