Đổi gió tí nhỉ, nay thì mình sẽ nói về một mô hình khác của dòng họ Generative models (dòng họ sinh dữ liệu). Các tiền bối đi trước của dòng họ này có thể kể đến là Auto-Encoder, GAN và Flow-based model, đã làm rất tốt vai trò của mình rồi. Nhưng người xưa có câu "Hậu sinh khả uý", thế nên việc con cháu làm tốt hơn các cụ đó là điều đương nhiên rồi. Mô hình đó là Diffusion Model.

Cá nhân mình khi tìm hiểu về dòng dõi Diffusion model thì ban đầu cũng cảm thấy hơi khó hiểu, thế nên mình viết bài này như là một cách tiếp cận dễ thấm hơn cho những bạn nào giống mình. Nào, vô luôn đê.

1. Các tiền bối đã làm tốt, nhưng...

Như mình có đề cập ở phần trên, thì Auto-Encoder (AE), GAN và Flow-based model đều thuộc dòng họ Generative model. Generative model là những model có khả năng sinh dữ liệu nhờ vào việc ánh xạ dữ liệu lên một vùng không gian ẩn nào đó, rồi từ vùng không gian ẩn này thì sẽ sinh ra dữ liệu. Còn nhớ thời các mô hình này mới ra đời thì hai cái "dòng họ" này đã làm mưa làm gió, và đã có rất nhiều paper cũng như ứng dụng được thực hiện. Tuy nhiên thì các model này hiện nay cũng bộc lộ nhiều hạn chế:

• Đối với AE: ý tưởng của AE khá hay khi tối ưu hoá hàm mất mát giữa dữ liệu được sinh ra với đầu vào bằng cách ánh xạ dữ liệu lên một miền không gian ẩn, rồi từ đó khôi phục lại dữ liệu. Tuy nhiên, mô hình lại phụ thuộc vào hàm surrogate loss (một ví dụ của surrogate loss là hinge loss function) Hàm surrogate loss có nhược điểm, đó là nó giống như một cái "hàng rào" phân tách giữa các class dữ liệu với nhau (đấy cũng chính là lí do hàm này thường được sử dụng trong thuật toán SVM) chứ không phải dự đoán liệu dữ liệu sinh ra có cùng phân phối với dữ liệu gốc không.
• Đối với GAN: đây là một mô hình xịn tại thời điểm nó ra mắt. Tuy nhiên vì phải phụ thuộc vào tầng Discriminator trong việc "kiểm tra" dữ liệu (mà thực tế thì thường tầng này là 1 pre-trained model) nên GAN sẽ không có tính "sáng tạo" (không có tính phong phú) trong việc sinh dữ liệu mới. Thêm vào đó, nếu như mạng GAN có kiến trúc quá lớn thì khi huấn luyện sẽ dễ gặp hiện tượng vanishing gradients khiến cho việc sinh dữ liệu trở nên kém hiệu quả hơn. Với lại, thực ra GAN sử dụng một input nhiễu làm đầu vào, rồi từ input nhiễu đó sinh ra data, chứ không phải tìm ra một probability distribution của data đó.
• Đối với Flow-based model: Đây là một model sử dụng phương pháp Normalizing Flows để sinh dữ liệu, bằng cách học Hàm mật độ xác suất (PDF) của input thông qua nhiều quá trình biến đổi. Tuy vậy thì đó cũng chính là điểm yếu của model này khi các layer của mô hình này phải có khả năng invertible (tạm dịch là nghịch đảo) thì mới sinh dữ liệu được (như trong hình dưới thì hàm được dùng ở tầng encoder phải có khả năng invertible thì mới áp dụng vô decoder được).

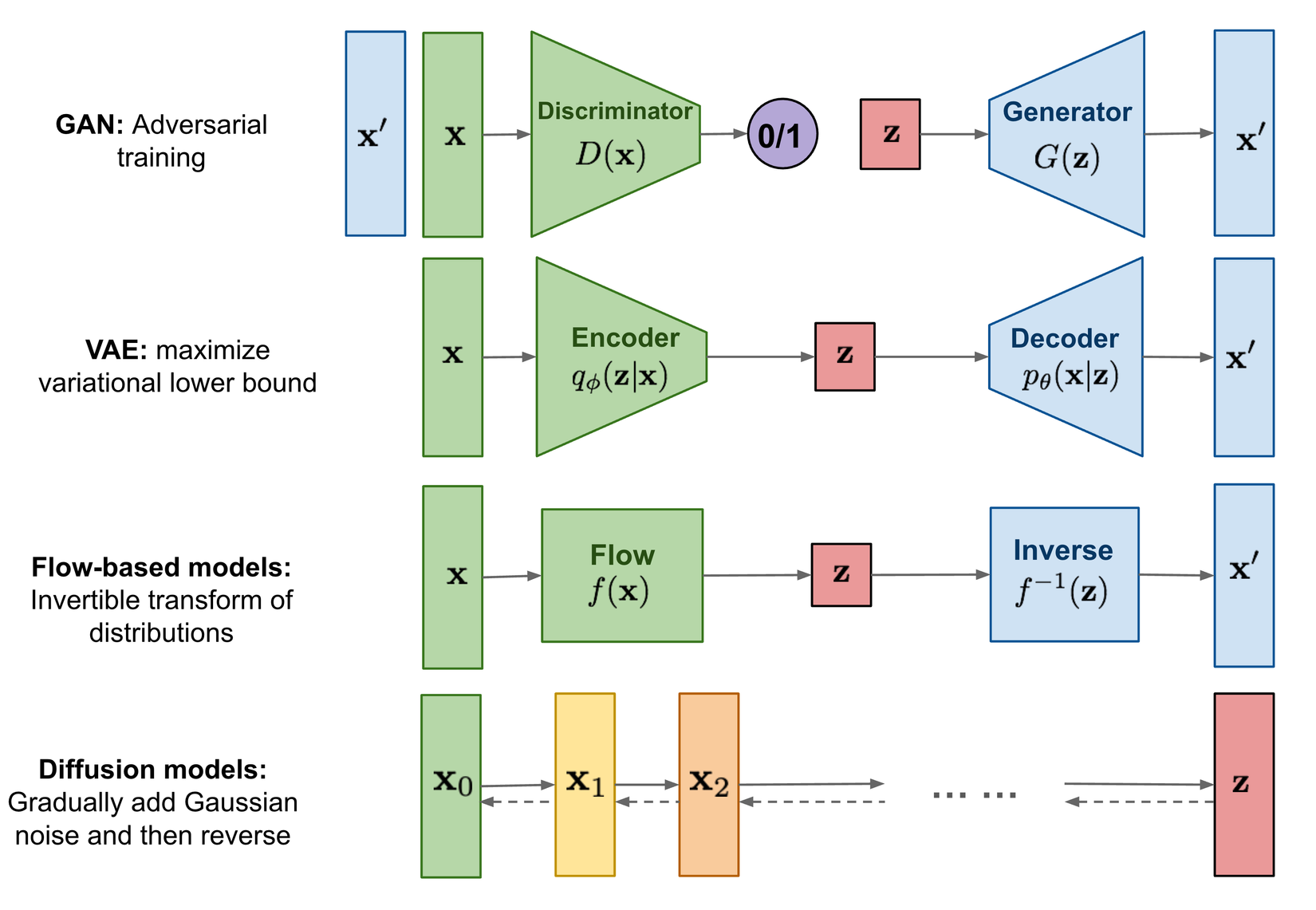
Từ đó, một hậu duệ đã ra đời...

2. Diffusion model vỡ lòng

Mình có một đứa em họ nhưng còn bé xíu, và dĩ nhiên thì lâu lâu mình phải làm nhiệm vụ trông trẻ rồi. Thỉnh thoảng mình có hay mua đồ chơi cho bé. Có một trò chơi mà mình thấy khá là giống với cách mà Diffusion vận hành, đó là cái tranh dán keo mà muốn tô màu cho nó thì phải rắc kim tuyến lên. Cũng chẳng biết phải gọi tên trò chơi đó là gì, tạm gọi là tranh kim tuyến đi. Cái hình ở dưới sẽ minh hoạ cho cái tranh đó.

Về căn bản thì Diffusion model cũng sẽ hoạt động như cách mình tô tranh này vậy đó (dĩ nhiên là không giống 100% rồi, nhưng để minh hoạ cơ chế hoạt động thì cái ví dụ này mình thấy hợp lí nhất). Xong, rất dễ hiểu 🤣 Hết phần "dành cho em bé", nếu bác nào muốn tìm hiểu tiếp thì em xin viết tiếp nhé, còn không thì tới đây thôi được rồi =))

Có thể nói Diffusion model là sự kết hợp từ những ưu điểm của những người tiền nhiệm: Đây là một probabilistic models có nhiệm vụ tạo ra một distribution cho input tương tự như Flow-based model, có khả năng xấp xỉ phân phối của data được sinh ra với phân phối của dữ liệu gốc tương tự như VAE, và có một tầng được pre-determined tương tự như GAN. Tức là, các thế hệ tiền bối có gì thì nó có hết.

Diffusion model bao gồm 2 quá trình: Forward Diffusion Process (mình gọi tắt là FDP) ứng với tầng encoder và Reverse Diffusion Process (mình gọi tắt là RDP) ứng với tầng decoder. Nếu lấy ví dụ là cái tranh kim tuyến ở trên thì FDP là quá trình rắc kim tuyến lên tranh, còn RDP là quá trình "sàng" và phủi bụi kim tuyến đấy. Oke, đi vào từng phần thôi.

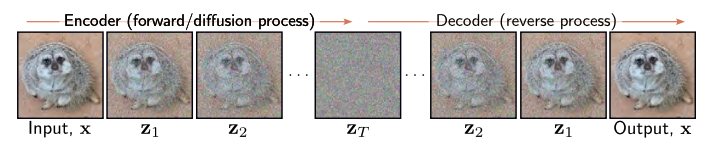
a. Forward Diffusion Process

Đầu tiên là quy trình "rắc kim tuyến lên tranh", aka FDP. Cũng có thể gọi quá trình này là encoder cũng được, nhưng là encoder của Diffusion model. Cho một điểm dữ liệu đầu vào $x_0$ thuộc một phân phối biết trước $x_0 \sim q(x)$ . Quá trình FDP sẽ thêm từ từ theo thời gian (không phải đùng 1 phát đổ hết kim tuyến lên tranh đâu) một lượng nhỏ nhiễu $\epsilon$ được sample từ phân phối Gauss (tức là $\epsilon \sim \mathcal{N}(\mu,\,\sigma^{2})$). Quy trình này có thể được mô tả là:

$$x_1 = \sqrt{1 - \beta_1}x + \sqrt{\beta_1}\epsilon_1$$

$$x_t = \sqrt{1 - \beta_t}x_{t-1} + \sqrt{\beta_t}\epsilon_t$$

Trong đó:

• $\epsilon_t$ là lượng nhiễu được thêm vào $x_t$ tại bước thứ $t \in T$.
• $\beta_t \in [0,1]$ là một hyperparrameter, có nhiệm vụ kiểm soát lượng nhiễu được thêm vào tại mỗi step $t$ (nói vui là tránh lỡ tay đổ hết kim tuyến lên tranh). Thanh niên này còn được gọi là lịch trình phương sai (variance schedule).

Khi mỗi điểm dữ liệu được làm nhiễu như vậy, thì khi đó, ta có thể biểu diễn phân phối của ảnh nhiễu tại hai step liên tiếp $(t-1, t)$ dưới dạng:

$$q(x_t|x_{t-1}) = \mathcal{N}_{x_t}(\sqrt{1 - \beta_t}x_{t-1}, \beta_tI)$$

Từ đó có thể viết gọn quy trình trên như sau:

$$q(x_{1:T}|x_0) = \Pi^T_{t=1}q(x_t|x_{t-1})$$

Có thể thấy vì được thêm vào một lượng nhiễu được sample từ phân phối Gauss nên đến thời điểm $t$ nào đó, distribution của ảnh nhiễu cũng sẽ tuân theo phân phối này với mean $\mu = \sqrt{1 - \beta_t}x_{t-1}$ và variance $\sigma^2 = \beta_tI$.

Nhưng nếu giả sử T rất lớn thì sao nhỉ, tính mấy trăm lần thì tốn tài nguyên quá. Vậy nên ta sẽ dùng một hàm xấp xỉ để tính cho nhanh:

Giả sử ta muốn tính $x_2$ đi, thì ta làm như sau: (Viết giấy luôn chứ viết Latex mệt quá các bác ạ, nếu chữ xấu thì mong các bác bỏ qua ):

Thì làm sao mà từ phương trình (1) mà ra (2) được nhỉ? Nó là như này:

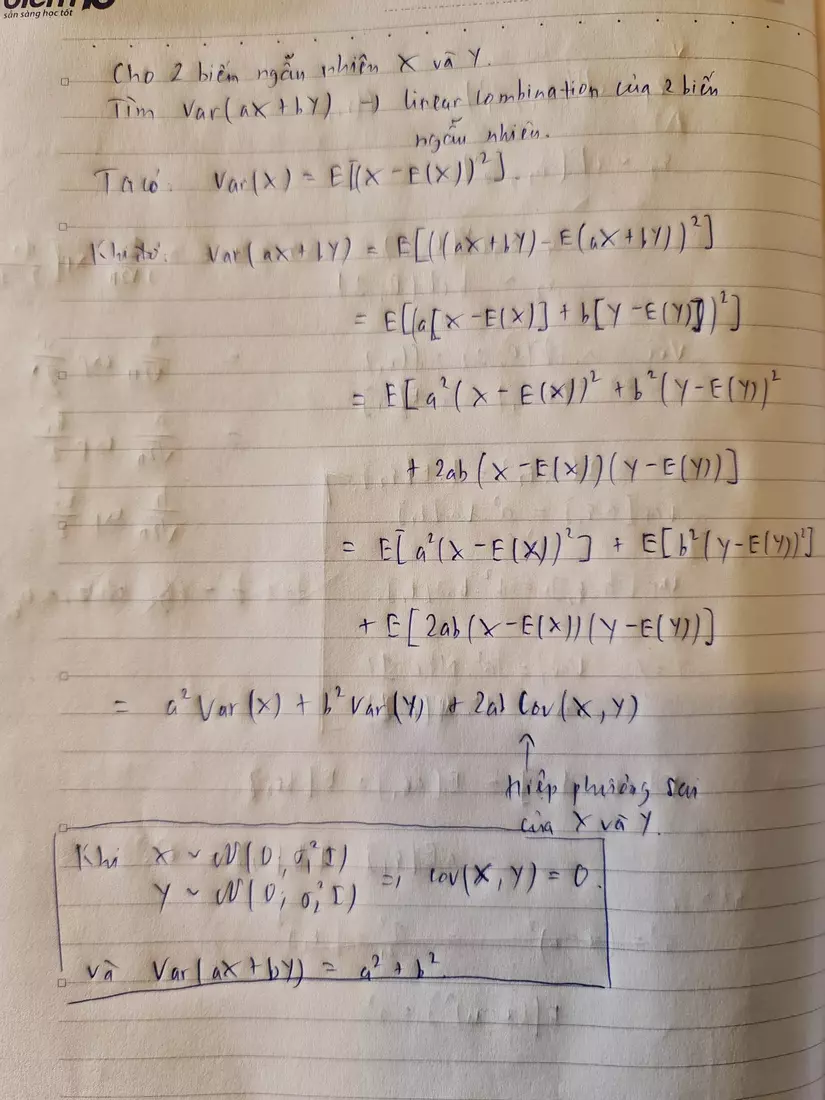
Từ đó, khi chúng ta merge 2 phân phối Gauss với 2 phương sai khác nhau: $\mathcal{N}(0, \sigma^2_1I)$ và $\mathcal{N}(0, \sigma^2_2I)$ thì phân phối Gauss sẽ có dạng $\mathcal{N}(0, (\sigma^2_1 + \sigma^2_2)I)$. Áp dụng vô mô hình FDP thì chúng ta có độ lệch chuẩn là $\sqrt{(1 - \alpha_t) + \alpha_t(1 - \alpha_{t - 1})}$ = $\sqrt{1 - \alpha_t \alpha_{t - 1}}$

Vậy túm cái quần lại, FDP có thể được viết gọn lại như sau:

$$q(x_t|x_0) = \mathcal{N}_{x_t} (\sqrt{\alpha_t}x_0, (1 - \alpha_t)I)$$

Tạm kết

Vì Diffusion model là một mô hình phức tạp nên mình sẽ chia nhỏ ra nhé để tránh bị "bội thực" Phần sau thì mình sẽ viết tiếp về quá trình Reverse Diffusion Process Vậy nhé.

Tài liệu tham khảo

Lilian Weng, What are Diffusion models?

Sergios Karagiannakos, Nikolas Adaloglou, How diffusion models work: the math from scratch