Giải thuật Jaccard
Bài đăng này đã không được cập nhật trong 6 năm
Xin chào mọi người. Lâu lắm rồi mới ngoi lên. Và trong bài này mình sẽ viết về 1 thuật toán được ứng dụng khá nhiều trong các chủ đề AI hay ML là Giải thuật Jaccard(hay gọi tiếng Anh là Jaccard Index). Để tag ML ở bài này cũng hơi láo nhưng bí quá không biết tag gì. Mọi người bỏ qua cho mình.
Khái niệm
Giải thuật Chỉ mục Jaccard, hay còn gọi là giải thuật tỉ lệ của giữa phần giao và phần hợp của 2 tập hợp(có thể gọi tắt hơn nữa nhưng mà....), là 1 giải thuật được đưa ra bởi nhà Toán học Pháp Paul Jaccard. Như đã nói ở trên, giải thuật này là kết quả tính toán độ tương đồng giữa giao của 2 tập hợp và hợp của 2 tập hợp, được tính toán như sau:
Nếu tập và tập đều rỗng, mặc định . Giá trị của luôn phải thoả mãn điều kiện sau:
Độ rời rạc Jaccard lại là để đo tỉ lệ độ rời rạc giữa giao và hợp của 2 tập hợp, được tính bằng cách:
Ý nghĩa
Vậy cái đống công thức toán trên có ý nghĩa gì. Hãy nhìn ảnh sau:
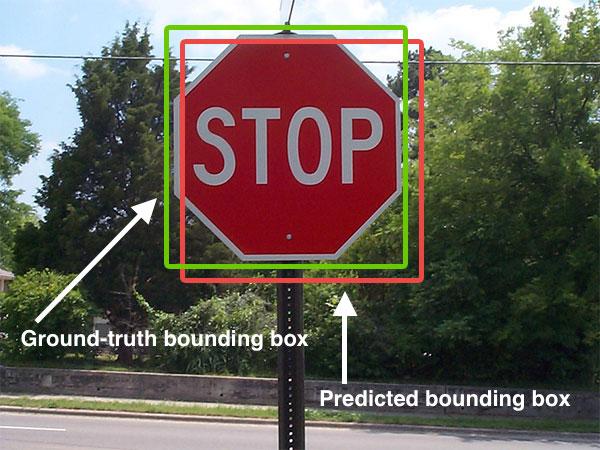
Trong ảnh chúng ta có 2 vùng: vùng xanh là vùng đối tượng thật(gọi là kết quả), vùng đỏ là vùng dự đoán. Muốn dự đoán tốt thì cần phải nhận diện vật thể tốt. 2 vùng này sẽ luôn giao nhau và tổng diện tích sẽ giảm dần. Còn diện tích vùng chung của 2 vùng sẽ tăng dần. Ở đây rõ ràng vùng chung càng lớn thì độ chính xác càng cao, nhưng kéo theo đó diện tích tổng sẽ giảm dần. Chính vì thế J(A, B) càng lớn thì phần tử số sẽ lớn, phần mẫu số sẽ nhỏ. Và phân số này sẽ lớn nhất bằng 1 khi 2 vùng xanh đỏ trùng khớp nhau, và nhỏ nhất bằng 0 khi 2 vùng này hoàn toàn không giao nhau.
Văn phong có vẻ hơi lằng nhằng nhưng bên trên chính là ứng dụng của Jaccard trong object detection. Ngoài ra, Jaccard cũng có thể được ứng dụng trong Recommendation System. Có 3 danh sách diễn viên sau: ={Haruka Kudo, Okuyama Kazusa, Noa Tsurushima}, ={Okuyama Kazusa, Noa Tsurushima, Chika Osaki}, ={Haruka Kudo, Sakurako Okubo, Hiroe Igeta}. Ta có:
| Phần Giao | Phần Hợp |
|---|---|
| ={Okuyama Kazusa, Noa Tsurushima} | ={Haruka Kudo, Okuyama Kazusa, Noa Tsurushima, Chika Osaki} |
| ={} | ={Okuyama Kazusa, Noa Tsurushima, Chika Osaki, Haruka Kudo, Sakurako Okubo, Hiroe Igeta} |
| ={Haruka Kudo} | ={Okuyama Kazusa, Noa Tsurushima, Haruka Kudo, Sakurako Okubo, Hiroe Igeta} |
Dễ thấy theo , , . Ta thấy điểm tương đồng giữa và cao hơn nên có thể lấy diễn viên từ danh sách để gợi ý cho và ngược lại.
Triển khai với code 1
Và sau 1 hồi lý thuyết Toán ở trên(và vài phút để các bạn tra cứu mấy cái tên trên nữa
 ), chúng ta sẽ cùng thử xem triển khai của Jaccard ở trong code như thế nào. Và lần này chúng ta sẽ quay lại 2 ví dụ trên nhưng thứ tự sẽ khác đi. 3 danh sách kia sẽ được chuyển thành 3 mảng A, B, C. Nhiệm vụ chúng ta cần làm ở đây là triển khai thuật toán và đưa ra các cặp có độ tương đồng cao nhất.
), chúng ta sẽ cùng thử xem triển khai của Jaccard ở trong code như thế nào. Và lần này chúng ta sẽ quay lại 2 ví dụ trên nhưng thứ tự sẽ khác đi. 3 danh sách kia sẽ được chuyển thành 3 mảng A, B, C. Nhiệm vụ chúng ta cần làm ở đây là triển khai thuật toán và đưa ra các cặp có độ tương đồng cao nhất.
Đầu tiên là việc cài đặt thuật toán. Việc này khá đơn giản(thực ra cũng có hàm jaccard có sẵn trong python rồi, nhưng chúng ta sẽ thử cài đặt từ đầu)
def jaccard_similarity(list1, list2):
s1 = set(list1)
s2 = set(list2)
return len(s1.intersection(s2)) / len(s1.union(s2))
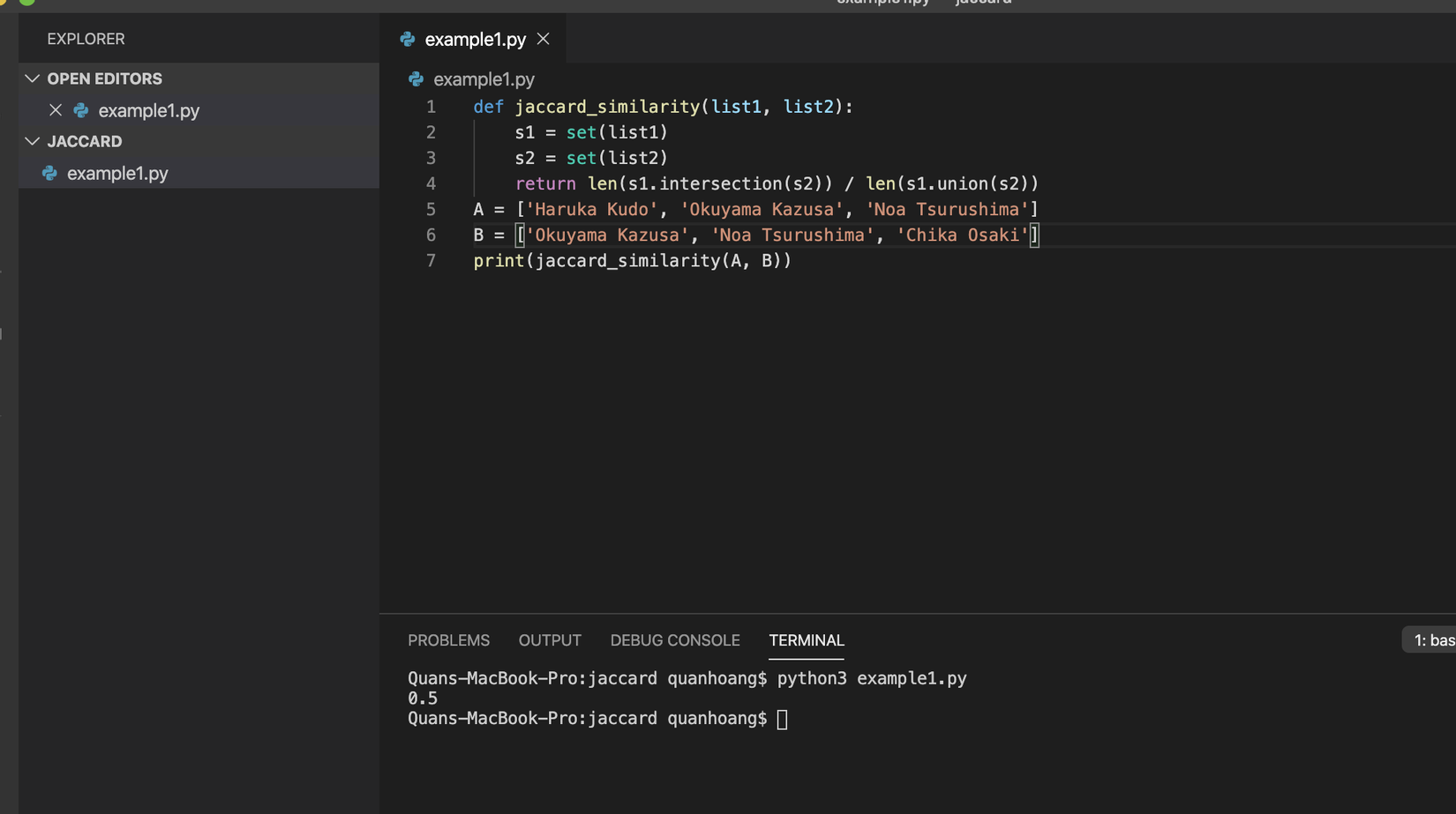
Sau khi có hàm trên, chúng ta sẽ thử nghiệm 2 list như sau:
A = ['Haruka Kudo', 'Okuyama Kazusa', 'Noa Tsurushima']
B = ['Okuyama Kazusa', 'Noa Tsurushima', 'Chika Osaki']
print(jaccard_similarity(A, B))
Và đây là kết quả đạt được. Đúng chuẩn công thức tính toán
Bước tiếp theo cũng đơn giản. Cần vài câu lệnh điều kiện là ổn. Và thế là chúng ta làm tạm đoạn code bẩn sau
def simple_recommender_sys(list1, list2, list3):
J1 = jaccard_similarity(list1, list2)
J2 = jaccard_similarity(list2, list3)
J3 = jaccard_similarity(list3, list1)
if J1 > J2:
if J1 > J3:
print("[",list1,", ",list2,"]")
elif J1 == J3:
print("[",list1,", ",list2,"], [",list1,", ",list3,"]")
else:
print("[",list1,", ",list3,"]")
elif J1 == J2:
if J1 > J3:
print("[",list1,", ",list2,"], [",list2,", ",list3,"]")
elif J1 == J3:
print("[",list1,", ",list2,"], [",list2,", ",list3,"], [",list1,", ",list3,"]")
else:
print("[",list1,", ",list3,"]")
elif J1 < J2:
if J2 > J3:
print("[",list2,", ",list3,"]")
elif J2 == J3:
print("[",list2,", ",list3,"], [",list1,", ",list3,"]")
else:
print("[",list1,", ",list3,"]")
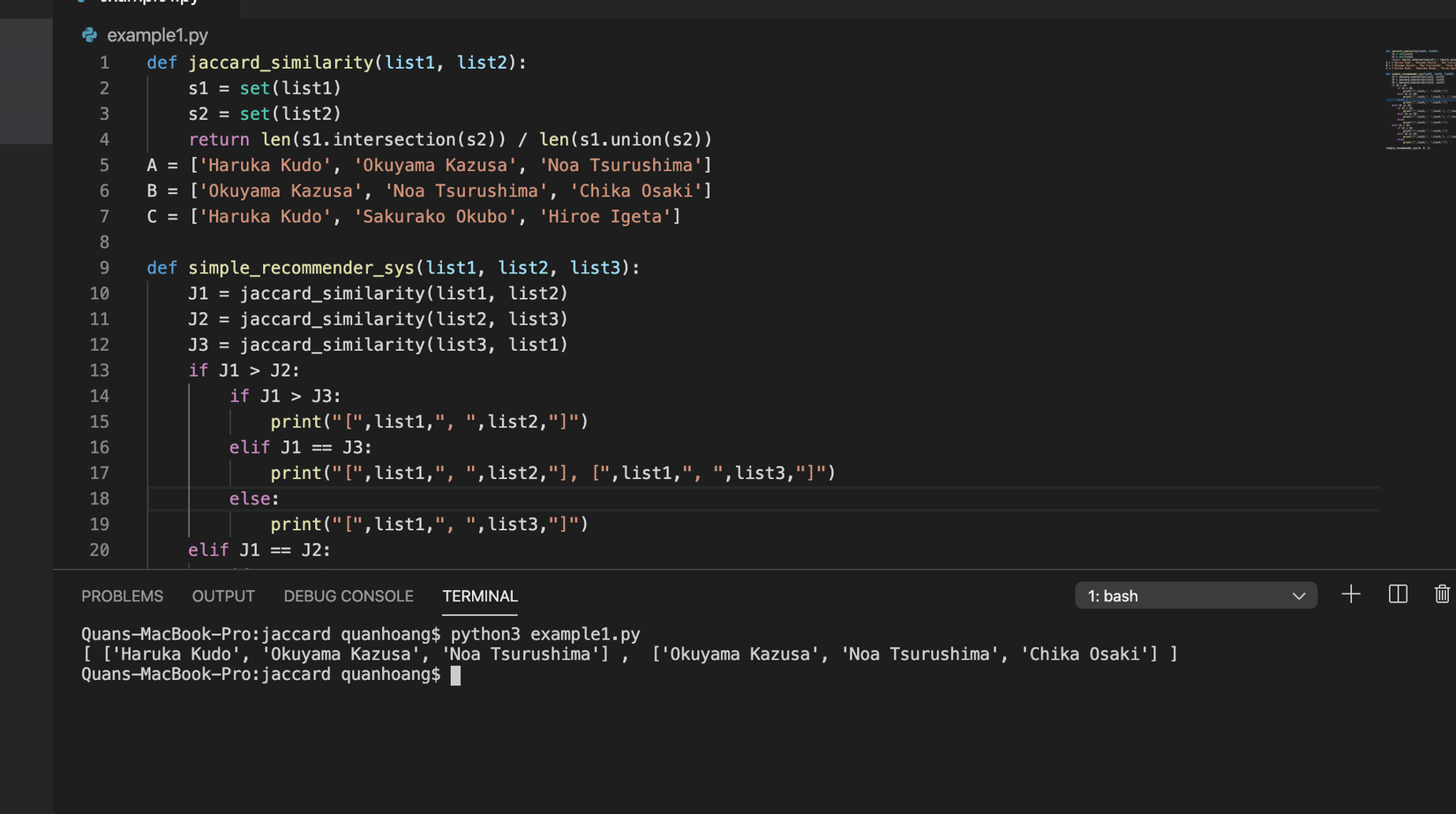
simple_recommender_sys(A, B, C)
Kết quả là A và B được in ra thế này. Trông không đẹp lắm. Nhưng thôi. Đến đây là chúng ta đã xây được 1 hệ gợi ý con con với 3 phần tử rồi. Lên N phần tử các bạn tự tổng quát nhé
Triển khai với code 2
Vâng. Giờ quay lại bài toán object detection.
Trước hết chúng ta sẽ thêm các thư viện cần thiết
# import the necessary packages
from collections import namedtuple
import numpy as np
import cv2
Và để đựng các vật thể trong hộp như trên, thuật toán được viết như sau:
def jaccard_similarity(boxA, boxB):
# determine the (x, y)-coordinates of the intersection rectangle
xA = max(boxA[0], boxB[0])
yA = max(boxA[1], boxB[1])
xB = min(boxA[2], boxB[2])
yB = min(boxA[3], boxB[3])
# compute the area of intersection rectangle
interArea = max(0, xB - xA + 1) * max(0, yB - yA + 1)
# compute the area of both the prediction and ground-truth
# rectangles
boxAArea = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
boxBArea = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
# compute the Jaccard Index value by taking the intersection
# area and dividing it by the sum of prediction + ground-truth
# areas - the interesection area
jaccard_index = interArea / float(boxAArea + boxBArea - interArea)
# return the Jaccard Index value value
return jaccard_index
Ở phần demo, mình lấy tạm 1 cái ảnh nền trắng và vẽ 2 cái hộp ra. Sơ lược hướng dẫn thôi mà
# define the list of example detections
examples = [
Detection("demo.jpg", [39, 63, 203, 112], [54, 66, 198, 114])
]
# loop over the example detections
for detection in examples:
# load the image
image = cv2.imread(detection.image_path)
# draw the ground-truth bounding box along with the predicted
# bounding box
cv2.rectangle(image, tuple(detection.gt[:2]),
tuple(detection.gt[2:]), (0, 255, 0), 2)
cv2.rectangle(image, tuple(detection.pred[:2]),
tuple(detection.pred[2:]), (0, 0, 255), 2)
# compute the Jaccard Index value and display it
jaccard_index = jaccard_similarity(detection.gt, detection.pred)
cv2.putText(image, "Jaccard index: {:.4f}".format(jaccard_index), (10, 30),
cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2)
print("{}: {:.4f}".format(detection.image_path, jaccard_index))
# show the output image
cv2.imshow("Image", image)
cv2.waitKey(0)
Đây là kết quả thu được

Kết bài
Ở bài này, mình chỉ mới giới thiệu các bạn 1 trong các thuật toán được đưa vào trong AI/ML cũng như đào 1 tí về bản chất toán học của AI. Đây là link source code của mình: https://github.com/BlazingRockStorm/Jaccard_Index_Algorithm
Tham khảo
https://en.wikipedia.org/wiki/Jaccard_index https://www.pyimagesearch.com/2016/11/07/intersection-over-union-iou-for-object-detection/
All rights reserved