P1: Tổng quan về Graph

1. Tổng quan về Graph

Trong phần này, mình sẽ giới thiệu tổng quan về kiểu dữ liệu Graph trong khoa học máy tính, cũng như một số thuộc tính, tính chất cơ bản cần chú ý khi làm việc với kiểu dữ liệu này trong Machine Learning/Deep Learning nhé. Nếu mà phân tích tất tần tật tuốt tuồn tuột các thuật toán của Graph thì sẽ dài như sông Mê Kông ấy nên mình chỉ tập trung giới thiệu ngắn gọn thôi nhé, còn những thuật toán cổ điển thì....để sau.

Nói thật, mình không biết phải dịch từ "Graph" sang tiếng Việt như thế nào. Có bạn sẽ dịch là "đồ thị" nhưng mình lại thấy từ "chart" mới chỉ đúng bản chất của "đồ thị". Vậy nên, mình không dịch từ này sang tiếng Việt nhé. Ồ kế.

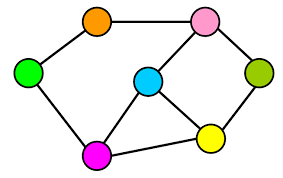
Graph là kiểu dữ liệu non-linear được tạo thành từ 2 thành phần cơ bản: các cạnh (edge) và các nốt (node/vertex). Graph được xem như là kiểu dữ liệu phù hợp khi bạn muốn phân tích hoặc biểu diễn mối quan hệ giữa các thực thể với nhau. Graph thường được kí hiệu là G(V,E) .Trong đó:

Node (còn gọi là vertex, kí hiệu là V) là đơn vị cơ bản cấu thành nên Graph. Đây là nơi lưu trữ thông tin của một thực thể, một đối tượng nào đó mà bạn muốn phân tích. Một node có thể được gắn nhãn hoặc không.
Edge (gọi nôm na là cạnh, kí hiệu là E) là kết nối giữa hai node với nhau. Các kết nối cũng có thể là kết nối trơn (tức là chỉ đơn giản là nối 2 node lại với nhau) hoặc biểu diễn một đặc trưng, mối liên hệ gì đó giữa hai node.

Có nhiều cách phân chia các loại Graph. Tuy nhiên, dựa vào các cạnh của Graph thì Graph được chia ra thành 2 loại chính:

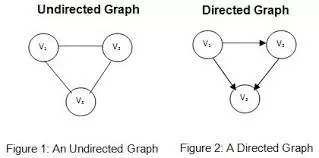
Undirected Graph: Là Graph mà các cạnh của nó chỉ đơn giản là nối 2 node lại với nhau.
Directed Graph: Là Graph mà các cạnh của nó có 1 hướng cụ thể (giống như 1 vector ấy).

Ngoài ra các cạnh của một graph có thể được đánh trọng số, tùy vào bài toán mình đang thực hiện.

alt

2. Một số định nghĩa của Graph

Ở đây thì mình sẽ trình bày một số định nghĩa của Graph mà sau này có sử dụng khá nhiều trong Machine Learning nhé.

a. Adjacency Matrix

Lại một lần nữa, mình lại không biết dịch từ này ra tiếng Việt là gì, ai có cách dịch hay thì chỉ cho mình biết với nhé 😁 Hiểu đơn giản, Adjacency Matrix (ký hiệu là A) là ma trận biểu diễn các cạnh nối các node trong 1 Graph. Trong đó, $A_{ij}$ = 1 khi có một cạnh nối giữa 2 node i và node j, bằng 0 khi ngược lại.

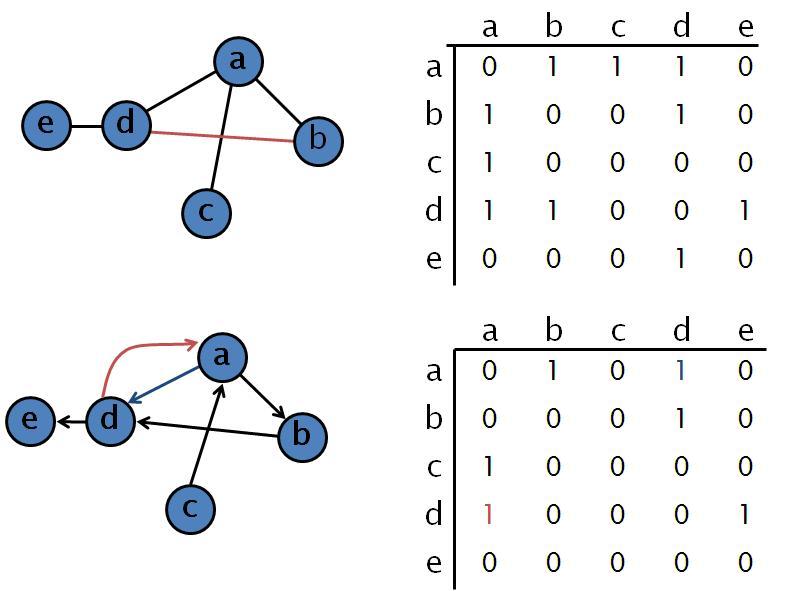
Hình trên biểu diễn Adjacency Matrix của một Undirected Graph (Graph trên) và Directed Graph (Graph dưới). Hi vọng mọi người tưởng tượng được.

b. Node Degree

Node Degree (kí hiệu là $k_i$ ) có thể hiểu là số lượng cạnh được kết nối tới một node. Cùng nhìn lại hình ở trên nhé.

Đối với Undirected Graph: ví dụ ta có $k_A$ = 3, $k_C$ = 1. Từ đó ta có giá trị average degree của một Undirected Graph được tính theo công thức Avg(k) = $\frac{2E}{N}$ .
Đối với Directed Graph thì ta có in-degree (tức số lượng edge hướng tới một node) và out-degree (số lượng edge từ node đó hướng tới các node khác). Lấy ví dụ cũng ở hình trên, xét node b, ta thấy $k_{in}^{b}$ =1 (chỉ có 1 cạnh từ a tới b) và $k_{out}^{b}$ =1(chỉ có 1 cạnh từ b tới c). Khi đó node-degree của node b sẽ là $k_{in}^{b} + k_{out}^{b}$ = 2 và average degree của một Directed Graph được tính theo công thức Avg(k) = $\frac{E}{N}$ .

c. Path

Path hiểu đơn giản là toàn bộ các cạnh có trên đường đi từ node này tới node kia. Lấy ví dụ trong cái Undirected Graph cũng ở hình trên luôn nhé, ta thấy b-a-d-e là một path biểu diễn đường đi từ node b tới node e.

3. Graph trong cuộc sống

Trong đời sống thường ngày, kiểu dữ liệu Graph rất phổ biến đó. Từ những thứ nhỏ tí ti như cấu trúc phân tử của các hợp chất hóa học, đến những thứ rộng lớn như các mạng xã hội, hệ thống viễn thông, v.v. Tất cả đều có thể được biểu diễn bằng Graph.