1. Tổng quan bài viết này

Đây là series thứ 3 về giới thiệu diffussion model , trong bài viết này mình sẽ hướng dẫn code về diffussion model . Chúng ta sẽ bắt đầu với bài báo DDPM(Denoising Diffusion Probabilistic Models) , trong bài viết này chúng ta sẽ dử dụng framework tensorflow . Trước khi bắt đầu bài viết chúng ta sẽ nhắc lại chút kiến thức từ Series 2 về mình sẽ cập nhật thêm một số kiến thức còn thiếu trong series 2 để chúng ta củng cố cho bài học này.

1.1 . Tóm tắt khuyến tán thuận(Forward process)

Hình 1: Hình vẽ biểu thị quy trình khuyến tán với mũi tên màu đen ám chỉ quy trình khuyến tán thuận và mũi tên màu xanh là quá trình khuyến tán ngược . Màu hồng ám chỉ rằng mũi tên màu xanh và màu hồng phải có cùng giá trị mà ta quan tâm.

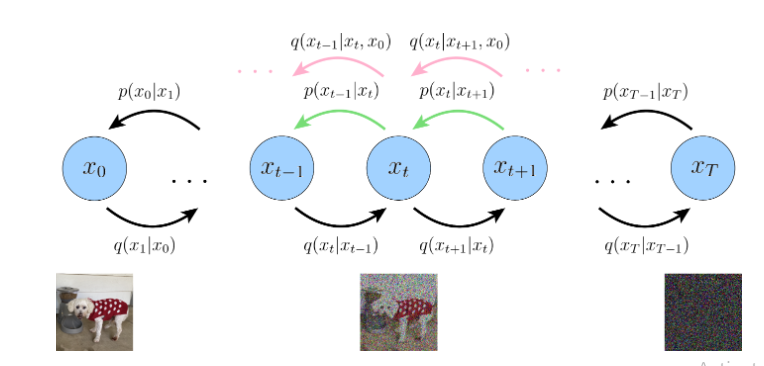
Đầu tiên chúng ta sẽ bắt đầu với khuyên tán thuận .Được miêu tả như sau:

(1)

$$q ( x _ { 1 :T} | x _ { 0 } ) = \prod _ { t = 1 } ^ { T} q ( x _ { t } | x _ { t + 1 } )$$

mà:

(2)'

$$q ( x _ { t } | x _ { t - 1 } ) = N ( x _ { t } ; \sqrt { \alpha _ { t } } x _ { t - 1 } , ( 1 - \alpha _ { t } ) I = x_{t})$$

Khi đó ta có thể tính reparameter trick:

(3)

$$x_{t} = \sqrt { \overline { \alpha } } _ { t} x _ { 0 } + \sqrt { 1 - \overline { \alpha } } _ { t } \epsilon _ { 0 }$$

Từ reparameter trick ta áp dụng quy tắc bayess từ series2 để tính trung bình của mọi ảnh noise tiếp theo dụa trên đầu vào ảnh $x_{0}$

(4)

$$\mu _ { q} \left ( x _ { t } , x _ { 0 } \right ) = \frac { \sqrt { \alpha _ { t } } \left ( 1 - \overline { \alpha } _ { t - 1 } \right ) x_ { t} + \sqrt { \overline { \alpha } _ { t - 1 } } \left ( 1 - \alpha _ { t } \right ) x_ { 0 } } { 1 - \overline { \alpha } _ { t} }$$

(5)

$$\mu _ { \theta } ( x _ { t } , t ) = \frac { \sqrt { \alpha _ { t } } ( 1 - \overline { \alpha } _ { t - 1 } ) x _ { t } + \sqrt { \overline { \alpha } _ { t - 1 } } ( 1 - \alpha _ { t } ) \hat { x } _ { \theta } ( x _ { t } , t ) } { 1 - \overline { \alpha _ { t } } }$$

1.2. Tóm tắt Khuyến tán ngược(Reverse process)

Như chúng ta đã biết từ phương trình số (33) trong series 2 thì hàm loss được viết như sau:

Hình 2: Mô tả hàm loss function từ series của mô hình diffussion model

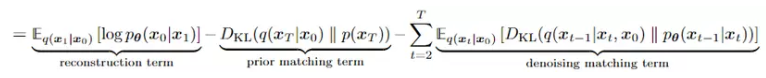
Từ phương trình số (3) ta biết được rằng ta có thể tính toán reparameter trick của khuyến tán ngược lại đây được gọi là quá trình lấy mẫu . (Get sample) , trong DDPM bạn nên nhớ một điều rằng bảo toàn phương sai tức phương sai của mọi bước thời gian t với ${t = [1,t]}$ luôn không bao giờ thay đổi và chúng luôn bằng 1. Từ đó ta có thể tính toán ngược lại và hơn hết là Học parameter của trung bình $\mu_{t}$ . Đây sẽ là quá trình lấy mẫu để dự đoán ra ảnh từ tham số đã học được

(6)

$$x _ { 0 } = \frac { x _ { t } - \sqrt { 1 - \alpha _ { t } } \epsilon _ { 0 } } { \sqrt { \overline { \alpha } _ { t } } }$$

(7) thay (6) vào phương trình (4)

$$\mu _ { q } ( x _ { t } , x _ { 0 } ) = \frac { \sqrt { \alpha _ { t } } ( 1 - \overline { \alpha } _ { t - 1 } ) x _ { t } + \sqrt { \overline { \alpha } _ { t - 1 } } ( 1 - \alpha _ { t } ) x _ { 0 } } { 1 - \overline { \alpha } _ { t } }$$

(8)

$$\frac { \sqrt { \alpha _ { t } } ( 1 - \overline { \alpha } _ { t - 1 } ) x _ { t } + \sqrt { \overline { \alpha } _ { t - 1 } } ( 1 - \alpha _ { t } ) \frac { x _ { t } - \sqrt { 1 - \alpha _ { t } } \epsilon _ { 0 } } { \sqrt { \overline { \alpha } _ { t } } } } { 1 - \overline { \alpha } _ { t } }$$

(9)

$$\frac { \sqrt { \alpha _ { t } } ( 1 - \overline { \alpha } _ { t - 1 } ) x _ { t } + ( 1 - \alpha _ { t } ) \frac { x _ { t } - \sqrt { 1 - \alpha _ { t } } \epsilon _ { 0 } } { \sqrt { \overline { \alpha } _ { t } } } } { 1 - \overline { \alpha } _ { t } }$$

(10)

$$\frac { \sqrt { \alpha _ { t } } ( 1 - \overline { \alpha } _ { t - 1 } ) x _ { t } } { 1 - \overline { \alpha } _ { t } } + \frac { ( 1 - \alpha _ { t } ) x _ { t } } { ( 1 - \overline { \alpha } _ { t } ) \sqrt { \alpha _ { t } } } - \frac { ( 1 - \alpha _ { t } ) \sqrt { 1 - \overline { \alpha } _ { t } } \epsilon _ { 0 } } { ( 1 - \overline { \alpha } _ { t } ) \sqrt { \alpha _ { t } } }$$

(11)

$$( \frac { \sqrt { \alpha _ { t } } ( 1 - \overline { \alpha } _ { t - 1 } ) } { 1 - \overline { \alpha } _ { t } } + \frac { 1 - \alpha _ { t } } { ( 1 - \overline { \alpha } _ { t } ) \sqrt { \alpha _ { t } } } ) x _ { t } - \frac { ( 1 - \alpha _ { t } ) \sqrt { 1 - \overline { \alpha } _ { t } } } { ( 1 - \overline { \alpha } _ { t } ) \sqrt { \alpha _ { t } } } \epsilon _ { 0 }$$

(12)

$$( \frac { \alpha _ { t } ( 1 - \overline { \alpha } _ { t - 1 } ) } { ( 1 - \overline { \alpha } _ { t } ) \sqrt { \alpha _ { t } } } + \frac { 1 - \alpha _ { t } } { ( 1 - \overline { \alpha } _ { t } ) \sqrt { \alpha _ { t } } } ) x _ { t } - \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \overline { \alpha } _ { t } } \sqrt { \alpha _ { t } } } \epsilon _ { 0 }$$

(13)

$$\frac { \alpha _ { t } - \overline { \alpha } _ { t } + 1 - \alpha _ { t } } { ( 1 - \overline { \alpha } _ { t } ) \sqrt { \alpha _ { t } } } x _ { t } - \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \overline{ \alpha } _ { t } } \sqrt { \alpha _ { t } } } \epsilon _ { 0 }$$

(14)

$$\frac { 1 - \overline { \alpha } _ { t } } { ( 1 - \overline { \alpha } _ { t } ) \sqrt { \alpha _ { t } } } x _ { t } - \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \overline { \alpha } _ { t } } \sqrt { \alpha _ { t } } } \epsilon _ { 0 }$$

(15)

$$\frac { 1 } { \sqrt { \alpha _ { t } } } x _ { t } - \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \overline\alpha _ { t } } \sqrt { \alpha _ { t } } } \epsilon _ { 0 }$$

(16) Từ đó suy ra

$$\mu _ { \theta } ( x _ { t } , t ) = \frac { 1 } { \sqrt { \alpha _ { t } } } x _ { t } - \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \overline\alpha _ { t } } \sqrt { \alpha _ { t } } }\hat { \epsilon } _ { \theta } ( x _ { t } , t )$$

1.3 Tóm tắt Hàm loss Function

Sau khi đã xong bước lấy mẫu chúng ta sẽ thực hiện tiếp bước rút gọn hàm loss từ series 2 và dựa trên hình 2:

$$\log p_{ \theta } ( x _ { 0 } | x _ { 1 } )$$

Trong hàm loss funtion của chúng ta , ta sẽ bỏ qua điều này . Vì chúng sẽ được thực hiện bên ngoài quá trình đào tạo và nằm trong quá trình lấy mẫu. Trong bài báo tắc giả đã tóm gọn hàm loss và bỏ qua chúng , nói ngắn gọn hơn việc tối ưu hóa hàm loss sẽ phụ thuộc vào khoảng cách phân kỳ giữa noise ảnh khuyến tán thuận và noise ảnh khuyến tán ngược . Chúng gần bằng 0 thì tất cả sẽ đáp ứng được nhu câu trên.

(17)

$$\underset { \theta } { \arg \min D _ { K L } } ( q ( x _ { t - 1 } | x _ { t } , x _ { 0 } ) \| p _ { \theta } ( x _ { t - 1 } | x _ { t } ) )$$

(18)

$$= \underset { \theta } { \arg \min } \frac { 1 } { 2 \sigma _ { q } ^ { 2 } ( t ) } [ \| \mu _ { \theta } - \mu _ { q } \| _ { 2 } ^ { 2 } ]$$

Dựa trên (15) và (16) ta có: (19)

$$= \underset { \theta } { \arg \min } \frac { 1 } { 2 \sigma _ { q } ^ { 2 } ( t ) } [\| \frac { 1 } { \sqrt { \alpha _ { t } } } x _ { t } - \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \overline { \alpha } _ { t } } {\sqrt { \alpha } _ { t }}} \hat { \epsilon } _ { \theta } ( x _ { t } , t ) - \frac { 1 } { \sqrt { \alpha _ { t } } } x _ { t } + \frac { 1 - \alpha _ { t } } { \sqrt { \alpha _ { t } } \sqrt{1-\overline\alpha}} \epsilon _ { 0 }\| ^{2} ]$$

(20)

$$= \underset { \theta } { \arg \min } \frac { 1 } { 2 \sigma _ { q } ^ { 2 } ( t ) } [\| \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \dot { \alpha } _ { t } } \sqrt { \alpha _ { t } } } \epsilon _ { 0 } - \frac { 1 - \alpha _ { t } } { \sqrt { 1 - \overline{ \alpha } _ { t } } \sqrt { \alpha _ { t } } } \hat { \epsilon } _ { \theta } ( x _ { t } , t ) \| _ { 2 } ^ { 2 }]$$

(21)

$$= \underset { \theta } { \arg \min } \frac { 1 } { 2 \sigma _ { q } ^ { 2 } ( t ) } \frac { ( 1 - \alpha _ { t } ) ^ { 2 } } { ( 1 - \overline { \alpha } _ { t } ) \alpha _ { t } } [ \| \epsilon _ { 0 } - \hat { \epsilon } _ { \theta } ( x _ { t } , t ) \| _ { 2 } ^ { 2 } ]$$

Ở đây, ${\hat\epsilon_{\theta}(x_{t},t)}$ là một mạng nơron học cách dự đoán noise từ T với gausian tiêu chuẩn x. Do đó chúng ta biết rằng mạng nơ ron dự đoán ra ảnh gốc ${x_{0}}$ giống như dự đoán noise , hơn nữa tác giả đã thử nghiệm nhận thấy rằng việc dự đoán noise sẽ mang lại hiểu quả tốt hơn . Đó là lý do tại sao trong phương trình số (33) ta bỏ qua ${\log p_{ \theta } ( x _ { 0 } | x _ { 1 } )}$.

(22) Tổng kết gói gọn như trong paper

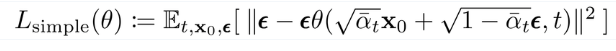
2. Thực Hành Code với DDPM

Ta sẽ thực hiện quá trình code diffussion model dựa trên 2 bảng tổng kết của DDPM đã ghi. Hình *

2.1 Thực hiện với kiến trúc UNet

Tải thư viện về jupyternotebook hoặc trên colab

!pip install tensorflow_addons

Xây dựng Unet

import tensorflow as tf
import tensorflow_addons as tfa
import math
import tensorflow_datasets as tfds
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

class SelfAttention(tf.keras.layers.Layer):
    def __init__(self, channels,**kwargs):
        super(SelfAttention, self).__init__()
        self.channels = channels
        self.mha = tf.keras.layers.MultiHeadAttention(num_heads = 4,key_dim=self.channels)
        self.ln = tf.keras.layers.LayerNormalization()
        self.ff_self = tf.keras.Sequential([
            tf.keras.layers.LayerNormalization(),
            tf.keras.layers.Dense(channels),
            tfa.layers.GELU(),
            tf.keras.layers.Dense(channels)
        ]
        )
    def build(self,x):
        self.reshape1 = tf.keras.layers.Reshape((x[1]*x[2],self.channels))
        self.reshape2 = tf.keras.layers.Reshape((x[1],x[2],self.channels))
    def call(self, x):

        x = self.reshape1(x)
        x_ln = self.ln(x)

        attention_value = self.mha(x_ln, x_ln, x_ln)
        
        attention_value = attention_value + x
        
        attention_value = self.ff_self(attention_value) + attention_value
        
        return self.reshape2(attention_value)

class DoubleConv(tf.keras.layers.Layer):
    def __init__(self, out_channels, mid_channels=None, residual=False):
        super(DoubleConv,self).__init__()
        self.residual = residual
        if not mid_channels:
            mid_channels = out_channels
        self.double_conv = tf.keras.Sequential([
            tf.keras.layers.Conv2D(mid_channels, kernel_size=3, padding='same', use_bias=False),
            tfa.layers.GroupNormalization(1),
            tfa.layers.GELU(),
            tf.keras.layers.Conv2D(out_channels, kernel_size=3, padding='same', use_bias=False),
            tfa.layers.GroupNormalization(1)
        ]
        
        )
        self.gelu = tfa.layers.GELU()

    def call(self, x):
        if self.residual:
            return self.gelu(x + self.double_conv(x))
        else:
            return self.double_conv(x)
  
  class SILU(tf.keras.layers.Layer):
    def __init__(self,**kwargs):
        super(SILU,self).__init__()
        self.sigmoid = tf.keras.layers.Activation("sigmoid")
    def call(self,x):
        theta = 1.0
        return x* self.sigmoid(theta*x)
 
 class Down(tf.keras.layers.Layer):
    def __init__(self, in_channels, out_channels):
        super(Down,self).__init__()

        self.maxpool_conv = tf.keras.Sequential(
            [
            tf.keras.layers.MaxPool2D(pool_size=(2,2)),
            DoubleConv(in_channels,residual=True),
            DoubleConv(out_channels)
        ]
        )

        self.emb_layer = tf.keras.Sequential([
            SILU(),
            tf.keras.layers.Dense(out_channels)]
        )

    def repeat(self,t,x):
        t = t[:,None,None,:]

        t = tf.repeat(t,[x.shape[1]],axis=1)
        t = tf.repeat(t,[x.shape[2]],axis=2)
        return t
    def call(self, x, t):
        
        x = self.maxpool_conv(x)
        t = self.emb_layer(t)
        emb =  self.repeat(t,x)

        return x + emb
 
 class Up(tf.keras.layers.Layer):
    def __init__(self, in_channels, out_channels):
        super(Up,self).__init__()

        self.up = tf.keras.layers.UpSampling2D(size=2,interpolation="bilinear")
        self.conv = tf.keras.Sequential(
            [
            DoubleConv(in_channels,residual=True),
            DoubleConv(out_channels,in_channels//2)
        ]
        )

        self.emb_layer = tf.keras.Sequential([
            SILU(),
            tf.keras.layers.Dense(out_channels)  
        ]
        )
        self.concat = tf.keras.layers.Concatenate(axis=-1)

    def repeat(self,t,x):
        t = t[:,None,None,:]

        t = tf.repeat(t,[x.shape[1]],axis=1)
        t = tf.repeat(t,[x.shape[2]],axis=2)
        return t

    def call(self, x, skip_x,t):
        x = self.up(x)
        x = self.concat([skip_x,x])
        x = self.conv(x)      
        t = self.emb_layer(t)
        emb =  self.repeat(t,x)
        return x + emb
 
 class Encoding(tf.keras.layers.Layer):
    def __init__(self,**kwargs):
        super(Encoding,self).__init__()
        
    def call(self,t,channels):
        inv_freq = 1.0 / (10000 ** (np.arange(start=0, stop = channels, step=2)/ channels))
        t = tf.cast(t[...,tf.newaxis],dtype=tf.double)

        pos_enc_a = tf.math.sin(inv_freq * tf.repeat(t,repeats=[channels//2],axis=-1))
        pos_enc_b = tf.math.cos(inv_freq * tf.repeat(t,repeats=[channels//2],axis=-1))

        pos_enc = tf.concat([pos_enc_a, pos_enc_b], axis=-1)
        return pos_enc
 
 class UNet(tf.keras.Model):
    def __init__(self, c_in=1, c_out=1, time_dim=256,**kwargs):
        super(UNet,self).__init__()

        self.time_dim = time_dim
        self.inc = DoubleConv(64)
        self.down1 = Down(64, 128)
        self.sa1 = SelfAttention(128)
        self.down2 = Down(128, 256)
        self.sa2 = SelfAttention(256)
        self.down3 = Down(256, 256)

        self.bot1 = DoubleConv(512)
        self.bot2 = tf.keras.layers.MultiHeadAttention(num_heads = 4,key_dim=512)
        self.bot3 = DoubleConv(256)

        self.up1 = Up(512, 128)
        self.sa3 = SelfAttention(128)
        self.up2 = Up(256, 64)
        self.sa4 = SelfAttention(64)
        self.up3 = Up(128, 64)
        self.outc = tf.keras.layers.Conv2D(c_out, kernel_size=1)
        self.pos_encoding = Encoding()

    def call(self, x, t):
        t = self.pos_encoding(t, self.time_dim)
        x1 = self.inc(x)
        
        x2 = self.down1(x1, t)
        x2 = self.sa1(x2)
        x3 = self.down2(x2, t)
        x3 = self.sa2(x3)
        x4 = self.down3(x3, t)

        x4 = self.bot1(x4)
        x4 = self.bot2(x4,x4,x4)
        x4 = self.bot3(x4)

        x = self.up1(x4, x3, t)
        x = self.sa3(x)     
        x = self.up2(x, x2, t)
        x = self.sa4(x)
        x = self.up3(x, x1, t)
        output = self.outc(x)
        return output

2.2 Hyparameter

Chúng ta tiếp theo sẽ là các Hyparameter. Hình 3: Mô tả alpha_bar(Khuyến tán thuận)

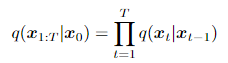
Hình 4: Mô tả trung bình tổng thể sqrt_alpha_bar

Hình 5: Mô tả phương sai one_minus_sqrt_alpha_bar

# HYPARAMETER

# data
num_epochs = 50  # train for at least 50 epochs for good results
image_size = 32

# optimization
batch_size = 256
learning_rate = 1e-3
weight_decay = 1e-4

# model
timesteps = 500 # Số bước thời gian T bạn có thể đặt tùy ý như DDPM trong bài báo là 1000 nhưng đây minh đặt theo cảm hứng
a_min = 0.0001 #  
a_max = 0.02   # 

# create a fixed beta schedule
beta = np.linspace(a_min,a_max, timesteps+1) lịch trình phương sai như trong series 2

# this will be used as discussed in the reparameterization trick
alpha = 1 - beta # Đặt alpha = 1-beta
alpha_bar = np.cumprod(alpha, 0) # Tính toán tích tất cả các alpha
alpha_bar = np.concatenate((np.array([1.]), alpha_bar[:-1]), axis=0) #a_0 = 1
sqrt_alpha_bar = np.sqrt(alpha_bar)
one_minus_sqrt_alpha_bar = np.sqrt(1-alpha_bar)

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()

2.3 Data Sequence tensorflow

Tiền xử lý data bạn có thể tự do tùy chỉnh data tự do. Trong bài viết này mình đã test thử fashion_mnist.

class DataGenerator(tf.keras.utils.Sequence):
   def __init__(self,img_paths,image_size,batch_size,dim=(28,28),n_channels=1,shuffle=True):
       self.dim = dim
       self.batch_size = batch_size
       self.image_size = [image_size,image_size]
       self.img_paths = img_paths
       self.n_channels = n_channels
       self.shuffle = shuffle
       self.img_indexes = np.arange(len(self.img_paths))
       self.on_epoch_end()
       
   def __len__(self):
       'Denotes the number of batches per epoch'
       return int(np.floor(len(self.img_indexes) / self.batch_size))

   def __getitem__(self, index):
       'Generate one batch of data'
       # Generate indexes of the batch
       indexes = self.indexes[index*self.batch_size:(index+1)*self.batch_size]

       # Find list of IDs
       list_IDs_temps = [self.img_indexes[k] for k in indexes]

       # Generate data
       X = self.__data_generation(list_IDs_temps)
       return X
   def on_epoch_end(self):
       'Updates indexes after each epoch'
       self.indexes = np.arange(len(self.img_paths))
       if self.shuffle == True:
           np.random.shuffle(self.indexes)
   def __data_generation(self, list_IDs_temps):
       X = np.empty((self.batch_size, *self.dim))

       for i, ID in enumerate(list_IDs_temps):
           X[i,] = self.img_paths[ID]
       X = X[:,:,:, np.newaxis]
       X = tf.image.resize(X,size = self.image_size)
       X = tf.cast(X/255.0,dtype=tf.float32)
       return X

2.4 Khuyến tán thuận và Repameter trick

Tiếp theo là phần cực kỳ quan trọng đó chình là quá trình khuyến tán thuận của mô hình reparameter trick Hình 6: Mô tả reparameter trick

class Forward_Noise(tf.keras.layers.Layer):

def __init__(self,sqrt_alpha_bar,one_minus_sqrt_alpha_bar,**kwargs):
  super(Forward_Noise,self).__init__(**kwargs)
  self.sqrt_alpha_bar = sqrt_alpha_bar
  self.one_minus_sqrt_alpha_bar = one_minus_sqrt_alpha_bar

def forward_noise(self,x_0,t):
  noise = tf.random.normal(x_0.shape)
  reshaped_sqrt_alpha_bar_t = tf.cast(tf.experimental.numpy.reshape(tf.experimental.numpy.take(self.sqrt_alpha_bar, t), (-1, 1, 1, 1)),tf.float32) # trung bình tổng thể
  reshaped_one_minus_sqrt_alpha_bar_t = tf.cast(tf.experimental.numpy.reshape(tf.experimental.numpy.take(self.one_minus_sqrt_alpha_bar, t), (-1, 1, 1, 1)),tf.float32) # phương sai
  noisy_image = reshaped_sqrt_alpha_bar_t  * x_0 + reshaped_one_minus_sqrt_alpha_bar_t  * noise # Reparameter trick
  return noisy_image,noise

def call(self,x_0,t):
  noise_img,noise = self.forward_noise(x_0,t)
  return noise_img,noise

class Generator(tf.keras.layers.Layer):
def __init__(self,timesteps,**kwargs):
  super(Generator,self).__init__()
  self.timesteps = timesteps
  
def generate_timestamp(self,num):
  return tf.random.uniform(shape=[num], minval=0, maxval=self.timesteps, dtype=tf.int32)
def call(self,x):
  x = self.generate_timestamp(x)
  return x
  

Hiển thị thông tin khuyến tán thuận khi noise ảnh dần với gaussian.

forward_noise = Forward_Noise(sqrt_alpha_bar,one_minus_sqrt_alpha_bar)
generate_timestamp = Generator(timesteps)
train_generator = DataGenerator(x_train, image_size = image_size,batch_size =batch_size,shuffle=True)
val_generator = DataGenerator(x_test,image_size = image_size,batch_size=batch_size,shuffle=True)
# Let us visualize the output image at a few timestamps
sample_mnist = train_generator.__getitem__(1)[0]
fig = plt.figure(figsize=(32,50))

for index, i in enumerate([0,50,100,150,200,250,300,350,400,450,500]):
  noisy_im, noise = forward_noise(sample_mnist, np.array([i,]))
  plt.subplot(1, 11, index+1)
  plt.imshow(np.squeeze(noisy_im))
plt.show()

Hiinh 7: Quá trình khuyến tán thuân bạn sẽ nhận thấy rằng DDPM có một nhược điểm mà sau này DDIM đã khắc phục được chúng.

2.5 Train Model

Chekpoint model

# create our checkopint manager
ckpt = tf.train.Checkpoint(net=net)
ckpt_manager = tf.train.CheckpointManager(ckpt, "./checkpoints", max_to_keep=2)

# load from a previous checkpoint if it exists, else initialize the model from scratch

if ckpt_manager.latest_checkpoint:
  ckpt.restore(ckpt_manager.latest_checkpoint)
  start_interation = int(ckpt_manager.latest_checkpoint.split("-")[-1])
  print("Restored from {}".format(ckpt_manager.latest_checkpoint))
else:
  print("Initializing from scratch.")

loss_fn = tf.keras.losses.MeanSquaredError()
# Prepare the metrics.
train_acc_metric = tf.keras.metrics.MeanSquaredError('mse train')
val_acc_metric = tf.keras.metrics.MeanSquaredError('mse val')
# Optimizers
opt = tfa.optimizers.AdamW(
      learning_rate=learning_rate, weight_decay=weight_decay)

Train model.

@tf.function
def train_step(batch):   
   timestep_values = generate_timestamp(batch.shape[0])
   noised_image, noise = forward_noise(batch, timestep_values)
   with tf.GradientTape() as tape:
       prediction = net(noised_image, timestep_values)
       
       loss_value = loss_fn(noise, prediction)
   
   gradients = tape.gradient(loss_value, net.trainable_variables)
   opt.apply_gradients(zip(gradients, net.trainable_variables))
   train_acc_metric.update_state(noise,prediction)
   return loss_value

@tf.function
def test_step(batch):
   timestep_values = generate_timestamp(batch.shape[0])

   noised_image, noise = forward_noise(batch, timestep_values)
   
   prediction = net(noised_image, timestep_values)
   loss_value = loss_fn(noise, prediction)
   # Update training metric.
   val_acc_metric.update_state(noise,prediction)
   return loss_value

from tqdm.notebook import trange
import time
for e in trange(num_epochs): 
   print("\nStart of epoch %d" % (e,))
   start_time = time.time()
   
   # this is cool utility in Tensorflow that will create a nice looking progress bar
   for i, batch in enumerate(iter(train_generator)):
       # run the training loop
       loss = train_step(batch)

    # Display metrics at the end of each epoch.
   train_acc = train_acc_metric.result()

   print("Training MSE: %.4f" % (float(train_acc),))
   # Reset training metrics at the end of each epoch
   train_acc_metric.reset_states()
   
   for i, batch in enumerate(iter(val_generator)):
       # run the training loop
       val_loss = test_step(batch)
   val_acc = val_acc_metric.result()
   val_acc_metric.reset_states()
       
   print("Validation MSE: %.4f" % (float(val_acc),))
   # print("validation KID: %.4f" % (float(val_kid),))
   print("Time taken: %.2fs" % (time.time() - start_time))
   
   ckpt_manager.save(checkpoint_number=e)

2.6 Get sample (khuyến tán ngược)

Quá trình lấy mẫu như trong bảng thứ hai của hình * và dựa trên phương trình(16):

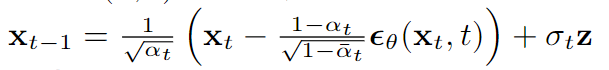
def ddpm(x_t, pred_noise, t):
   alpha_t = np.take(alpha, t)
   alpha_t_bar = np.take(alpha_bar, t)

   eps_coef = (1 - alpha_t) / (1 - alpha_t_bar) ** .5
   mean = (1 / (alpha_t ** .5)) * (x_t - eps_coef * pred_noise)

   var = np.take(beta, t) 
   z = np.random.normal(size=x_t.shape)

   return mean + (var ** .5) * z

2.7 Hiển thị thông tin quá trình khuyến tán

from PIL import Image
def save_gif(img_list, path="", interval=500):
    # Transform images from [-1,1] to [0, 255]
    imgs = []
    for im in img_list:
        im = np.array(im)
        im = (im + 1) * 127.5
        im = np.clip(im, 0, 255).astype(np.int32)
        im = Image.fromarray(im) 
        imgs.append(im)
    
    imgs = iter(imgs)

    # Extract first image from iterator
    img = next(imgs)

    # Append the other images and save as GIF
    img.save(fp=path, format='GIF', append_images=imgs,
             save_all=True, duration=interval, loop=0)
             
from tqdm import tqdm
x = tf.random.normal((1,32,32,1))
img_list = []
img_list.append(np.squeeze(np.squeeze(x, 0),-1))
for i in tqdm(range(timesteps)):
    t = np.expand_dims(np.array(timesteps-i, np.int32), 0)  
    pred_noise = net(x, t)
    x = ddpm(x, pred_noise, t)
    
    img_list.append(np.squeeze(np.squeeze(x, 0),-1))
    if i % 25==0:
        img = np.squeeze(x[0])
        plt.imshow(np.array(np.clip((img + 1) * 127.5, 0, 255), np.uint8))
        plt.show()
save_gif(img_list + ([img_list[-1]] * 100), "ddpm.gif", interval=20)
plt.imshow(np.array(np.clip(img,a_min=0, a_max=255)))
plt.show()

Ảnh của mình sau khi generator.

3. Tổng Kết

Vậy là kết thúc phần series thứ 3 , nếu có bất cứ thắc mắc vui lòng đặt comment bên phía dưới mình sẽ giải đáp . Tuy nhiện DDPM có rất nhiều yếu điểm diffussion model có rất nhiều các giải pháp đã khắc phục nhược điểm đó nhưng hãy để mọi thứ trong series sau.

Tham khảo.

https://medium.com/@vedantjumle/image-generation-with-diffusion-models-using-keras-and-tensorflow-9f60aae72ac
https://arxiv.org/abs/2006.11239

Cảm ơn tất cả mọi người đã theo dõi . Chúc mọi người vui vẻ 😅😅😅😅😅😅😅😅😅