1 . Giới thiệu về sơ lược về diffusion model

Trong bài viết này mình sẽ giới thiệu sơ qua về mô hình và ứng dụng của chúng quan trọng hơn hết với những thành công của mô hình diffussion hiện nay về các lĩnh vực Text2Img . Chúng đang trở nên rất phổ biến khi được giới thiệu và chú ý đến từ cuối năm 2021 đến năm nay.

Đáng chú ý là với các mô hình nổi tiếng hiện nay như stable diffusion hay Dall-e và nổi bật nhất là phần mền mjourney đã tạo nên nhiều kỳ tích trong lĩnh vực vẽ tranh . Có thể nói Text2Img đáng là chủ đề hót nhất hiện nay của mọi paper . Trong bài báo này chúng ta sẽ cố gắng hiểu chi tiết về hộp đen đằng sau chúng.

Trong quá khứ 2 mô hình sinh là VAE và GAN đã thống trị rất rất lâu , hơn hết là GAN . Mặc dù GAN hoạt động tốt với rất nhiều các ứng dụng khác nhau tuy nhiên rất khó để đào tạo do bị ván đề vanishing gradients tức khi đào tạo mạng lớn và khi backward gradient triệt tiêu khiến chúng rất nhỏ rồi nhân với nhau càng nhỏ hơn nên các parameter khó có thể học được thông tin và không thể cập nhật chính xác.Hơn nữa đầu ra ảnh của GAN sẽ thiếu đi tính đa dạng phong phú. bạn có thể hiểu để tạo ra một hình ảnh đa dạng độc đáo và phong phú nội dung GAN không phải là một giải pháp hơn nữa

Khái niệm chính trong Mô hình Diffussion là nếu chúng ta có thể xây dựng một mô hình học tập có thể tìm hiểu sự phân rã có hệ thống của thông tin do nhiễu, thì có thể đảo ngược quá trình và do đó, khôi phục thông tin trở lại từ nhiễu. Khái niệm này tương tự như VAE ở chỗ nó cố gắng tối ưu hóa một hàm mục tiêu bằng cách chiếu dữ liệu vào không gian tiềm ẩn trước tiên và sau đó khôi phục dữ liệu trở lại trạng thái ban đầu. Tuy nhiên, thay vì học cách phân phối dữ liệu, hệ thống hướng tới việc lập mô hình một loạt các phân phối nhiễu trong Chuỗi Markov và “giải mã” dữ liệu bằng cách hoàn tác / làm thay đổi dữ liệu theo kiểu phân cấp.

2. Nền tảng

Người đọc phải có nền tảng về các mô hình sinh cơ bản như hàm loss ELBO, VAE và Hierarchical VAE.

Hình 1: Mô tả quá trình hoạt động diffussion model

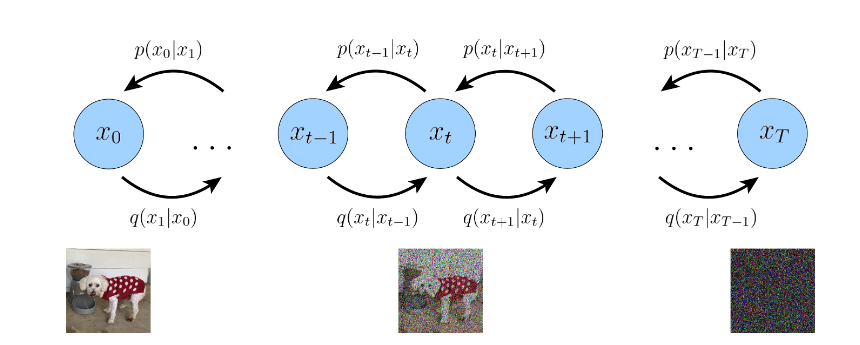
Nhìn vào hình ảnh ta có thể nhận ra diffusion model tìm cách làm nhiễu (noise) các ảnh theo T bước thời gian . T ảnh cuối cùng là một Gaussion tiêu chuẩn với $N(0,I)$ tức là một ảnh nhiễu hoàn toàn không có thông tin chính xác .

Nhắc lại về VAE thì ta có thể hiểu rằng chúng cố gắng hoàn toàn tạo ảnh dựa khả năng tái tạo của ảnh (ELBO) và KL ( đo khoảng cách giữa hai phân phối biến tiềm ẩn z tạo ra từ giá trị dự đóan và ảnh giá trị gốc)

Chúng ta sẽ nhắc lại chút về ELBO,VAE,và Hierarchical để các bạn có thể nắm rõ hơn chi tiết về chúng như vậy chúng ta cũng có thể hiểu rõ hơn về diffussion model . Do bài viết này cực kỳ dài nên mình sẽ cố gắng đến những đoạn quan trọng nhất.

2.1 ELBO

Ở đây chúng ta sẽ cố gắng quan sát được các biến tiềm ẩn z và dữ liệu x input là mật độ phân phối $p(x,z)$ .

Hình 2: Mô tả quá trình hoạt động VAE

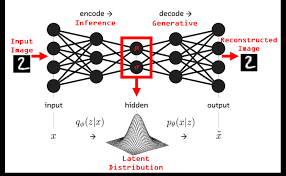
Nhớ lại rằng chúng ta sẽ cố gắng tối ưu hóa output $x$ tiệm cận với tất cả quan sát input $x$ . Hay còn gọi là "likehood-based" . Tìm cách tính xác suất cao nhất của output x dựa trên quan sát x và biến tiềm ẩn z. Lưu ý về VAE biếm tiềm ẩn z luôn có chiều hay số lượng nút ẩn bé hơn đầu vào và ra của dữ liệu. Chúng ta sẽ viết ngắn gọn bới toán học với công thức mô tả $p(x)$, phương trình số (1)

$$p(x)= \int p(x,z)dz$$

Hoặc chúng ta có thể viết lại như sau dựa trên quy tắc chuỗi xác suất:

$$P(X,Y) = P(X|Y). P(Y)$$

$$P(Y) = P(X,Y)/ P(X|Y)$$

Suy ra , phương trình số (2)

$$p(x) = \frac{p(x,z)}{p(z|x)}$$

Tuy nhiên việc tính toán và tối ưu hóa $p(x)$ dựa trên phương trình (1) là rất khó vì ta phải tính cả biến tiềm ẩn z , hơn nữa cũng vì vậy mà phương trình (2) ta không có cách để tính $p(z|x)$ . Tuy nhiên nếu ta kết hợp cả hai chúng lại với nhau ta sẽ được ELBO tối đã hóa khả năng tái tạo của output x dựa trên input x và biến tiềm ẩn z. Khi đó việc tối đa hóa khả năng xảy ra của ELBO sẽ là tối ưu hóa mô hình luôn.

Để “lượng hoá” lượng thông tin này thành số lượng bit, Shannon đề xuất một hàm “lượng tin”, hay sẽ chủ yếu đề cập đến với tên entropy, nhằm tính toán số “bit” thông tin nhận được ứng với một (nhóm) sự kiện nào đó.

$$I ( X ) = - \log _ { 2 } p ( X )$$

Từ đó ta có thể viết ELBO , phương trình số (3) như sau , như trên hình vẽ ta không thể tính được $p(z|x)$ tuy nhiên việc tính toán encoder $q_{\phi}(z|x)$ thì hoàn toàn có thể lưu ý sẽ có parameter ${\phi}$.

$$\log p ( x ) \geq E _ { q _ {\phi} ( z | x ) } [ \log \frac { p ( x , z ) } { q _ {\phi } ( z | x ) } ]$$

Ở đây, $q_{\phi}(z|x)$ có tham số ${\phi}$ mà chúng tôi tìm cách tối ưu hóa. Chúng ta sẽ học cách tham số hóa ${\phi}$ sao cho tính gần đúng $p (z | x)$. Chúng ta sẽ điều chỉnh cập nhật các ${\phi}$ để tối ưu hóa khả năng ELBO khi đó ta sẽ có được mô hình sinh có ảnh dự đoán giống với đầu vào x . Bây giờ chúng ta sẽ tìm cách tối ưu hóa ELBO để hiểu tại sao ta cần tối ưu hóa chúng, chứng minh phương trình số (3) Từ phương trình số (1) ta có:

(4)

$$p(x)= \int p(x,z).1dz$$

(5)

$$= \log \int \frac { p ( x , z ) q _ { \phi } ( z | x ) } { q _ { \phi } ( z | x ) } d z$$

mà (6)

$$1 =\frac{q_{\phi}(z|x)}{q_{\phi}(z|x)}$$

Từ định nghĩa của kỳ vọng

$$E ( x ) = \int x p ( x ) d x$$

$$= \log \int \frac { p ( x , z )} {q _ { \phi } ( z | x ) } { q _ { \phi } ( z | x ) } d z$$

suy ra , phương trình sô (7) từ định nghĩa của kỳ vọng

$$= \log E _ { q_\phi } ( z | x ) [ \frac { p ( x , z ) } { q _ { \phi} ( z | x ) } ]$$

Áp dụng bất đẳng thức jense, phương trình số (8)-ELBO:

$$\geq E _ { q _ {\phi } ( z | z ) } [ \log \frac { p ( x , z ) } { q _ { \phi } ( z | x ) } ]$$

$\text{BDT jense áp dụng với hàm lồi với quy tắc }\ F(E[x]) >= E[F(x)]$

Hình 3: Chứng minh ngắn gọn đằng sau BĐT (bất đẳng thức)

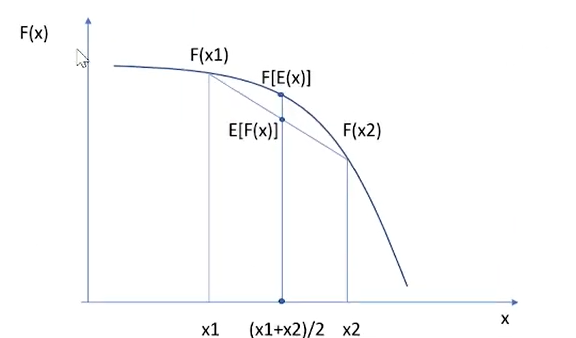
Nhìn vào hĩnh vẽ ta thấy ngay các bạn cũng có thể thử với $F(x)$ và $x$ bất kỳ thì chúng luôn tồn tại quy luật như vậy. Từ phương trình số (7) ta sử dụng BDT jense nhưng chúng ta chưa thực sự hiểu rõ chi tiết tại sao ELBO lại là mục tiêu tối ưu hóa khả năng xảy ra khi sinh ra ảnh vì vậy ta dựa trên phương trình số (2) ta có:

(9)

$$\log p ( x ) = \log p ( x )$$

(10)

$$\log p ( x ) = \int \log p ( x )q _ { \phi } ( z | x ) d z$$

Do

$$\int q _ { \phi } ( z | x ) d z = 1$$

(11)

$$=E _ { q_ { \phi} ( z | x ) } [ \log p ( x ) ]$$

Áp dụng phương trình số (2) ta có được (11)

$$= E _ { q_ { \phi} ( z | x ) }[ \log \frac { p ( x , z ) } { p ( z | x ) } ]$$

(12)

$$= E _ { q_ { \phi} ( z | x ) }[ \log \frac { p ( x , z ) { q_ { \phi} ( z | x ) }} { p ( z | x ){ q_ { \phi} ( z | x ) } } ]$$

(*)

$\text{Bảng công thức logarit}\ { \log _ { a } b + \log _ { a } c } { = \log _ { a } ( b . c ) } \text{ và }$

$${E[X+Y] = \int^∞_{-∞}\int^∞_{-∞}}$$

$$= \int^∞_{-∞}\int^∞_{-∞}xf(x,y)dydx + \int^∞_{-∞}\int^∞_{-∞}yf(x,y)dxdy$$

$$= \int^∞_{-∞}xf_X(x)dx + \int^∞_{-∞}yf_Y(y)dy$$

$$= E[X] + E[Y]$$

(13)

$$= E _ { q _ {\phi } \left ( z | x \right ) } \left [ \log \frac { p \left ( x , z \right ) } { q _ {\phi } \left ( z | x \right ) } \right ] + E _ { q _ {\phi } \left ( z | x \right ) } \left [ \log \frac { q _ {\phi } \left ( z | x \right ) } { p \left ( z | x \right ) } \right ]$$

(14) Định nghĩa KL

Nói cách khác đó là sự khác biệt giữa logarit $P$ và $Q$.trong đó kỳ vọng được thực hiện bằng cách sử dụng các xác suất $P$..

$$= E _ { q _ {\phi } } ( z | x) \left [ \log \frac { p \left ( x , z \right ) } { q _ {\phi } \left ( z | x \right ) } \right ]+ D _ { K L } ( q _ { \phi } ( z | x ) \| p ( z | x ) )$$

(15) Do KL luôn >=0

$$\geq E _ { q _ {\phi } } ( z | x)\left [ \log \frac { p \left ( x , z \right ) } { q _ {\phi } \left ( z | x \right ) } \right ]$$

Từ phương trình số 14 ta có thể rút ra hai kết luận về ELBO

1. ELBO luôn là giới hạn dưới và chúng sẽ kết hợp với Kl để có khả năng ước tính tốt nhất ảnh tạo ra mục tiêu maximun chúng
2. Kl là khoảng cách phân phối giữa $p(x,z)$ với $q_{\phi} (z|x)$ điều kiện tốt nhất là bằng 0 tức minimun chúng . Tối ưu hóa tham sô ${\phi}$ sao cho $q_{\phi} (z|x)$ và $p(x,z)$ bằng nhau nhưng rất khó vì ta không thể truy cập vào $p(z|x)$ nên ta có thể biết rằng càng tối ưu hóa ELBO thì càng gần với ảnh gốc , ảnh tạo ra cũng sẽ đạt tiệm cận ảnh gốc

2.2 VAE

Mình cũng không ngờ viết bằng latex khó và dài nữa , mong mọi người ủng hộ mình . Ở đây chúng ta sẽ đào sâu hơn tiếp vào ELBO dựa trên phương trình (15)

(16)

$$E _ { q \phi \left ( z | z \right ) } \left [ \log \frac { p \left ( x , z \right ) } { q _ { \phi } \left ( z | x \right ) } \right ] = E _ { q \phi \left ( z | z \right ) } \left [ \log \frac { p _ { \theta } \left ( x | z \right ) p \left ( z \right ) } { q _ { \phi } \left ( z | x \right ) } \right ]$$

$\text{Lưu ý rằng là quy tắc chuỗi xác suất}\ P(x,z) = P(x|z).p(z)$

Dựa trên (*)

(17)

$$E _ { q _ { \phi } ( z | x ) } [ \log p _ { \theta } ( x | z ) ] + E _ { q _ { \phi } ( z | x ) } [ \log \frac { p ( z ) } { q _ { \phi } ( z | x ) } ]$$

(18) Định nghĩa KL

$$= E _ { q _ { \phi } ( z | x ) } [ \log p _ { \theta } ( x | z ) ] - D _ { K L } ( q _ { \phi } ( z | x ) \| p ( z ) )$$

$$= E _ { q _ { \phi } ( z | x ) } [ \log p _ { \theta } ( x | z ) ] - 0 . 5 * \sum _ { i = 1 } ^ { N } 1 + \log \left ( z _ { \sigma _ { i } } ^ { 2 } \right ) - z _ { \mu _ { i } } ^ { 2 } - z _ { \sigma _ { i } } ^ { 2 }$$

Trong phương trình (18) có 2 đoạn doạn 1 tiếng anh gọi là reconstruction term đoạn 2 gọi là prior matching term . ở đoạn 1 ${p_{\theta}(x|z)}$ với tham số ${_\theta}$ chuyển các biến tiềm ẩn z thành ảnh dự đoán chúng ta có gọi là decoder. ở đoạn 2 ${q_{\phi}(z|x)}$ với tham số ${_\phi}$ là chuyển đầu vào thành các tiềm ẩn z chúng ta gọi là encoder.

Đoạn 1 reconstruction term đo lường khả năng tái tạo ảnh từ biến tiềm ẩn z cố gắng tối ưu hóa max để tiệm cần sao cho giống ảnh gốc nhất có thể Đoạn 2 đo lương khoảng cách 2 phân phối tạo biến tiềm ẩn z từ đầu vào encoder so với tiềm ẩn gốc . Để ý tiềm ẩn gốc p(z) (gaussian tiêu chuẩn) là có sẵn không có tham số ta cần tối đa hóa min

Từ đó ta có thể nhận ra rằng có 2 tham số ${_\theta}$ và ${_\phi}$ và hơn hết bộ encoder được tham số với ${_\phi}$ , decoder là ${_\theta}$ . Bộ encoder của VAE dựa trên phân phối đa biến Gaussian với hiệp phương sai đường chéo hay ta có thể viết.

(19) Normal với trung bình u và độ lệch chuẩn

$$q _ { \phi } ( z | x ) = N ( z ; \mu _ { \phi } ( x ) , \sigma _ { \phi } ^ { 2 } ( x ) I )$$

(20) Gaussian tiêu chuẩn với trung bình = 0 và độ lệch chuẩn là 1

$$p ( z ) = N ( z ; 0 , I )$$

Tiếp theo chúng ta sẽ tạo ra biến tiềm ẩn z từ trung bình mẫu và độ lệch chuẩn đôi lúc gọi là kỹ vọng và phương sai, lưu ý rằng trung bình mẫu có tham số phi và độ lệch chuẩn cũng vậy . Giải pháp là reparameter trick hay còn gọi là thủ thuật reparameter. Thủ thuật reparameterization viết lại một biến ngẫu nhiên như một hàm xác định của một biến noise; điều này cho phép optimizer các thuật ngữ không ngẫu nhiên thông qua gradient. Ví dụ: các mẫu từ phân phối ${q_{\phi}(z|x)}$ với tham số ${\phi}$ viết lại thành. (21)

$$z = \mu _ { \phi } ( x ) + \sigma _ { \phi } ( x ) \odot \epsilon \quad \text { w i t h } \epsilon \sim N ( \epsilon ; 0 , I )$$

Do đó ta có thể hiểu phần encoder sẽ tối ưu hóa $\mu _ { \phi } ( x )$ với tham số ${\phi}$ và $\sigma _ { \phi } ( x )$ cũng với tham số ${\phi}$. Sau khi bạn train VAE qua encoder tạo ra tiềm ẩn z việc tạo ra ảnh mới sẽ thông qua bộ giải mã với tham số theta . ở đây phần decoder với tham số theta sẽ thông qua $P(x|z)$ hay là khoảng cách mse giữa ảnh đào tạo và ảnh gốc.

2.3 Hierarchical Variational Autoencoders

Chúng ta sắp xong series 1 và mình nhận thấy rằng không đủ thời gian để gói gọn diffussion model trong một bài viết nên mình sẽ chia làm nhiều series để mọi người có thể hiểu và phần này là phần rất quan trọng . Có thể hiểu mô hình này vẫn là VAE nhưng sử dụng nhiều biến tiềm ẩn hơn bạn đừng nhầm lẫn số nút ẩn mà là số lượng tiềm ẩn thay vì 1 giống như vae ta có thể có rất nhiều tiềm ẩn z . Theo như ta có thể hiểu chúng nhiều như vây.

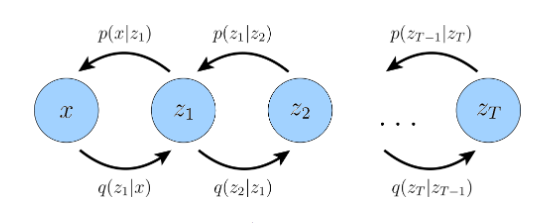
Ta có thể hiểu x là đầu vào và $z_{t}$ là biếm tiền ẩn, $z_{t+1}$ là biến tiềm ẩn tiếp theo và $Z_{T}$ là ảnh dự đoán từ bộ decoder. Nhìn vào ảnh ta có đoán ra ngay encoder sẽ được viết là:

$$q _ { \phi } ( z _ { 1 } | x )(q _ { \phi } ( z _ { 2 } | z_{1} )(q _ { \phi } ( z _ { 3 } | z_{2} )....(q _ { \phi } ( z _ { T } | z_{T-1} )$$

nếu bạn để ý chúng chính là chuỗi markovian và nếu bạn đã quen thuộc với markovian thì có thể viết lại thành

(22)

$$q _ { \phi } ( z _ { 1 } | x ) \prod _ { t = 2 } ^ { T } q _ { \phi } ( z _ { t } | z _ { t - 1 } )$$

Sau khi đã xong encoder chúng ta sẽ tiếp tục với decoder:

$$p ( z _ { T } ) p _ { \theta } ( x | z _ { 1 } )p _ { \theta } ( z_{1} | z _ { 2 } )p _ { \theta } ( z_{2} | z _ { 3 } ).........(p _ { \theta } ( z _ { T-1 } | z_{T} )$$

viết lại đơn giản thành.

(23)

$$p ( z _ { T } ) p _ { \theta } ( x | z _ { 1 } ) \prod _ { t = 2 } ^ { T } p _ { \theta } ( z _ { t - 1 } | z _ { t } )$$

Từ (22) và (23) và áp dụng phương trình số (8) ta có:

$$E _ { q _ { \phi } ( z _ { 1 } | x ) \prod _ { t = 2 } ^ { T } q _ { \phi } ( z _ { t } | z _ { t - 1 } ) } [ \log \frac { p ( z _ { T } ) p _ { \theta } ( x | z _ { 1 } ) \prod _ { t = 2 } ^ { T } p _ { \theta } ( z _ { t - 1 } | z _ { t } ) } { q _ { \phi } ( z _ { 1 } | x ) \prod _ { t = 2 } ^ { T} q _ { \phi } ( z _ { t } | z _ { t - 1 } ) } ]$$

2.4 Kết luận

Qua series này các bạn đã hiểu chi tiết đằng sau hàm loss autoencoder và variable autoencoder chúng ta có 2 tham số cần tối ưu với encoder là phi và với decoder là theta . Hàm loss có 2 đoan chính đoạn 2 chính là khoảng cách phân phối giữa tiềm ẩn tạo ra và tiềm ẩn gaussian tiêu chuẩn , đoạn 1 chính là khả năng tái tạo của ảnh so với ảnh ban đầu được tối ưu hóa bằng tham số theta hay còn gọi là ELBO. Mình sẽ làm tiếp series 2 và 3 phần series 3 sẽ nói nhiều hơn về nhiệt động lực học , series 2 là diffussion model . và còn rất nhiều các thể loại diffussion khác nhau chúng ta sẽ tìm hiểu thêm về chúng nữa . Rất mong được các bạn ủng hộ.

~~Tài liệu tham khảo ~~

https://arxiv.org/pdf/2208.11970v1.pdf

https://paperswithcode.com/paper/nvae-a-deep-hierarchical-variational

https://viblo.asia/p/tan-man-ve-generative-models-part-1-cac-mo-hinh-autoencoder-vaes-4P856rw35Y3 😄😄😄😄😄😄