Chúng ta sẽ bắt đầu tuần 4 của xử lý ảnh, mình học xử lý ảnh từ kì 1 trước, giờ không nhớ gì nhiều :v giờ đọc lại và viết lại để có thể nhớ vậy.

Chúng ta sẽ nhắc lại kiến thức về bài viết trước bao gồm:

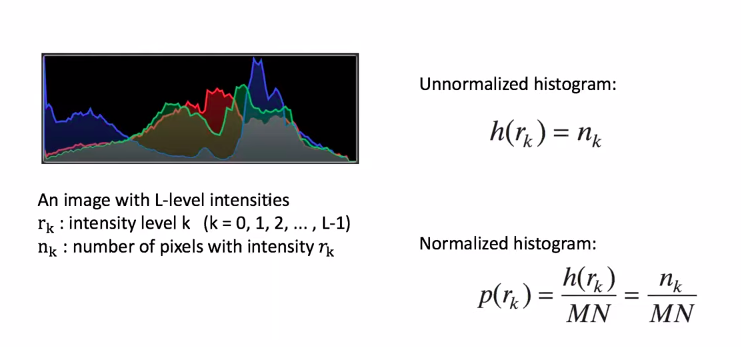
• về histogram là biểu đồ về độ phân chia của mức sáng:

• Histogram cũng phản ánh hiện trạng của ảnh như thế nào? ví dụ như tối quá, sáng quá,...

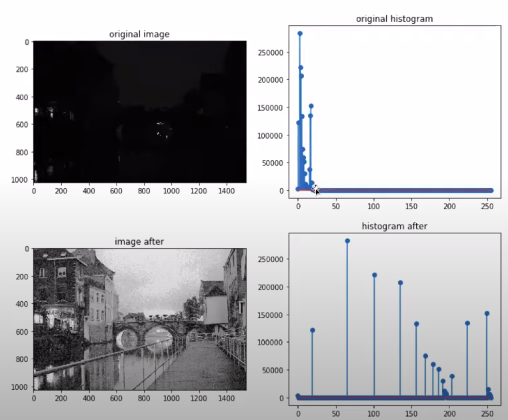
• Cân bằng biểu đồ mức xám ( Histogram Equalization)

Như các bài viết trước, chúng ta chỉ quan tâm đến điểm ảnh , từ bài này trở đi chúng ta sẽ quan tâm đến cả các điểm ảnh bên cạnh điểm ảnh đó. Trong bài viết này, chúng ta sẽ tìm hiểu phép lọc trong không gian điểm ảnh. Trước hết ta có một số định nghĩa.

Định nghĩa

Neighbors of a pixel

Có nhiều định nghĩa về lân cận của một điểm ảnh, hay dùng nhất là 4 - neighbors, 8 - neighbors như hình dưới.

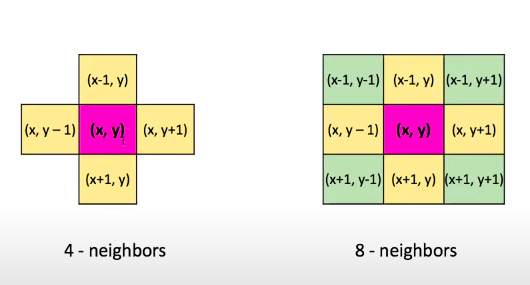
Nhưng nếu ta muốn định nghĩa về các điểm lận cận xa hơn điểm (x,y) thì làm như thế nào ?. Vì vậy, ta có thêm định nhĩa mới là khoảng cách giữa 2 điểm ảnh.

Distance between two pixels

Ta có 2 pixel p = (x,y) và y = (u,v)

Khoảng cách giữa 2 pixcel ta có dùng công thức Euclidean:

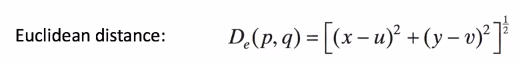
Nhưng kết quả đầu ra có thể là một số không nguyên, không dùng được trong định nghĩa lân cận giữa các điểm. Vì thế, ta dùng công thức City-block hay còn gọi là công thức Manhattan đơn giản hơn kêt quả sẽ ra là số nguyên.

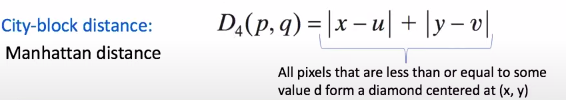
Áp dụng có nó trong định nghĩa về lân cận như sau:

Điều khó khăn khi áp dụng công thức này là để biểu diễu cấu trúc các điểm lân cận này ví nó có hình dạng là hình thoi. Nếu biểu diễn thì cần là ma trận hình vuông hoặc hình chữ nhật với nhiều số 0 ở các góc và như vậy sẽ thừa tài nguyên. Ví vậy ta nghĩ đến công thức tính khoảng cách mới.

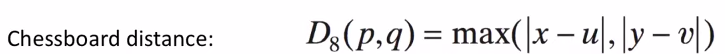
Các ví dụ về định nghĩa các điểm lận cận với công thức này:

Spatical filter kernel

Hay còn có nhiều cái tên gọi khác là mask, template, window, filter, kernel. Nó chỉ chung là một matrix mà kích thước của nó định nghĩa lân cận của phép toán mà mình áp dụng và giá trị của từng phần tử thể hiện bản chất của filter.

Spatical filter sẽ thay đổi ảnh bằng cách thay thế giá trị của từng pixel bởi một hàm của điểm ảnh và các điểm lân cận của nó.

Linear spatial filtering mechanism (cơ chế biến đổi tuyến tính)

Biến đổi ảnh tuyến tính thực hiện thao tác tính tổng các tích giữa hình ảnh f và filter kernel w và thay giá trị điểm ảnh đó bằng giá trị tổng vừa tìm được. Lưu ý rằng vị trí hệ số w(0,0) trùng với vị trí điểm ảnh f(x,y) đang cần biến đổi.

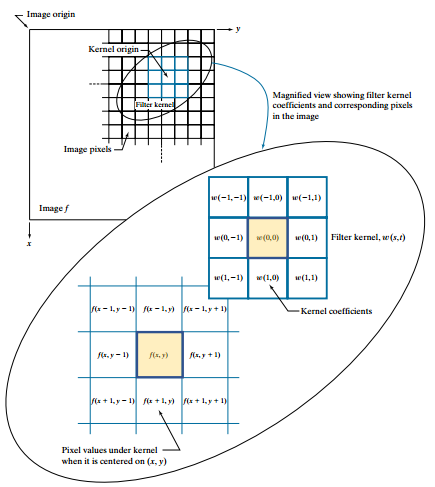
Một cách tổng quát, biến đổi một ảnh $f(x,y)$ có kích thước $M*N$ sử dụng ma trận filter kernel tuyến tính kích thước $m*n (m = 2a + 1, n = 2b+1)$ với a, b là các số không âm được thực hiện bởi công thức:

Như đã giới thiệu ở trên thì ta có phép toán tính tổng các tích, ở trong xử lý ảnh có 2 phép toán có thể làm được như vậy. 1 phép toán là Correlation và phép toán còn lại là convolution. Ta sẽ cùng tìm hiểu và phân biệt nó.

Correlation vs Convolution

Spatial correlation and convolution in 1D

Với 1 chiều thì côgn thức trên sẽ trở thành:

Ở đây, ta ví dụ với một hàm 1-D: $f$ và một kernel $w$ có kích thước 1 x 5 nên a = 2 và b = 0.

Điều đầu tiên chúng tôi nhận thấy là một phần của $w$ nằm ngoài $f$, do đó, tổng không được xác định trong khu vực đó. Một giải pháp cho vấn đề này là pad hàm $f$ với đủ 0 ở hai bên. Nói chung, nếu hạt nhân có kích thước $1 × m$, chúng ta cần $(m - 1) /2$ số ở hai bên của $f$ để xử lý các cấu hình bắt đầu và kết thúc của $w$ đối với $f$. Hình (c) cho thấy một chức năng pad đúng. Hình (c) cho thấy tâm của kernel phải trùng với pixel ta cần sửa ở đây à pixel đầu tiên.

Lưu ý là Zero padding không phải là lựa chọn padding duy nhất, chúng ta sẽ bàn luận chi tiết hơn ở phần sau về chọn cách padding

Trong hình bên trái thực hiện pháp toán Correlation, còn phép toán Convolution thì khác với Correlation ở chỗ ngay bước đầu tiên, thì ta sẽ xoay kernel $w$ 180 độ, còn lại các bước để chạy tính tổng các tích tương tự.

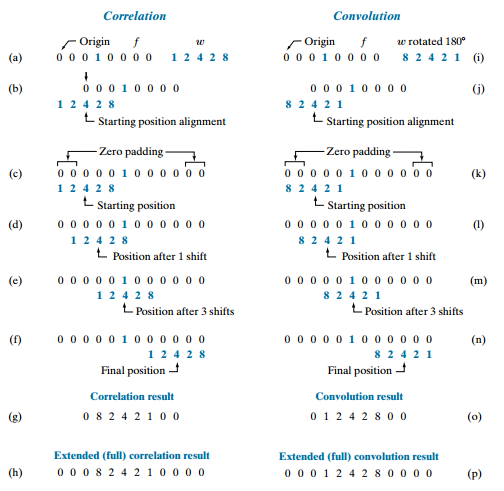
Sau khi thực hiện các phép toán, ta cũng thấy rằng với Correlation, hàm $f$ bị đảo ngược, còn với Convolution thì đâu ra sẽ được giữ nguyên cho ta đúng thứ tự.

Spatial correlation and convolution in 2D

Ở trong 2D ta cũng có kết quả tương tự.

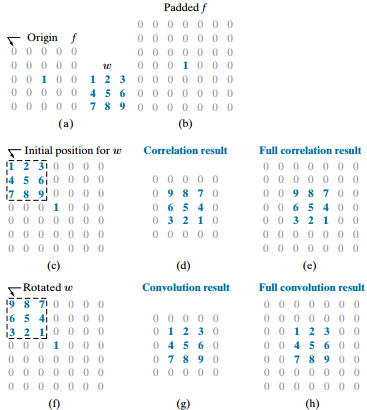
Hầu hết, trong xử lý ảnh sẽ dùng là Convolution, nhưng đối với mạng nơ-ron tích chập gọi là convolutional neural network với phép toán gọi là convolution nhưng bản chất của nó là Correlation

Từ các ví dụ trên ta có công thức toán học cho cả 2 như sau:

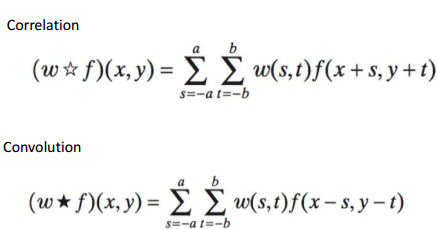
2 công thức chỉ khác nhau dấu + ở trên vào dấu - ở dưới, ví dưới ở dưới sẽ giúp ta hiểu rõ hơn về công thức:

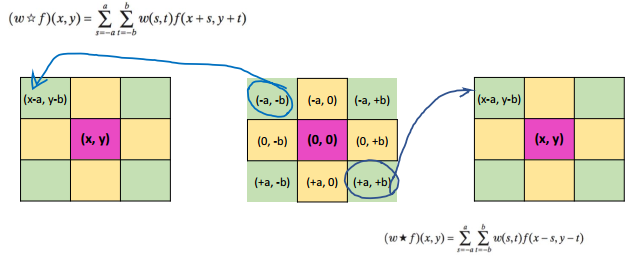
Các tính chất cơ bản của Convolution và Correlation như sau:

Boundary issues

Khi ta làm việc với ảnh làm việc với tích chập, một vấn đề xuất hiện là khi nhân kernel g với ảnh f thì g sẽ bắt đầu nhân với pixel ở ví trị nào ? Có 3 dạng như sau:

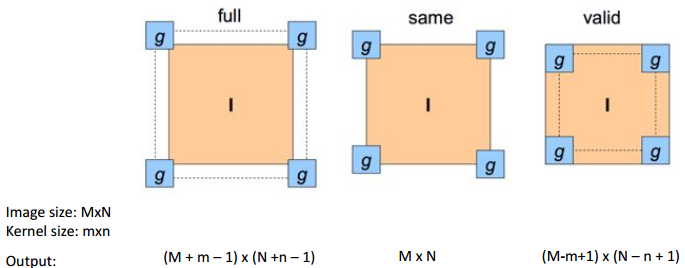
• Kiểu full, kết quả đầu ra của ảnh sẽ có kích thước lớn hơn ảnh gốc. Hình dưới mô tả kiểu full, dưới thì bên trên là ảnh đầu ra và bên dưới là ảnh gốc thêm phân padding là các ô trắng.

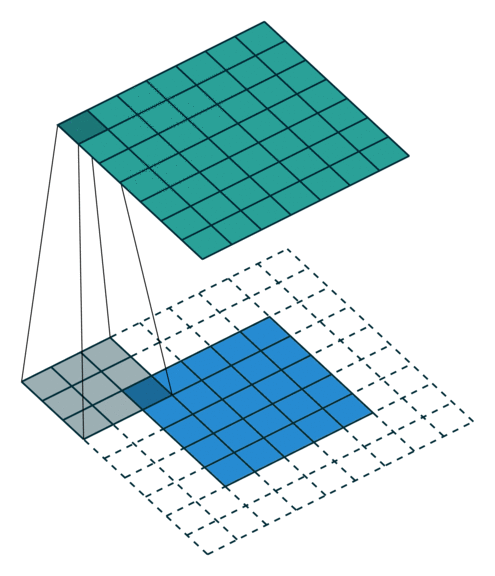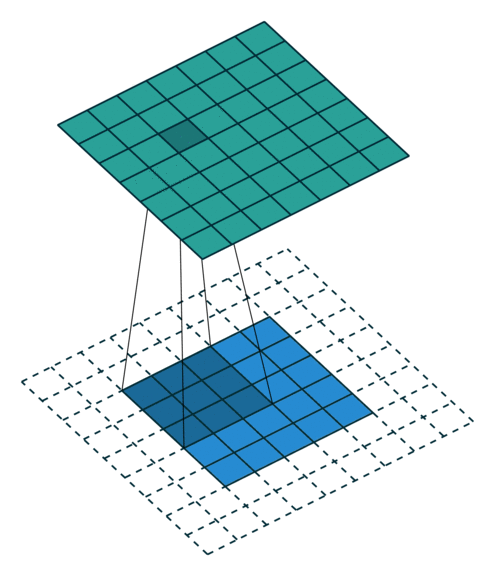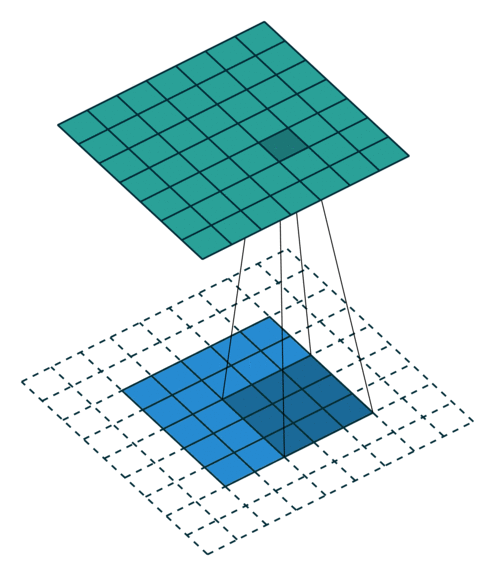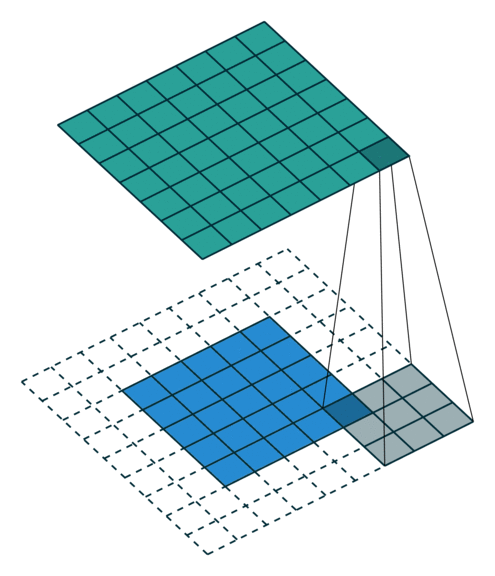
• Kiểu same, kết quả đầu ra của ảnh có kích thước bằng ảnh đầu vào.

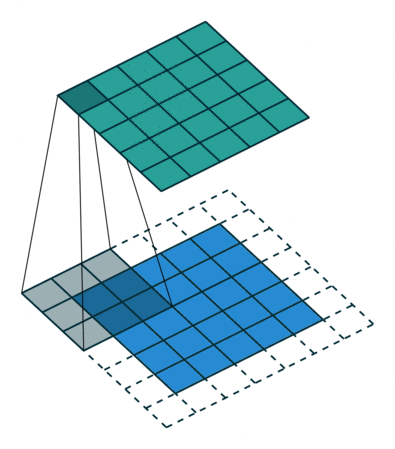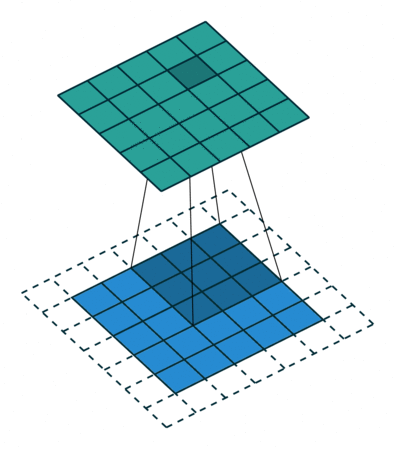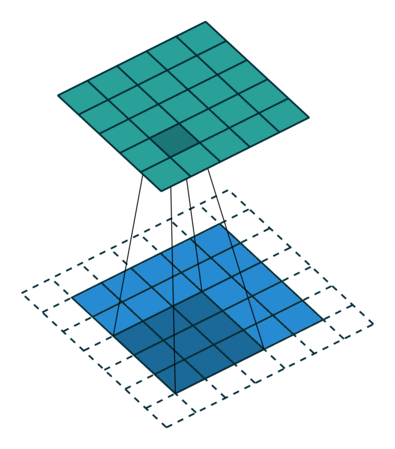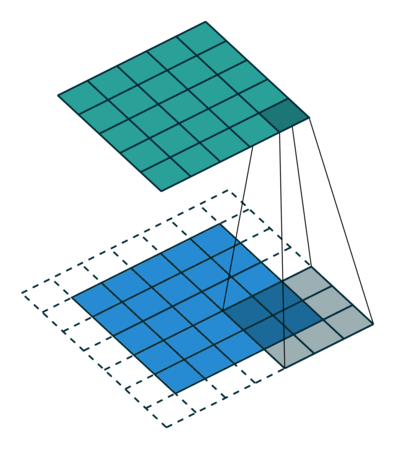
• Kiểu valid, kết quả đầu ra sẽ nhở hơn ảnh đầu vào.

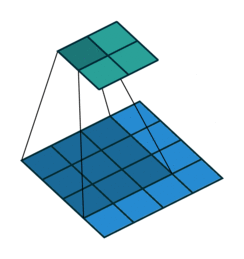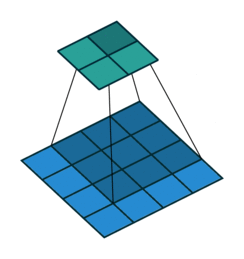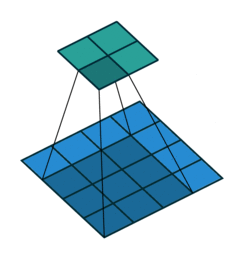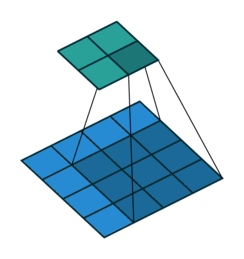
What to do around the borders

Ở kiểu full và valid như ở trên, thì ta cần thêm padding. Vậy ta khởi tạo các padding như thế nào? Thông thường có các loại khởi tạo padding như sau:

• Pad a constant value (black) . Ví dụ phía trên ta cho các padding có giá trị 0 hay còn gọi là zero-padding. Trong opencv sử dụng câu lệnh: cv2.BORDER_CONSTANT
• Wrap around (circulate the image): cv2.BORDER_WRAP
• Copy edge (copy các pixel ở cạnh). Trong opencv, sử dung câu lênh: cv2.BORDER_REPLICATE
• Reflect across edges (đối xứng). Trong opencv, sử dụng câu lệnh: cv2.BORDER_REFLECT

Spatial filter kernels

Filter design

Thiết kế Filter dựa vào một trong các đặc điểm sau:

• Dựa trên các tính chất toán học
  • Ví dụ 1: một bộ lọc tính trung bình các pixel trong vùng lân cận sẽ làm mở ảnh.
  • Ví dụ 2: một bộ lọc tính đạo hàm cục bộ làm sắc nét ảnh.
• Dựa trên việc lấy mẫu một hàm trong không gian 2D mà hình dạng có thuộc tính mong muốn
  • Ví dụ: lấy mẫu từ hàm Gaussian để xây dựng bộ lọc trung bình trọng số
• Dựa trên frequency response ( sẽ học ở tuần Fourier Transform)

Smoothing Filters

• Được sử dụng để giảm chuyển đổi sắc nét về cường độ

  • Giảm chi tiết không liên quan trong ảnh (ví dụ: nhiễu)
  • Làm mịn các đường viền sai do sử dụng không đủ số mức cường độ trong ảnh

• Trong bài viết này, ta sẽ tìm hiểu về các filter kernels sau:

  • Mean filter/Box filter
  • Lowpass Gaussian filter
  • Order-statistic (phi tuyến) filter

Mean filter/Box filter kernels

Ý tưởng đằng sau pháp biến đổi mean filter rất đơn giản. Đó là thay thế giá trị của mỗi điểm ảnh bằng giá trị trung bình của các điểm ảnh lân cận.

Một m x n box filter là một mảng kích thuớc m x n số 1 với hằng số chuẩn hóa ở phái trước có giá trị là 1 chia cho tổng giá trị các hệ số trong mảng ( tức là 1/mn khi tất cả các hệ số đều là 1). Bên dưới ta có 1 ví dụ về box filter kích thước 3 x 3.

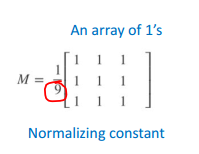
Box filter kernel thường được sử dụng để làm mịn các đường nét hoặc lọc nhiễu nhằm tăng cường chất lượng ảnh. Bên dưới là ví dụ khi ta áp dụng bức ảnh hình a với box filter có kích thước lần lượt là 3 x 3, 11 x 11, 21 x 21. Ta thấy càng tăng kích thước của kernel thì ta thấy ảnh mịn đi và mờ đi.

Gaussian Filter Kernels

Gaussian filter kernels tương tự như box filter kernels nhưng sử dụng các ma trận khác nhau để thể hiện hình dạng của hàm Gaussian và nó được dùng trong bài toán làm mịn và có kết quả tốt hơn box filter kernel.

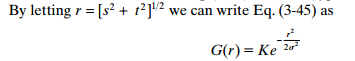
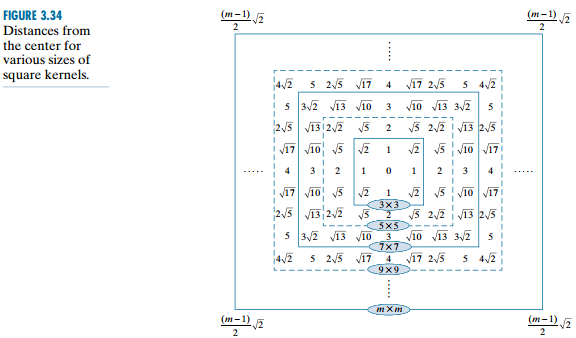
Gía trị r chính là khoảng cách từ tâm đến tất cả các điểm trong hàm G. Ta có thể xem các giá trị của r trong hình dưới.

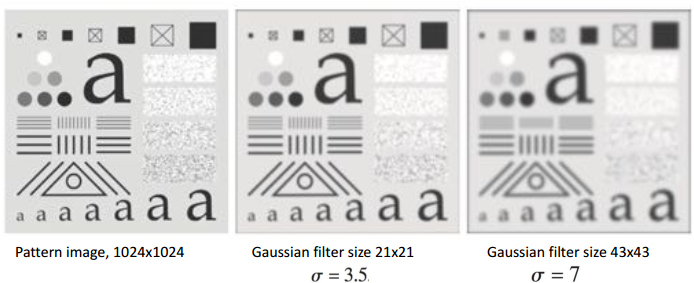
Một số ví dụ sử dụng Gaussian filter với các kích thước và độ lệch chuẩn khác nhau với K = 1 trong tất cả các trường hợp.

So sánh giữa box và Gaussian kernels

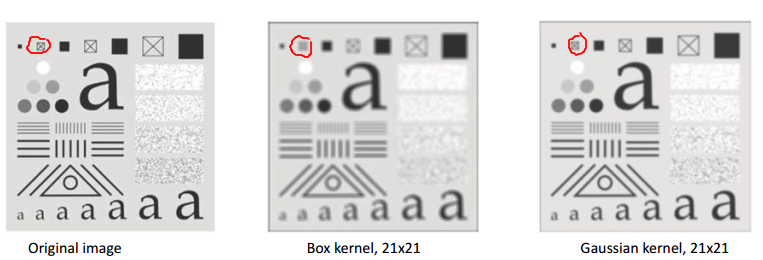
Mọi người để ý vào vùng mình khoang tròn sẽ thấy với kernel cùng kích thước thì box kernel sẽ làm mờ và biến đổi hình dạng của ảnh còn với Gaussian kernel thì chỉ làm mờ. Vì thế trong xử lý ảnh, khi muốn làm mịn ảnh người ta hay dùng Gaussian kernel hơn.

Một ứng dụng khác của Gaussian filters là Shading correction ( chỉnh sửa bóng). Như ví dụ sau:

Order-statistic filters

Đây là bộ lọc không gian phi tuyến tính, không giống như các bộ lọc trên dùng các phép tính cộng trừ nhân chia, bộ lọc này dựa trên thứ tự (xếp hạng) các pixel trong vùng lân cận và sau đó thay thế giá trị của pixel trung tâm bằng giá trị được xác định bởi kết quả xếp hạng.

Các filter được biết tới nhiều nhất là Median filter, một số filter khác thuộc dạng này là Max filter và Min filter.

Median filter

Median filter thay thế giá trị của pixel trung tâm bằng trung vị của các giá trị cường độ trong vùng lân cận của pixel đó. Nó có tác dụng giảm noise tuyệt với trong cac stường hợp như nhiễu ngẫu nhiên hoặc salt-and-pepper noise.

Các bước làm Median filter trong 2D như sau:

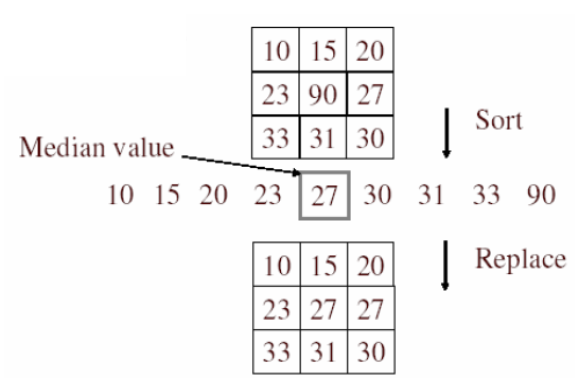
Ví dụ của median filter áp dụng cho một bức ảnh salt-and-pepper noise.

Unsharp masking

Trong phần này, ta sẽ được giới thiệu về filter có tác dụng làm sắc nét các cạnh, cạnh có thể hiểu là chỗ giao chuyển từ mức sáng này sang mức sáng khác. Các bước làm để tạo ra unsharp masking sẽ như hình dưới.

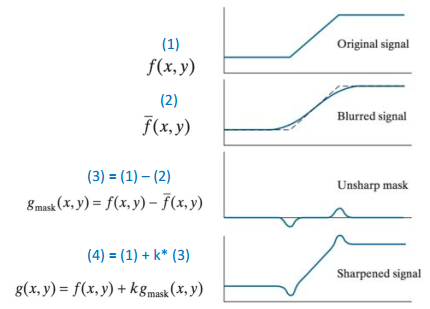
Với k = 1 thì ta gọi g(x,y) là unsharp masking, với k > 1 sẽ được gọi là highbost filtering.

Ta có một ví dụ về unsharp masking để hiểu rõ hơn về các bước làm như sau:

Tổng kết

Bài viết đến đây đã dài, nếu có thắc mắc hoặc góp ý gì cho bài viết của mình để tốt hơn xin vui lòng comment bên dưới. Hẹn gặp lại mọi người trong bài viết tiếp theo của mình.

Tài liệu tham khảo

1. Xử lý ảnh - Lê Thanh Hà
2. R. C. Gonzalez, R. E. Woods, “Digital Image Processing,” 4th edition, Pearson, 2018 Chapter 3.
3. Slide
4. Code github: here
5. http://deeplearning.net/software/theano/tutorial/conv_arithmetic.html
6. Week 4 - Spatial Filtering
7. https://docs.opencv.org/master/d2/de8/group__core__array.html