Xin chào các bạn, hôm nay chúng ta sẽ cùng tìm hiểu về histogram, cân bằng biểu đô mức xám và phân loại ảnh sử dụng histogram.

Ôn lại bài tuần 2

Đâu tiên, chúng ta sẽ điểm qua các kiến thức về phép toán trên điểm ảnh trong bài viết trước.

• Lấy mẫu, lượng tử hóa
• Biến đổi trên điểm ảnh -> chỉnh độ sáng, độ tương phản
  • Gamma
  • Negation
• Kết hợp ảnh
  • Tính trung bình
  • Trừ background

Histogram

1. Khái niệm

Histogram (lược đồ xám) là biểu đồ tần xuất thống kê số lần xuất hiện các mức sáng trong ảnh.

2. Cách tính histogram

• $r_{k}$ là mức xám của ảnh $f(x,y)$
• $n_{k}$ là số điểm ảnh (pixels) có giá trị $r_{k}$
• Biểu đồ mức xám chưa chuẩn hóa (unnormalized histogram) của $f$ được định nghĩa như sau: $h(r_{k}) = n_{k}$ với $k = 0, 1,..., L-1$, $L$ là số mức xám.
• Biểu đồ chuẩn hoá (normalized histogram): $p(r_{k}) = \frac{h(r_{k})}{MN} = \frac{n_{k}}{MN}$ với M, N là chiều dài và chiều rộng của $f$ hay là của ảnh

3. Ví dụ

Ta lần lượt có ảnh và histogram tương ứng với các ảnh drank, light, low-contrast và high-contrast Ta có nhận xét

• Với ảnh dark thì histogram có các cột tập trung vào bên trái tương ứng với màu tối
• Với ảnh light thì histogram có tập trung vào bên phải chứa các pixel trắng
• Với ảnh độ tương phản thấp (low-contrast) thì histogram có các cột tập trung xít nhau và ở giữa
• Với ảnh độ tương phản cao (high-contrast) thì histogram san đều với các giá trị

4. Code

Giả sử ta có bức ảnh độ tương phản như sau: Ta bắt đầu import thư viện và load ảnh.

import numpy as np 
import cv2 
import matplotlib.pyplot as plt

%matplotlib inline
plt.rcParams['figure.figsize'] = [10,8]
img = cv2.imread("low-exposure.jpg", 0)

Chúng ta bắt đầu thử bắt đầu code nào . Ta có 2 cách dùng hàm để tính histogram.

1. Sử dụng cv2.calcHist từ thư viện OpenCV

# using cv2.calcHist()
hist = cv2.calcHist(
      [img],
      channels = [0],
      mask=None, # full image
      histSize=[256], #full scale
      ranges=[0,256]
)
plt.plot(hist)

2. Sử dụng hàm numpy.histogram

#using numpy
h2 = np.histogram(img.ravel(), bins=256, range=[0,256])
print(h2[0].shape)
plt.plot(h2[0])

Và 2 cách trên đều ra kết quả như sau:

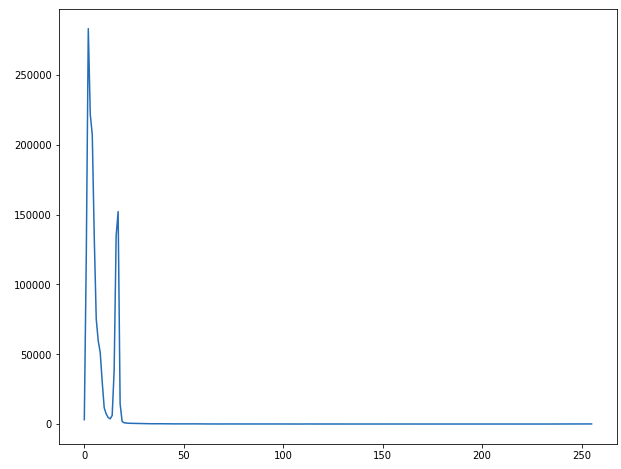
Histogram equalization (cân bằng biểu đồ mức xám)

1. Khái niệm

Phần này là phần mình giới thiệu và chứng minh công thức, nếu thấy quá dài dòng và khó hiểu bạn có thể xem luôn phần các bước làm.

Trong trường hợp ảnh là một hàm liên tục, ta xét biến $r$ đại diện cho các cấp độ xám của ảnh cần được cân bằng và $r$ trong khoảng $[0,L-1]$ với $r = 0$ đại diện cho đen và $r =L-1$ đại điện cho trắng. Cân bằng biểu đồ mức xám là tìm một ánh xạ $s= T(r)$ khi đó mỗi điểm ảnh có giá trị $r$ trong ảnh ban đầu sẽ được ánh xạ tạo nên cấp độ $s$ trong ảnh đẩu ra.

Ta cần tìm hàm $T(r)$ thỏa mãn các điều kiện sau:

1. $T(r)$ là hàm đơn vị và đơn điệu tăng trong khoảng $0\leqslant r \leqslant L -1$
2. $0\leqslant T(r) \leqslant L -1$ với $0\leqslant r \leqslant L -1$

Ở đây ta định nghĩa hàm $p_{r}(r)$ và $p_{s}(s)$ lần lượt biểu diễn hàm mật độ xác suất của các biến ngẫu nhiên $r$ và $s$. Kết quả cơ bản từ lý thuyết xác suất là nếu cho trước $p_r(r)$ và $T(r)$ , $T^{-1}(s)$ thỏa mãi điều kiện 1. thì hàm mật độ xác xuất $p_{s}(s)$ có thể thu được bằng cách sử dụng công thức sau:

Do đó, hàm mật độ xác suất của $s$, được quyết định bởi cấp độ xám PDF của ảnh đầu vào và hàm biến đổi đã chọn. Một hàm biến đổi quan trọng trong xử lý ảnh có dạng:

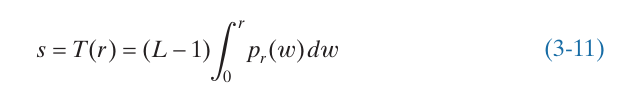
Đẳng thức bên phải của phương trình trên được gọi là hàm phân phối tích lũy của biến ngẫu nhiên $r$, nó đơn điệu tăng thỏa mãn điều kiện 1). Tương tự, tích phân của hàm mật độ xác suất trong khoảng $[0, L-1]$ cũng nằm trong khoảng $[0, L-1]$ nên điều kiện 2 được thỏa mãn. Ta có:

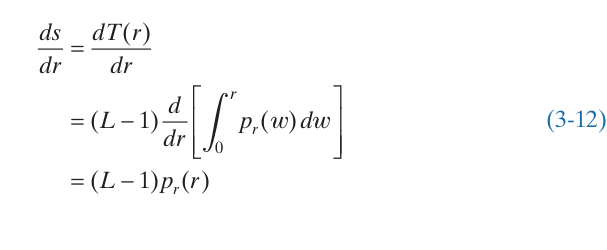
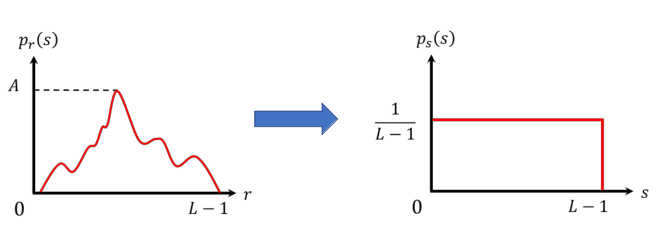
Thay kết quả này cho $\frac{d_{s}}{d_{r}}$ cho phương trình (3 -10), và do tất cả các giá trị xác suất đều dương, ta thu được:

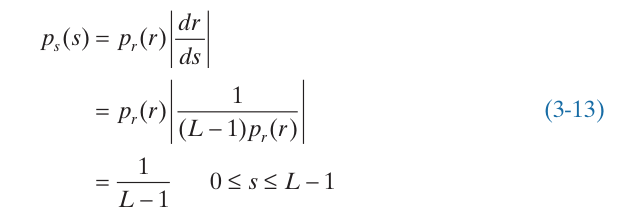
Ta thấy $p_{s}(s)$ là hàm phân bố xác suất đều, từ đó có thể kết luận rằng việc thực hiện phép biến đổi (3-14) đã sinh ra biến ngẫu nhiên $s$ với hàm phân bố xác suất đều.

Khi ảnh là các giá trị độ sáng rời rạc, ta làm việc với xác suất xuất hiện của từng giá trị độ sáng và phép toán tổng xác suất thay vì hàm mật độ xác suất và phép toán tích phân. Xác suất xuất hiện của mức xám $r_{k}$ trong ảnh được tính xấp xỉ bằng $p_{r}(r_{k}) = \frac{n_{k}}{MN}$. Lúc này công thức cho phép biến đổi tương tự trong phương trình (3-10) trên các giá trị rời rạc là:

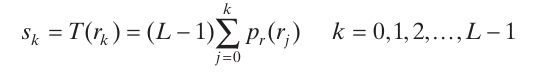
Vậy sau 1 hồi dài dòng để tìm ra công thức , ta có các bước làm.

2. Các bước làm

1. Tính toán histogram $p_{r}(r)$
2. Chuẩn hóa histogram cho về khoảng [0, 1] : $p_{r}(r_{k}) = \frac{n_{k}}{MN}$
3. Tính hàm xác suất mật độ
4. Tính giá trị mức xám cho từng điểm ảnh: O(x, y) = round( T(I(x,y)) )

Ta có ví dụ để cho trực quan hơn. Ta có bảng phân phối cường độ và giá trị histogram cho hình ảnh kỹ thuật số 3 bit ảnh 64 * 64

Theo công thức ta sẽ tính được

L = 8

$s_{0} = T(r_{0}) = 7 * p_{r} (n_{0})=1.33$

Sau đó ta sẽ chuyển đổi giá trị của từng điểm ảnh như sau:

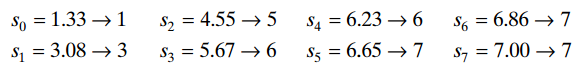
3. Code

Ta sẽ sử dụng bức ảnh bên trên để cân bằng histogram

Cách 1 ta dùng thủ công thì hàm cân bằng histogram như sau:

def hist_equalize(img):
  # 1. calclate hist
  hist = cv2.calcHist([img], [0], None, [256], [0, 256])

  # 2. normalize hist
  h, w = img.shape[:2]
  hist = hist/(h*w)

  # 3. calculate CDF
  cdf = np.cumsum(hist)
  s_k = (255 * cdf - 0.5).astype("uint8")
  return s_k

Tiếp theo ta phải ánh xạ mức xám đầu vào với s_k:

s_k = hist_equalize(img)
equalized_img = cv2.LUT(img, s_k)
plot_img_and_hist(equalized_img)

Cách 2 ta sẽ dùng hàm của OpenCv như sau:

img_equalized = cv2.equalizeHist(img)
plot_img_and_hist(img_equalized)

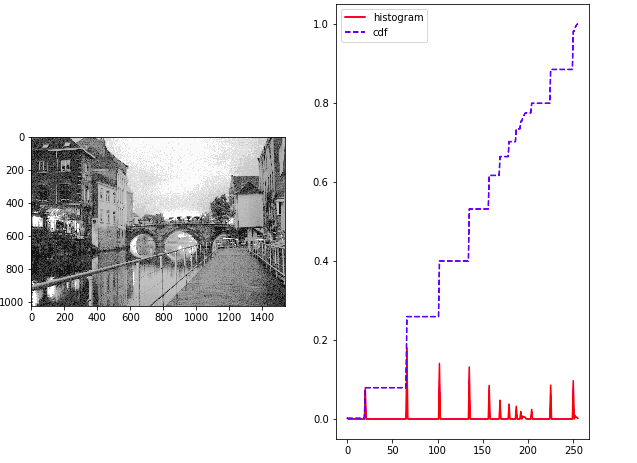
Và kết quả ta sẽ được như sau, bên trai là ảnh đẩu ra và bên phải là histogram và cdf tương ứng.

Tài liệu tham khảo

1. Xử lý ảnh - Lê Thanh Hà
2. R. C. Gonzalez, R. E. Woods, “Digital Image Processing,” 4th edition, Pearson, 2018.
3. Slide
4. Code github: here