vi
new
+3
Avatar
Nguyễn Tiến Đạt @nguyen.tien.datb
1.4K 95 19
Đã đăng vào thg 4 30, 2020 5:04 CH 15 phút đọc
2.0K

Python Numpy Tutorial

Hôm nay mình sẽ giới thiệu cho các bạn về sử dụng thư viện numpy, mục đích một phần cũng để note lại kiến thức cho nhớ và khi nào cần mình có thể vào đây xem lại.😃

Install NumPy

Để cài đặt Python NumPy, cách đơn giản nhất là mở command của bạn và gõ:

pip intall numpy

Sau khi cài đặt kết thúc, khi bạn muốn sử dụng thì bạn khai báo đơn giản như sau:

import numpy as np

Vì numpy là thư viện được sử dụng thường xuyên nên nó thường được khai báo gọn lại như trên np có thể thay thế bằng các từ khác, tuy nhiên bạn nên đặt là np vì các tài liệu hướng dẫn đều ngầm quy ước như thế.

NumPy là gì ?

Theo định nghĩa trên trang chủ của Numpy.

"NumPy is the fundamental package for scientific computing in Python. It is a Python library that provides a multidimensional array object, various derived objects (such as masked arrays and matrices), and an assortment of routines for fast operations on arrays, including mathematical, logical, shape manipulation, sorting, selecting, I/O, discrete Fourier transforms, basic linear algebra, basic statistical operations, random simulation and much more"
-https://docs.scipy.org/doc/numpy-1.10.1/user/whatisnumpy.html.

Bạn có thể hiểu đơn giản: NumPy (Numeric Python) là là thư viện cốt lõi cho tính toán khoa học trong Python. Nó cung cấp một đối tượng mảng đa chiều hiệu suất cao và các công cụ để làm việc với các mảng này.

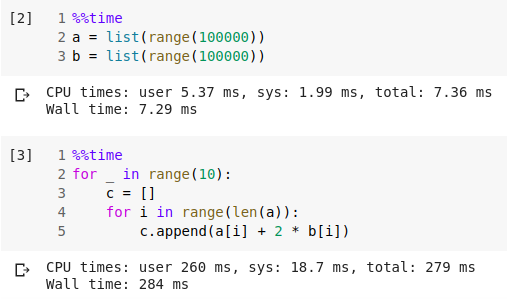
Hãy xem qua một ví dụ cho thấy NumPy mạnh như thế nào. Giả sử chúng ta có hai list a và b, bao gồm 100.000 số không âm đầu tiên và chúng tôi muốn tạo một list mới c có phần tử thứ i là a[i] + 2 * b[i]

Với cách bình thường không dùng NumPy:

Khi dùng NumPy:

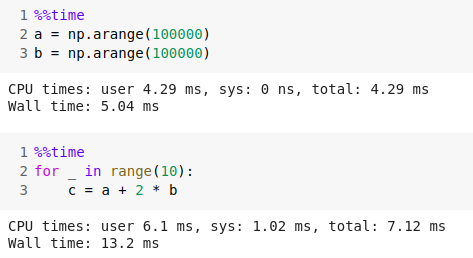
Nhìn vào ta thấy kết quả dùng NumPy nhanh hơn rất nhiều lần và cùng với một mục địch thì ta dùng ít dòng code hơn và bản thân dòng code của chúng ta cũng trực quan hơn.

Python thông thường chậm hơn nhiều do kiểm tra kiểu và chi phí khác cần phải thông dịch mã và hỗ trợ Python's abstractions.

Ví dụ: nếu chúng ta đang thực hiện một số điều kiện trong một vòng lặp, việc liên tục kiểm tra kiểu trong một vòng lặp sẽ dẫn đến nhiều tập lệnh hơn là chỉ thực hiện một thao tác bổ sung thông thường. NumPy, sử dụng tối ưu hóa mã C được biên dịch trước, có thể tránh được rất nhiều chi phí.

Quá trình ta sử dụng ở trên là vectorization. Vectorization đề cập đến việc áp dụng các hoạt động cho các mảng thay vì chỉ các phần tử riêng lẻ (tức là không có vòng lặp).

Tại sao lại vectorize?. Nó bao gồm các lý do sau:

  1. Nhanh hơn nhiều
  2. Dễ đọc hơn và ít dòng mã hơn
  3. Rất gần với ký hiệu toán học.

Vectorization chính là một trong những lý do vì sao NumPy rất mạnh mẽ.

ndarray

ndarrays, mảng n chiều của kiểu dữ liệu đồng nhất, là kiểu dữ liệu cơ bản được sử dụng trong NumPy. Vì các mảng này cùng kiểu và có kích thước cố định khi tạo, chúng cung cấp độ linh hoạt kém hơn so với danh sách Python, nhưng về cơ bản có thể hiệu quả hơn về thời gian chạy và bộ nhớ. (Danh sách Python là mảng các con trỏ tới các đối tượng, thêm một lớp tham chiếu).

Số chiều chính là rank của mảng đó, shape của array là một tuple số nguyên đưa ra size của mảng theo mỗi chiều.

Có thể tạo ndarray từ Python lists và truy cập vào các phần tử bằng dấu ngoặc vuông như sau:

a = np.array([1, 2, 3])   # Create a rank 1 array
print('type:', type(a))            # Prints "<class 'numpy.ndarray'>"
print('type a[0]', type(a[0]))      # Prints "<class 'numpy.int64'>"
print('shape:', a.shape)            # Prints "(3,)"
print('a:', a)   # Prints "[1 2 3]"
print(a[0])     # Prints "1"

b = np.array([[1, 2, 3],
              [4, 5, 6]])    # Create a rank 2 array
print('shape:', b.shape)                     # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0])   # Prints "1 2 4"

Khi muốn tạo 1 mảng mới = 1 mảng cũ ta khác ta nên sử dụng như sau để khi thay đổi phân tử của mảng thì không ảnh hưởng đến mảng kia.

a_cpy= a.copy()
a[0] = 5                  # Change an element of the array
print('a modeified:', a)                  # Prints "[5, 2, 3]"
print('a copy:', a_cpy)  # Prints "[1 2 3]"

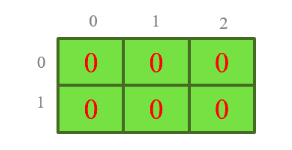
Tạo ndarray với hàm zeros():

a = np.zeros((2, 3))   # Create an array of all zeros shape 2 row 3 col
print(a)               # Prints "[[ 0.  0.]
                       #          [ 0.  0.]]"

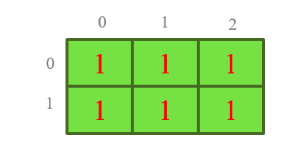
Tạo ndarray với hàm ones():

a = np.ones((2,3))         # Create a 2 x 3 one matrix
print(a)              # Prints "[[ 1. 1. 1.]
                      #          [ 1. 1. 1.]]"

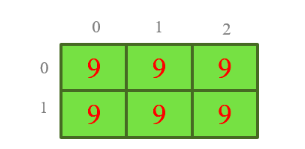
Tạo ndarray với hàm full()

b = np.full((2, 3), 9)  # Create a constant array
print(b)                # Prints "[[ 9.  9.]
                        #          [ 9.  9.]]"

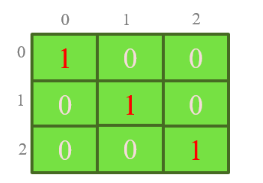
Tạo ma trận đơn vị

c = np.eye(3)         # Create a 3 x 3 identity matrix
print(c)              # Prints "[[ 1.  0.  0.]
                      #          [ 0.  1.  0.]
                      #          [ 0.  0.  1.]]"

Tạo một numpy array với giá trị ngẫu nhiên

d = np.random.random((2, 2))  # Create an array filled with random values
print(d)                      # Might print "[[ 0.91940167  0.08143941]
                              #               [ 0.68744134  0.87236687]]"

Bạn có thể tham khảo nhiều cách tạo ndarry trong documentation.

Dưới đây là 1 số hàm hữu ích để theo dõi shape; hữu ích cho việc gỡ lỗi và biết kích thước sẽ rất hữu ích khi tính toán gradient.

reshape: Cung cấp một hình dạng mới cho một mảng mà không thay đổi dữ liệu của nó.

nums = np.arange(8) 
print(nums)       # Prints "[0 1 2 3 4 5 6 7]"
print(nums.shape) # Prints "(8,)"

nums = nums.reshape((2, 4))
print('Reshaped:\n', nums) 
# output:
# Reshaped:
# [[0 1 2 3]
# [4 5 6 7]]
print(nums.shape)
# output: (2.4)

Trong phương thức reshape(), ta có thể dùng tham số -1 trong việc reshape với một dimension ta không biết mà numpy sẽ tự tìm ra dựa trên tất các các dimensions khác và array size. Bạn có thể xem ví dụ sau để trực quan hơn.

nums = nums.reshape((4, -1))
print('Reshaped with -1:\n', nums, '\nshape:\n', nums.shape)
# output:
#Reshaped with -1:
#[[0 1]
#[2 3]
#[4 5]
#[6 7]] 
#shape:
# (4, 2)

Các cách chuyển mảng về mảng 1 chiều.

nums.reshape(-1)
nums.flatten()
nums.ravel()
# output: [0 1 2 3 4 5 6 7]

Bạn có thể tìm hiểu sự khác nhau của 3 cách trên ở đây

NumPy hỗ trợ một mô hình hướng đối tượng, sao cho ndarray có một số phương thức và thuộc tính, với các hàm tương tự như trong namespace NumPy ngoài cùng. Ví dụ, chúng ta có thể làm cả hai cách và cho kết quả như nhau:

nums = np.arange(8)
print(nums.min())     # Prints 0
print(np.min(nums))   # Prints 0

print(np.reshape(nums, (4, 2)))
print(nums.reshape((4,2)))

print(np.mean(nums))
print(nums.mean())

Datatypes

Mỗi mảng numpy là một lưới các phần tử cùng loại. Numpy cung cấp một tập hợp lớn các kiểu dữ liệu số mà bạn có thể sử dụng để xây dựng các mảng. Numpy cố gắng đoán một kiểu dữ liệu khi bạn tạo một mảng, nhưng các hàm xây dựng các mảng thường cũng bao gồm một đối số tùy chọn để chỉ định rõ ràng kiểu dữ liệu. Đây là một ví dụ:

import numpy as np

x = np.array([1, 2])   # Let numpy choose the datatype
print(x.dtype)         # Prints "int64"

x = np.array([1.0, 2.0])   # Let numpy choose the datatype
print(x.dtype)             # Prints "float64"

x = np.array([1, 2], dtype=np.int64)   # Force a particular datatype
print(x.dtype)                         # Prints "int64"

Bạn có thể đọc tất cả về kiểu dữ liệu numpy trong documentation

Array Operations/Math

Basic math

NumPy hỗ trợ rất nhiều các phép toán cơ bản như sau:

x = np.array([[1, 2],
              [3, 4]], dtype=np.float64)
y = np.array([[5, 6],
              [7, 8]], dtype=np.float64)

# Elementwise sum; cả hai cách đều ra kq như nhau
# [[ 6.0  8.0]
#  [10.0 12.0]]
print(x + y)
print(np.add(x, y))

# Elementwise difference; both produce the array
# [[-4.0 -4.0]
#  [-4.0 -4.0]]
print(x - y)
print(np.subtract(x, y))

# Elementwise product; both produce the array
# [[ 5.0 12.0]
#  [21.0 32.0]]
print(x * y)
print(np.multiply(x, y))

# Elementwise division; both produce the array
# [[ 0.2         0.33333333]
#  [ 0.42857143  0.5       ]]
print(x / y)
print(np.divide(x, y))

# Elementwise square root; produces the array
# [[ 1.          1.41421356]
#  [ 1.73205081  2.        ]]
print(np.sqrt(x))

Dot product

Chú ý * là phép nhân toán tử, không phải là phép nhân ma trận. Thay vào đó chúng ta sử dụng hàm dot để tính tích trong của 2 vector, nhân vector với ma trận, nhân ma trận với ma trận. dot có sẵn ở cả như một hàm củ numpy module hoặc là một instance method của tối tượng array. Ta có thể xem các ví dụ như sau:

x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])

v = np.array([9, 10])
w = np.array([11, 12])

# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))

# Matrix / vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(v, w))

# Matrix / matrix product; both produce the rank 2 array
# [[19 22]
#  [43 50]]
print(x.dot(y))
print(np.dot(x, y))

Across specific axes of the ndarray:

Có nhiều hàm hữu ích được tích hợp trong NumPy và thường chúng ta có thể thể hiện chúng qua các trục cụ thể của ndarray: Các trục với mảng 2 chiểu được thể hiện như trên.

x = np.array([[8, 9], 
              [10, 11],
              [12, 13]])

print(np.sum(x))          # Compute sum of all elements; prints "63"
print(np.sum(x, axis=0))  # Compute sum of each column; prints "[30 33]"
print(np.sum(x, axis=1))  # Compute sum of each row; prints "[17 21 25]"

print(np.max(x, axis=1))  # Compute max of each row; prints "[9 11 13]"

Làm thế nào để chúng ta có thể chỉ ra chỉ số (index) của giá lớn nhát ở mỗi hàng ? Bạn có thể viết như sau:

x = np.array([[1, 2, 3], 
              [4, 5, 6]])

print(np.argmax(x, axis=1)) # Compute index of max of each row; prints "[2 2]"

Chúng ta có thể tìm thấy các chỉ số (index) của các phần tử thỏa mãn một số điều kiện nào đó bằng cách sử dụng np.where:

x = np.array([[1, 2, 3], 
              [4, 5, 6]])

print(np.where(nums > 5)) # Prints (array([6, 7]),)
print(nums[np.where(nums > 5)]) # Prints [6 7]

Lưu ý khi bạn áp dụng các thao tác sẽ loại bỏ chiểu củ nó ra khởi hình dạng (shape). Điều này rất hữu ích để ghi nhớ khi bạn đang cố gắng tìm trục nào tương ứng với cái gì. Ví dụ sau sử dụng hàm ndim chỉ số chiều của mảng.

x = np.array([[1, 2, 3], 
              [4, 5, 6]])

print('x ndim:', x.ndim) # sẽ in ra 2 vì x có 2 chiều
print((x.max(axis=0)).ndim) # trả ra mảng gồm các phần tử max theo cột có shape(3,0) 
                             # khi thêm ".ndim" sẽ trả ra là 1 vì mảng có 1 chiều.

# An array with rank 3
x = np.array([[[1, 2, 3], 
               [4, 5, 6]],
              [[10, 23, 33], 
               [43, 52, 16]]
             ])

print('x ndim:', x.ndim)               # Has shape (2, 2, 3)
print((x.max(axis=1)).ndim) # Taking the max over axis 1 has shape (2, 3)
print((x.max(axis=(1, 2))).ndim)       # Can take max over multiple axes; prints [6 52]

Transposing

Ngoài việc tính toán các hàm toán học bằng cách sử dụng các mảng, chúng ta thường cần phải định hình lại hoặc thao tác dữ liệu trong các mảng. Ví dụ đơn giản nhất của loại hoạt động này là chuyển vị (transposing) ma trận; để hoán vị một ma trận, chỉ cần sử dụng thuộc tính T của một array object:

import numpy as np

x = np.array([[1,2], [3,4]])
print(x)    # Prints "[[1 2]
            #          [3 4]]"
print(x.T)  # Prints "[[1 3]
            #          [2 4]]"

# Chú ý rằng chuyển vị 1 mảng có rank = 1 không thay đổi gì cả:
v = np.array([1,2,3])
print(v)    # Prints "[1 2 3]"
print(v.T)  # Prints "[1 2 3]"

Bạn có thể tìm thấy danh sách đầy đủ các hàm toán học được cung cấp bởi numpy tại đây

Vertical & Horizontal Stacking:

Tiếp theo, nếu bạn muốn nối hai mảng và không chỉ thêm chúng, bạn có thể thực hiện nó bằng hai cách - xếp chồng dọc và xếp chồng ngang.

import numpy as np
x= np.array([(1,2,3),(3,4,5)])
y= np.array([(1,2,3),(3,4,5)])
print(np.vstack((x,y)))
print(np.hstack((x,y)))

Và kết quả nó sẽ ra như sau:

[[1 2 3]
 [3 4 5]
 [1 2 3]
 [3 4 5]]
[[1 2 3 1 2 3]
 [3 4 5 3 4 5]]

Array indexing

Numpy cung cấp một số cách để truy xuất phần tử trong mảng

Slicing: Tương tự như list trong python, numpy arrays cũng có thể được cắt (sliced). Vì các mảng có thể là đa chiều, bạn phải chỉ định một lát cho mỗi chiều của mảng. Ví dụ.

# Tạo một numpy array có shape (3, 4) với giá trị như sau:
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = np.array([[1, 2, 3, 4],
              [5, 6, 7, 8],
              [9, 10, 11, 12]])
print('Original:\n', a)

# Can select an element as you would in a 2 dimensional Python list
print('Element (0, 0) (a[0][0]):\n', a[0][0])   # Prints 1
# or as follows
print('Element (0, 0) (a[0, 0]) :\n', a[0, 0])  # Prints 1

# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
#  [6 7]]
print('Sliced (a[:2, 1:3]):\n', a[:2, 1:3])

# Steps are also supported in indexing. The following reverses the first row:
print('Reversing the first row (a[0, ::-1]) :\n', a[0, ::-1]) # Prints [4 3 2 1]

# slice by the first dimension, works for n-dimensional array where n >= 1
print('slice the first row by the [...] operator: \n', a[0, ...])

Thông thường, thật hữu ích khi chọn hoặc sửa đổi một phần tử từ mỗi hàng của ma trận. Ví dụ sau sử dụng fancy indexing, trong đó chúng ta lập chỉ mục vào mảng của chúng tôi bằng cách sử dụng một mảng các chỉ số (giả sử một mảng các số nguyên hoặc booleans):

# Tạo một mảng mới
a = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9],
              [10, 11, 12]])

print(a)  # prints "array([[ 1,  2,  3],
          #                [ 4,  5,  6],
          #                [ 7,  8,  9],
          #                [10, 11, 12]])"

# Tạo một mảng chỉ số
b = np.array([0, 2, 0, 1])

# Chọn một phần tử từ mỗi hàng của a bằng cách sử dụng các chỉ số trong b
print(a[np.arange(4), b])  # Prints "[ 1  6  7 11]"

# same as
for x, y in zip(np.arange(4), b):
    print(a[x, y])

c = a[0]
c[0] = 100
print(a)

# Đột biến một phần tử từ mỗi hàng của a bằng cách sử dụng các chỉ số trong b
a[np.arange(4), b] += 10

print(a)  # prints "array([[11,  2,  3],
          #                [ 4,  5, 16],
          #                [17,  8,  9],
          #                [10, 21, 12]])

Boolean array indexing: Cho phép bạn chọn ra các phần tử tùy ý của một mảng, thường được sử dụng để chọn ra các phần tử thỏa mãn điều kiện nào đó. Ví dụ ta thay đổi giá trị các phần tử trong mảng lớn hơn MAX = 5 thành 1 số khác như 100

MAX = 5
nums = np.array([1, 4, 10, -1, 15, 0, 5])
print(nums > MAX)         # Prints [False, False, True, False, True, False, False]

nums[nums > MAX] = 100
print(nums)               # Prints [  1   4 100  -1 100   0   5]

Hoặc ví dụ in ra các phần tử thỏa mãn điều kiện nào đó :

x = np.arange(8) 
print(x[x>3]) # Prints "[4 5 6 7]"

Nếu bạn muốn tìm hiều nhiều hơn về numpy array indexing bạn có thể tham khảo tại documentation

broadcasting

Nhiều phép toán chúng ta đã xem xét ở trên là các mảng cùng rank. Tuy nhiên, nhiều lần chúng ta có thể có một mảng nhỏ hơn và sử dụng nhiều lần để cập nhật một mảng có kích thước lớn hơn. Ví dụ, hãy xem xét ví dụ dưới đây về việc dịch chuyển giá trị trung bình của mỗi cột từ các thành phần của cột tương ứng:

x = np.array([[1, 2, 3],
              [3, 5, 7]])
print(x.shape)  # Prints (2, 3)

col_means = x.mean(axis=0)
print(col_means)          # Prints [2. 3.5 5.]
print(col_means.shape)    # Prints (3,)
                          # Has a smaller rank than x!

mean_shifted = x - col_means
print('\n', mean_shifted)
print(mean_shifted.shape)  # Prints (2, 3)

Hoặc như nhân một ma trân với 2:

x = np.array([[1, 2, 3],
              [3, 5, 7]])
print(x * 2) # Prints [[ 2  4  6]
             #         [ 6 10 14]]

Broadcasting 2 arrays với nhau tuân theo các quy luật sau:

  1. Nếu các mảng không cùng rank, sẽ thêm vào shape của mảng low rank với 1 cho đến khi shape của cả 2 mảng có cùng length
  2. Hai mảng được coi là tương thích về dimension nếu chúng có cùng size trong dimension hoặc 1 trong các mảng có size 1 trong dimension đó.
  3. Các mảng có thể broadcast nếu chúng tương thích ở tất cả các chiều.
  4. Sau khi broadcasting, mỗi mảng hoạt động như thể nó có shape bằng maximum of shapes của 2 mảng đầu vào.
  5. Trong bất kỳ dimensionnào trong đó một mảng có kích thước 1 và mảng khác có kích thước lớn hơn 1, mảng đầu tiên hoạt động như thể nó được sao chép dọc theo dimensionđó.

Để cho dễ hiểu, thì khi thực hiện phép trừ cột ở trên, chúng ta có các mảng có shape (2,3) và (3,).

  1. Các mảng này không có cùng thứ hạng, vì vậy chúng ta bổ sung 1 vào shape của mảng thấp rank hơn để tạo ra shape (1,3).
  2. (2, 3) và (1, 3) tương thích (có cùng size trong dimension hoặc nếu một trong các mảng có size 1 trong dimension đó).
  3. Có thể được broadcast cùng nhau!
  4. Sau khi broadcasting, mỗi mảng hoạt động như thể nó có shape bằng (2, 3).
  5. Mảng nhỏ hơn sẽ hoạt động như thể nó được sao chép dọc theo chiều 0. (theo cột )

Bây giời, hãy thử trừ đi giá trị của mỗi hàng.

x = np.array([[1, 2, 3],
              [3, 5, 7]])

row_means = x.mean(axis=1)
print(row_means)  # Prints [2. 5.]

mean_shifted = x - row_means

Khi bạn chạy nó sẽ báo lỗi. Để tìm ra lỗi ta thử in ra shape của 2 mảng.

x = np.array([[1, 2, 3],
              [3, 5, 7]])
print(x.shape)  # Prints (2, 3)

row_means = x.mean(axis=1)
print(row_means)        # Prints [2. 5.]
print(row_means.shape)  # Prints (2,)

Khi nhìn vào shape của 2 mảng, ta có thể tìm ra đáp vì sao chương trình của ta như sau: Nếu chúng ta tuân theo quy tắc 1 thì chúng ta sẽ bổ sung 1 cho mảng có rank nhỏ hơn và sẽ được mảng mới có shape là (1,2). Tuy nhiên chiều cuối cùng không khớp giữ (2,3) và (1,2), vi vậy 2 mảng trên không thể broadcast.

Để cho chương trình như mong muốn, ra phải reshape lại row_means như sau:

x = np.array([[1, 2, 3],
              [3, 5, 7]])
print(x.shape)  # Prints (2, 3)

row_means = x.mean(axis=1)
print('row_means shape:', row_means.shape)
row_means = row_means.reshape(2,1)

mean_shifted = x - row_means
print(mean_shifted)
print(mean_shifted.shape)  # Prints (2, 3)

Các hàm hỗ trợ broadcasting được gọi là universal functions. Bạn có thể tìm danh sách các hàm universal functions tại documentation

Views vs. Copies (option)

Không giống như copy, trong một view của một mảng, dữ liệu được chia sẻ giữa chế độ view và array. Đôi khi kết quả của chúng ta là bản sao của một mảng, nhưng lần khác chúng có thể là views. Hiểu khi nào chúng được tạo ra là một việc quan trọng để tránh các vấn đề bạn không thể lường trước được.

Views có thể tạo từ slice của một mảng, thay đổi dtype của cùng một vùng dữ liệu (sử dụng arr.view(dtype), không phải kết quả của arr.astype(dtype)).

Ta sẽ xem qua các ví dụ sau để có thể hiểu rõ về view hơn.

import numpy as np
x = np.arange(5)
print('Original:\n', x)  # Prints [0 1 2 3 4]

# Modifying the view will modify the array
view = x[1:3]
view[1] = -1
print('Array After Modified View:\n', x)  # Prints [0 1 -1 3 4]

x = np.arange(5)
view = x[1:3]
view[1] = -1

# Modifying the array will modify the view
print('View Before Array Modification:\n', view)  # Prints [1 -1]
x[2] = 10
print('Array After Modifications:\n', x)          # Prints [0 1 10 3 4]
print('View After Array Modification:\n', view)   # Prints [1 10]

Tuy nhiên khi chúng ta sử dụng fancy indexing (được giới hiệu ở phần indexing bên trên) thì kết quả chắc chắn là một copy, không phải một view.

Ví dụ 1:

x = np.arange(5)
print('Original:\n', x)  # Prints [0 1 2 3 4]

# Modifying the result of the selection due to fancy indexing
# will not modify the original array.
copy = x[[1, 2]]
copy[1] = -1
print('Copy:\n', copy) # Prints [1 -1]
print('Array After Modified Copy:\n', x)  # Prints [0 1 2 3 4]

Ví dụ 2:

# Another example involving fancy indexing
x = np.arange(5)
print('Original:\n', x)  # Prints [0 1 2 3 4]

copy = x[x >= 2]
print('Copy:\n', copy) # Prints [2 3 4]
x[3] = 10
print('Modified Array:\n', x)  # Prints [0 1 2 10 4]
print('Copy After Modified Array:\n', copy)  # Prints [2 3 4]

Summary

Những kiến thức trên mình thấy đó là những thứ cốt lõi nhất để bạn có thể hiểu và vận dụng chúng trong các trương trình. Nếu thấy hay thì bạn ngại gì mà không để lại 1 upvote để cho mình thêm động lực viết các bài tiếp theo 😆. Nếu có bất kỳ thắc mắc nào bạn có thể comment bên dưới.

References

Numpy Python

All rights reserved

Mục lục


Viblo
Hãy đăng ký một tài khoản Viblo để nhận được nhiều bài viết thú vị hơn.
Đăng kí