Introduction

Trong bài viết này, ta sẽ cùng tìm hiểu về giải chuỗi trình tự gen - đây cũng là bài báo cáo của mình trong môn tin sinh học mình học ở kì trước mà mình lười giờ mới có dịp đăng để mọi người có thể hiểu thêm 1 chút về một môn rất thú vị kết hợp giữa sinh học và tin học này.

Newspaper Problem

Trước khi đi vào chi tiết về giải trình tự bộ gen thì chúng ta sẽ đi vào một ví dụ cho dễ hiểu hơn. Tưởng tượng ta đặt một xấp một trăm tờ báo bản sao ấn bản ngày 27 tháng 6 năm 2000 của tờ báo New York Time trên đống thuốc nổ và cho nổ. Ta tiếp tục tưởng tượng rằng các tờ báo không bị thiêu hiểu hết mà thay vào đó thành các tàn mảnh giấy nhỏ cháy âm ỉ. Làm sao chúng ta có thể sử dụng những mẩu báo nhỏ này để tìm ra tin tức ngày 27/6/2000 ? Chúng ta gọi vấn đề hóc búa này là Newspaper Problem.

Vấn đề trên còn khó hơn tưởng tượng bởi vì ta có nhiều bản sao của cùng một ấn bản tờ báo, và chắc chắn ta cũng mất thông tin trong vụ nổ, chúng ta không thể lắp ráp như một trò chơi ghép hình bình thường. Thay vào đó, ta cần sử dụng sự chồng chéo từ các bản sao khác nhau của tờ báo để tái tạo tin tức trong ngày.

Genome sequencing

Bạn sẽ tự hỏi, vấn đề trên liên quan gì đến sinh học ? Xác định trình tự các nucleotide (As, Ts, Cs và Gs) trong một gen (hay còn gọi là ADN), hay trình tự bộ gen (Genome sequencing) là một trong những nhiệm vụ cơ bản của tin sinh học. Bộ gen của chính chúng ta có độ dài khoảng 3 tỷ nucleotide.

Bộ gen được giải trình tự đầu tiên, thuộc về một vi khuẩn φX174 chỉ có 5.386 nucleotide và được hoàn thiện vào năm 1977 bởi Frederick Sanger . Bốn thập kỷ sau phát hiện đoạt giải Nobel này, giải trình tự gen đã dẫn đầu trong nghiên cứu tin sinh học, khi chi phí giải trình tự giảm mạnh. Do chi phí giải trình tự ngày càng giảm, chúng ta hiện có hàng nghìn bộ gen được giải trình tự, bao gồm cả bộ gen của nhiều loài động vật có vú.

Hình những động vật có vú đầu tiên có bộ gen được giải trình tự.

The purpose of genome sequencing

• Trong nghiên cứu cơ bản, giải trình tự có thể hỗ trợ xây dựng bản đồ nhiễm sắc thể, thu được thông tin về cấu trúc, chức năng, hoạt động của các đoạn ADN; định danh loài …

• Trong khoa học y tế, giải trình tự DNA có thể được sử dụng để xác định các gen chịu trách nhiệm cho các rối loạn di truyền. Khi có đủ hiểu biết về cấu trúc, chức năng của các đoạn ADN, chúng ta có thể dự đoán nguy cơ phát sinh các hội chứng, bệnh di truyền ở một người hay định hướng phương pháp điều trị bằng việc giải trình tự hệ gen người đó.

• Trong khoa học pháp y, ADN được xem như dấu vân tay phân tử; nó được sử dụng để xác minh huyết thống, điều tra tội phạm và nhận dạng cá nhân. Cái này chắc cái bạn biết đến nhiều hơn qua các phim .

• Trong các ngành nông nghiệp, việc xác định các loài GMO có thể được thực hiện với sự trợ giúp của các phương pháp giải trình tự ADN. Bất kỳ biến thể nhỏ nào trong bộ gen thực vật đều có thể được phát hiện với sự trợ giúp của trình tự DNA.

Difficulties and challenges

Để giải trình tự một bộ gen, chúng ta phải giải quyết một số rào cản thực tế.

1. Trở ngại lớn nhất là thực tế là các nhà sinh học vẫn thiếu công nghệ để đọc các nucleotide của bộ gen từ đầu đến cuối giống như cách bạn đọc một cuốn sách. Điều tốt nhất họ có thể làm là trình tự các đoạn DNA ngắn hơn nhiều được gọi là reads. DNA là dạng chuỗi kép, và chúng ta không có cách nào biết được tiên nghiệm mà chuỗi mà của một số reads nhất định bắt nguồn từ đâu, có nghĩa là chúng ta sẽ không biết nên sử dụng read này hay phần bổ sung ngược lại của nó khi lắp ráp một chuỗi cụ thể của bộ gen.
2. Khó khăn thứ 2 là các máy giải trình tự gen hiện tại không hoàn hảo và các reads mà chúng tạo ra thường có lỗi. Các lỗi sắp xếp trình tự làm phức tạp quá trình lắp ráp bộ gen vì chúng ngăn ta xác định tất cả các reads chồng chéo.
3. Thứ 3 là một số vùng của bộ gen có thể không được bao phủ bởi bất kỳ reads nào, khiến cho việc tái tạo lại của toàn bộ bộ gen là điều không thể.

Phương pháp truyền thống để giải trình tự gen sẽ như sau: Các nhà nghiên cứu lấy một mô nhỏ hoặc mẫu máu chứa hàng triệu tế bào có DNA giống hệt như nhau, sử dụng phương pháp sinh hóa để bẻ gãy DNA thành các fragments (các đoạn) và trình tự của các fragments đó trở thành reads.

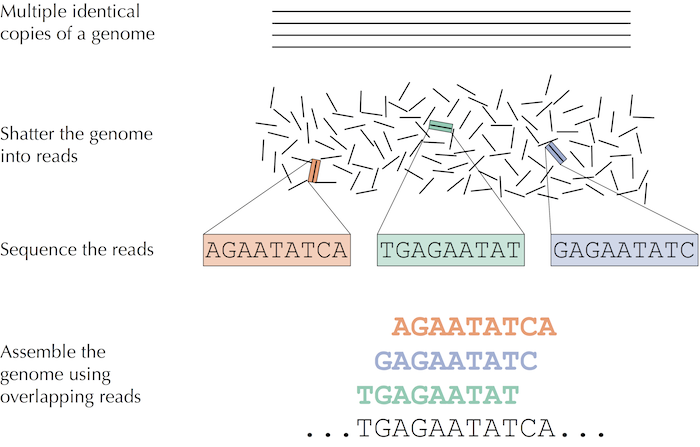
Hình: trong giải trình tự DNA, nhiều bản sao giống hệt nhau của bộ gen bị phá vỡ ở vị trí ngẫu nhiên để tạo ra các short reads, sau đó giải trình tự và lắp ráp thành trình tự nucleotide của bộ gen.

Ta có thể xem các bước rõ hơn trong thực tế ở ảnh sau:

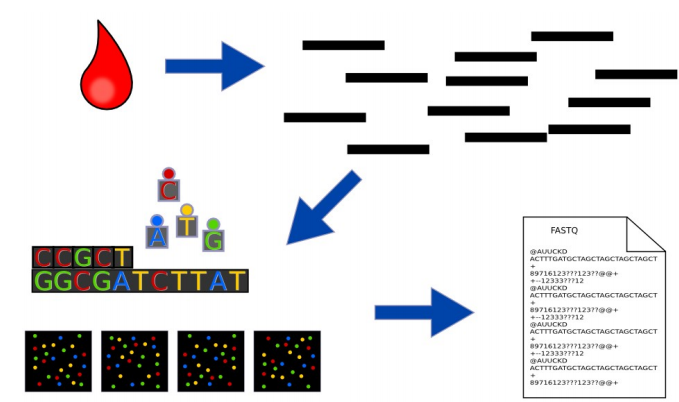
Hình: sau các bước thì kết quả sẽ lưu ở định dạng FASTQ. Bạn đọc có thể vào https://en.wikipedia.org/wiki/FASTQ_format để biết thêm chi tiết.

Các nhà nghiên cứu không biết các reads này từ đâu trong bộ gen, vì vậy họ phải sử dụng những reads chồng chéo để tái tạo bộ gen. Vì vậy, việc đặt một bộ gen trở lại từ việc các reads của nó hay genome assembly (tập hợp bộ gen) giống y Newspaper Problem

Sequence assembly

Trong bài viết này, chúng ta sẽ tìm hiểu về shotgun sequencing là một phương pháp được sử dụng để giải trình tự các sợi DNA ngẫu nhiên ( ta có thể tưởng tượng là như súng shotgun khi bắn đạn sẽ vỡ thành từng mảng ngẫu nhiên). Có 2 cách tiếp cận để lắp ráp các trình tự shotgun reads thành các chuỗi gen liền kề dài hơn là:

• Cách tiếp cận lắp ráp trình tự de novo, các reads được so sánh với nhau, sau đó được chồng lên nhau để xây dựng liền kề dài hơn ( không sử dụng thêm kiến thức nào).
• Cách tiếp cận dựa trên tham chiếu liên quan đến việc ánh xạ mỗi read tới một trình tự bộ gen tham chiếu ( sử dụng kiến thức dựa trên tham chiếu)

De novo sequence assembly

Vì reads được tạo bởi các trình tự hiện tại thường có cùng độ dài, chúng ta có thể giả định một cách an toàn rằng reads đều là k-mers với 1 số giá trị k. Phần đầu của bài sẽ giả định một tình huống lý tưởng và không thực tế là tất cả các read đều đến từ cùng một chuỗi, không có lỗi và thể hiện mức độ bao phủ hoàn hảo. Sau đó, ta sẽ trình bày cách giảm bớt các giả định này để có bộ dữ liệu thực tế hơn.

The String Reconstruction Problem

Cho một chuỗi Text, k-mer composition ký hiệu là $Composition_{k}(Text)$ là tập hợp các chuỗi con k-mer của Text ( bao gồm cả các k-mers lặp).

Ví dụ $Composition_{3}(TATGGGGTGC) = {ATG, GGG, GGG, GGT, GTG, TAT, TGC, TGG}$. Chú ý rằng ở đây ta liệt kê k_mer theo thứ tự từ điển chứ không phải thứ tự của nó xuất hiện trong chuỗi TATGGGGTGC. Ta làm điều này vì thứ tự chính xác của các reads không được biết khi nào chúng được tạo ra.

Giải bài toán tìm tập hợp các k-mer từ một chuỗi là đơn giản, nhưng để tập hợp thành một bộ gen, chúng ta cần bài toán nghịch đảo của nó: xây dựng chuỗi từ k-mers.

Trước khi chúng ta giải quyết vấn đề tái tạo chuỗi, hãy xem ví dụ sau về các thành phần 3-mer: AAT , ATG , GTT, TAA, TGT.

Cách tự nhiên nhất để giải Bài toán tái lập chuỗi là bắt chước cách giải của Bài toán báo và "nối" một cặp k -mers nếu chúng trùng nhau k -1 ký tự. Đối với ví dụ trên, dễ dàng thấy rằng chuỗi phải bắt đầu bằngTAA bởi vì không có 3-mer kết thúc bằng TA. Điều này ngụ ý rằng 3-mer tiếp theo trong chuỗi phải bắt đầu bằng AA. Chỉ có một 3-mer thỏa mãn điều kiện này là AAT, ta được: TAA AAT. Tiếp theo, AAT tiếp sau nó chỉ có thể là ATG, sau ATG sẽ là TGT, tiếp tục như thế ta được chuỗi TAATGTT.

Có vẻ ta đã giải quyết bài toán tái tạo chuỗi ? nhưng để chắc chắn ta thêm một số thành phần 3-mer nữa như sau:

Nếu chúng ta bắt đầu lại TAA, 3-mer tiếp theo trong chuỗi sẽ bắt đầu với AA và chỉ có AAT, tiếp sau ATT chỉ có ATG.

ATG tiếp theo sau sẽ là TGC, TGG, TGT. Chúng ta sẽ thử chọn TGT:

Sau TGT, chúng ta chỉ có thể chọn GTT:

Đến đây thì bế tắc vì không có 3-mer bắt đầu TT!. Chúng ta có thể mở rộng TAA sang bên trái nhưng không có 3-mer nào kết thúc bằng TA.

Chuỗi đúng phải là TAATGCCATGGGATGTT.

Khó khăn trong việc lắp ráp bộ gen mô phỏng này nảy sinh bởi vì ATG được lặp lại 3 lần, khiến chúng ta có ba lựa chọn TGG, TGC và TGT bằng cách đó để mở rộng ATG. Các chuỗi con lặp đi lặp lại trong hệ gen không phải là vấn đề nghiêm trọng khi chúng ta chỉ có 15 reads, nhưng với hàng triệu reads, việc lặp lại khiến việc "nhìn trước" và xây dựng tập hợp chính xác trở nên khó khăn hơn nhiều. Thật vậy, khoảng 50% bộ gen người được tạo thành từ các lần lặp lại, ví dụ, trình tự Alu dài khoảng 300 nucleotit được lặp lại hơn một triệu lần, với chỉ một vài nucleotit được chèn / xóa / thay thế mỗi lần.

String Reconstruction as a Walk in the Overlap Graph

Sự lặp lại trong một bộ gen đòi hỏi một số cách nhìn trước để xem trước sự lắp ráp chính xác. Quay trở lại ví dụ trên ta thấy rằng $TAATGCCATGGGATGTT$ là một lời giải của 15 thành phần 3-mers như hình minh họa sau:

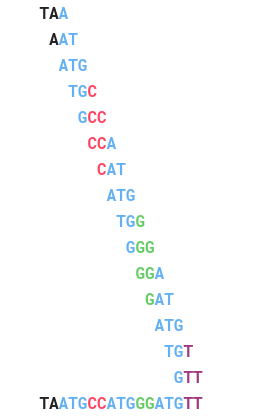
Trong hình dưới, 3-mers liên tiếp trong $TAATGCCATGGGATGTT$ được liên kết với nhau với nhau thành genome path của chuỗi này. Ở đây, ta sẽ áp dụng quy tắc là hậu tố tương ứng với k-1 ký tự cuối của thành phần này nếu là tiền tố của k-1 ký tự đầu thành phần kia thì sẽ có mối liên kết giữa chúng. Ví dụ, Prefix(TAA) = TA và Suffix(TAA) = AA.

Quan sát này cho thấy một phương pháp xây dựng đường bộ gen của một chuỗi từ nó k -mer thành phần: chúng ta sẽ sử dụng một mũi tên để kết nối bất kỳ k -mer mẫu này để một k -mer mẫu kia nếu hậu tố của mẫu này bằng tiền tố của mẫu kia.

Nếu ta tuân thủ nghiêm ngặt quy tắc trên, thì ta sẽ nối tất cả các 3-mer trong $TAATGCCATGGGATGTT$, tuy nhiên chúng ta không biết trước về bộ gen này chỉ biết các 3-mer nên chúng ta cũng phải kết nối nhiều cặp 3-mer khác.

Hình trên là đồ thị có hướng theo mũi tên gồm 15 nút và 28 cạnh hiển thị tất cả các kết nối giữa các nút đại diện cho thành phần 3-mer, lưu ý bộ gen vẫn có thể viết ra bằng cách đi dọc từ TAA đến GTT.

Nhưng trong giải trình tự bộ gen, chúng ta không biết trước làm thế nào để sắp xếp chính xác reads. Do đó, chúng ta sẽ sắp xếp từ vựng 3 mers, tạo ra đồ thị chồng chéo được hiển thị trong hình bên dưới. Genome path đã biến mất!

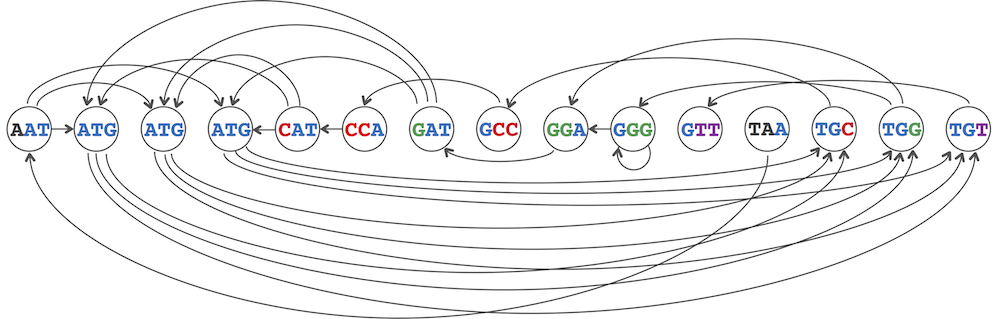
Hình overlap_graph.png: Genome path đã biến mất với mất thường những nó vẫn ở đó, vì chúng ta chỉ đơn giản là sắp xếp các nút của đồ thị.

Nếu chúng ta cho bạn đồ thị overlap_graph trên để bắt đầu, bạn sẽ cần phải tìm đường đi trong đồ thị sao cho đi qua mỗi nút chính xác một lần. Một con đường như thế sẽ đưa ra cho ta một bộ gen. Mặc dù việc tìm ra một con đường như vậy hiện khó khăn như việc cố gắng lắp ráp bộ gen bằng tay, tuy nhiên, biểu đồ cho chúng ta một cách hay để hình dung mối quan hệ chồng chéo giữa reads.

Hình overlap_graph_alternate.png: đường dẫn bộ gen $TAATGCCATGGGATGTT$, highlight trong đồ thị chồng chéo.

Nếu bạn chưa làm việc với dữ liệu đồ thị trước đây, thì ở đây tôi giới thiệu 2 cách đơn biểu diễn đồ thị trong lập trình là sử dụng adjacency matrix (ma trận kề) và adjacency list ( danh sách kề).

Bây giờ chúng ta biết rằng để giải quyết vấn đề tái thiết chuỗi, chúng ta đang tìm kiếm một đường dẫn trong biểu đồ chồng chéo mà truy cập chính xác mỗi nút một lần. Một đường trong biểu đồ truy cập mỗi nút một lần được gọi là đường Hamilton , để vinh danh nhà toán học người Ireland William Hamilton. Nhưng bài toán Hamilton thì chưa có thuật toán hiệu quả để giải nó cả.

Thay vào đó chúng ta sẽ gặp Nicolaas de Bruijn, một nhà toán học người Hà Lan. Năm 1946, de Bruijn quan tâm đến việc giải quyết một vấn đề lý thuyết thuần túy, được mô tả như sau. Một chuỗi nhị phân là một chuỗi chỉ gồm 0 và 1 của; một chuỗi nhị phân là k -universal nếu nó chứa mỗi k -mer nhị phân đúng một lần. Ví dụ 0001110100 là một chuỗi 3 phổ quát, vì nó chứa một trong số tám chuỗi 3 nhị phân (000, 001, 011, 111, 110, 101, 010 và 100) chính xác một lần.

Tìm một chuỗi k -universal tương đương với việc giải Bài toán Tái tạo chuỗi khi thành phần k -mer là tập hợp của tất cả các k -mer nhị phân. Do đó, việc tìm một chuỗi k -universal có thể được rút gọn thành việc tìm một đường Hamilton trong đồ thị chồng lấp được hình thành trên tất cả các k -mers nhị phân (xem hình bên dưới). Mặc dù có thể dễ dàng tìm thấy đường đi Hamilton dưới đây bằng tay, de Bruijn quan tâm đến việc xây dựng các chuỗi k -universal cho các giá trị tùy ý của k. Ví dụ, để tìm một 20-universal, bạn sẽ phải xem xét một biểu đồ có hơn một triệu nút. Hoàn toàn không rõ ràng làm thế nào để tìm ra một đường đi Hamilton trong một đồ thị lớn như vậy, hoặc thậm chí liệu một đường đi như vậy có tồn tại hay không!

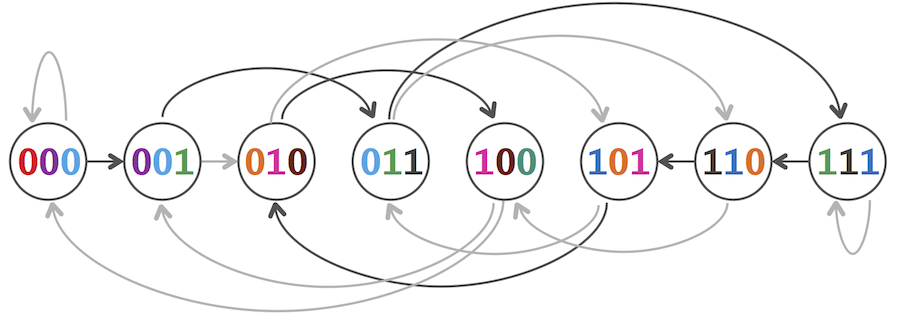
Hình: Một đường đi Hamilton (nút kết nối 000 đến 100) trong đồ thị chồng chéo của tất cả các 3-mers nhị phân.

Thay vì tìm kiếm các đường đi Hamilton trong các đồ thị khổng lồ, de Bruijn đã phát triển một cách hoàn toàn khác để biểu diễn thành phần k -mer bằng cách sử dụng đồ thị. Phần sau của chương này, chúng ta sẽ tìm hiểu cách ông sử dụng phương pháp này để xây dựng các chuỗi phổ quát (universal strings).

Walking in the de Bruijn Graph

Ta quay lại với ví dụ bộ gen TAATGCCATGGGATGTT với chuỗi 3-mers của nó:

Lần này thay vì sử dụng 3-mers làm các nút như trước, ta sẽ dùng nó làm edge (cạnh):

Vì mỗi cặp cạnh liên tiếp đại diện cho 3 nucleotit liên tiếp xen phủ nhau, chúng ta sẽ gắn nhãn mỗi nút của đồ thị này bằng 2-mer đại diện cho các nucleotit chồng chéo được chia sẻ bởi các cạnh ở hai bên của nút.

Sau đó chúng ta gộp các nút giống hệt nhau. Hình dưới ta gộp các AT thành một.

Ta tiếp tục gộp 3 nút TG thành 1 nuts.

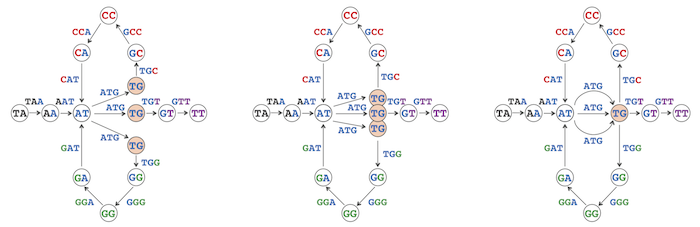
Cuối cùng, chúng ta dán hai nút có nhãn GG, tạo ra một loại cạnh đặc biệt gọi là vòng kết nối GG cho chính nó. Số lượng nút trong biểu đồ kết quả (hiển thị bên phải bên dưới) đã giảm từ 16 xuống còn 11, trong khi số cạnh vẫn giữ nguyên.

Đồ thị này được gọi là đồ thị de Bruijn của $TAATGCCATGGGATGTT$, ký hiệu là $DeBruijn_{3}(TAATGCCATGGGATGTT)$

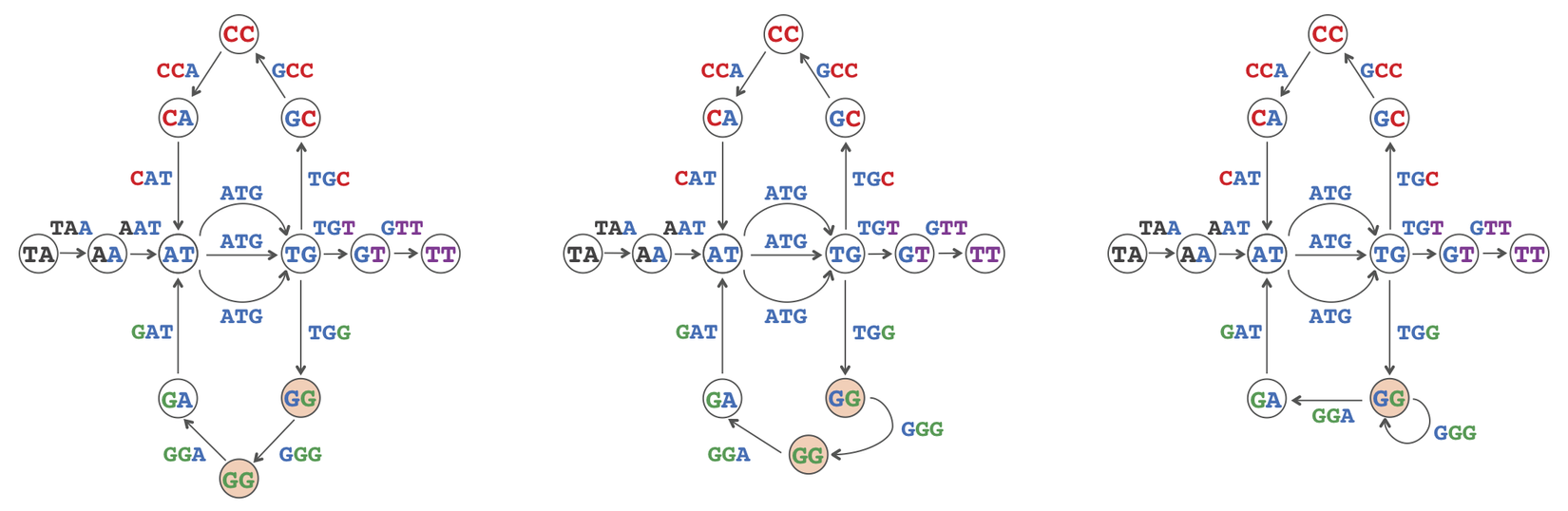
Từ đồ thị de Bruijn của $TAATGCCATGGGATGTT$, việc giải Bài toán tái thiết chuỗi sẽ giảm thành việc tìm đường trong đồ thị de Bruijn mà truy cập chính xác mỗi cạnh một lần. Đường như vậy được gọi là đường đi euler.

Quay ngược vấn đề, ta tạo đồ thị De Bruijn từ các thành phần k-mers: Cho tập hợp Patterns gồm toàn k-mers, các node trong $DeBruijn_{k}(Patterns)$ là tất cả các k-1 mers duy nhất xuất hiện ở tiền tố hoặc hậu tố trong Patterns. Ví dụ cho tập hợp 3-mers:

Sau đó, tập hợp 2-mers duy nhất xuất hiện dưới dạng tiền tố hoặc hậu tố của 3-mers trong tập hợp trên như sau:

Đối với mọi k-mer trong Patterns, chúng ta kết nối nút tiền tố của nó với nút hậu tố của nó bằng một cạnh có hướng để tạo ra DeBruijn(Patterns) như sau:

De Bruijn graphs versus overlap graphs

Bây giờ chúng ta có hai cách để giải Bài toán Tái thiết chuỗi. Chúng ta có thể tìm một đường Hamilton trong overlap graphs (trên) hoặc tìm một đường Euler trong đồ thị de Bruijn (dưới).

Bạn sẽ đặt ra câu hỏi suốt từ đầu bài đến giờ: ta có đáng mất thời gian để học hai cách giải quyết hơi khác nhau cho cùng vấn đề không? Rốt cuộc, ta chỉ thay đổi một từ duy nhất trong phát biểu bài toán đường đi Hamilton và đường đi Eulerian, từ việc một đường đi qua cách nút đúng một lần đến đường đi qua các cạnh đúng một lần.

Dự đoán của tôi là bạn muốn làm việc với đồ thị de Bruijn hơn, vì nó nhỏ hơn. Tuy nhiên, đây sẽ là lý do sai lầm khi chọn một biểu đồ này hơn biểu đồ kia. Trong trường hợp các vấn đề lắp ráp thực sự, cả hai biểu đồ sẽ có hàng triệu nút, và vì vậy tất cả những gì quan trọng là tìm ra một thuật toán hiệu quả để tái tạo lại bộ gen. Nếu chúng ta có thể tìm thấy một thuật toán hiệu quả cho Bài toán đường đi Hamilton, nhưng không cho Bài toán đường đi Eulerian, thì bạn nên chọn overlap graphs mặc dù nó trông phức tạp hơn. Mặt khác, hóa ra là chưa ai có thể tìm ra một thuật toán hiệu quả giải Bài toán Đường đi Hamilton. Việc tìm kiếm một thuật toán như vậy, hoặc một bằng chứng rằng một thuật toán hiệu quả không tồn tại cho vấn đề này, là trọng tâm của một trong những câu hỏi cơ bản nhất chưa được trả lời trong khoa học máy tính, các vấn đề đó được gọ chung với cái tên là NP-complete

Trong hai thập kỷ đầu tiên sau khi phát minh ra phương pháp giải trình tự DNA, các nhà sinh học đã tập hợp các bộ gen bằng cách sử dụng đồ thị chồng chéo, vì họ không nhận ra rằng các cây cầu Königsberg ( chính là bài toán 7 cây cầu nổi tiếng) nắm giữ chìa khóa để lắp ráp DNA. Thật vậy, các overlap graphs đã được sử dụng để lắp ráp bộ gen người. Các nhà thông tin sinh học đã mất một thời gian để tìm ra rằng biểu đồ de Bruijn, lần đầu tiên được xây dựng để giải quyết một vấn đề hoàn toàn lý thuyết, có liên quan đến việc lắp ráp bộ gen. Hơn nữa, khi đồ thị de Bruijn được đưa vào tin sinh học, nó được coi là một khái niệm toán học kỳ lạ với các ứng dụng thực tế hạn chế. Ngày nay, biểu đồ de Bruijn đã trở thành cách tiếp cận chủ đạo để lắp ráp bộ gen.

Vì vậy, ta giải trình tự gen theo hướng tìm đường đi Euler. Chúng ta sẽ đi sâu vào định lý Euler.

Euler's Theorem

Định lý: Đồ thị có hướng là Euler nếu nó liên thông và mọi đỉnh của nó có bậc vào bằng bậc ra.

Trong phần còn lại của phần này, chúng ta sẽ chứng minh Định lý Euler bằng cách giả sử chúng ta có một đồ thị có hướng cân bằng và liên thông mạnh tùy ý và chứng tỏ rằng đồ thị này phải có chu trình Eulerian.

Đặt chú kiến Leo tại bất kỳ nút nào $v_{0}$ của Đồ thị (nút màu xanh lá cây trong hình trên) và để anh ta đi bộ ngẫu nhiên qua biểu đồ với điều kiện anh ta không thể đi qua cùng một cạnh hai lần. Nếu Leo cực kỳ may mắn - hoặc một thiên tài - thì anh ấy sẽ đi qua mỗi cạnh chính xác một lần và quay trở lại$v_{0}$ . Tuy nhiên, tỷ lệ cược là Leo sẽ "mắc kẹt" ở đâu đó trước khi anh ta có thể hoàn thành một chu trình Eulerian, nghĩa là anh ta đến một nút và không tìm thấy cạnh nào chưa sử dụng rời khỏi nút đó.

Hình: Leo tạo ra một chu kỳ $Cycle_{0}$ (được tạo thành bởi các cạnh màu xanh lá cây) khi anh ta bị mắc kẹt tại nút màu xanh lá cây v 0 . Trong trường hợp này, anh ta vẫn chưa đến thăm mọi cạnh trong biểu đồ.

Như chúng ta đã đề cập, nếu $Cycle_{0}$ là Eulerian, chúng ta đã kết thúc. Mặt khác, vì Đồ thị liên thông mạnh, một số nút trên $Cycle_{0}$ phải có các cạnh chưa sử dụng nhập vào nó và rời khỏi nó. Đặt tên cho nút này là $v_{1}$ , chúng ta yêu cầu Leo bắt đầu ở $v_{1}$ thay vì $v_{0}$ và đi qua $Cycle_{0}$ (do đó quay trở lại $Cycle_{1}$ )

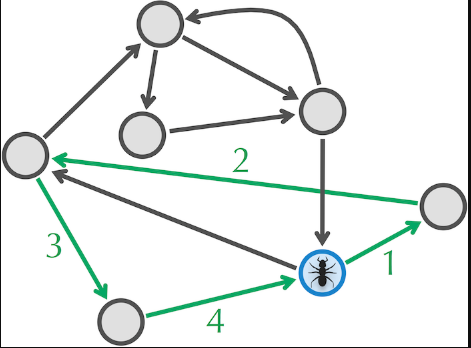
Sau khi đi qua chu kỳ màu xanh lá cây đã xây dựng trước đó $Cycle_{0}$, Leo tiếp tục đi bộ và cuối cùng tạo ra một chu kỳ lớn hơn $Cycle_{1}$ được hình thành từ cả chu kỳ màu xanh lá cây và màu xanh lam gộp lại thành một chu kỳ duy nhất.

Như trước đây, Leo tiếp tục mắc kẹt ở $v_{1}$, nơi anh ấy bắt đầu.Nếu Chu kỳ 1 là chu kỳ Eulerian, thì Leo đã hoàn thành công việc của mình. Nếu không, chúng ta chọn một nút $v_{2}$ trong $Cycle_{1}$ có các cạnh chưa sử dụng nhập vào nó và để lại nó (nút màu đỏ trong hình trên). Bắt đầu từ $v_{2}$ , chúng ta yêu cầu Leo đi qua $Cycle_{1}$ , quay trở lại $v_{2}$ như được hiển thị trong hình bên phải ở trên. Sau đó, anh ta sẽ đi bộ một cách ngẫu nhiên cho đến khi mắc kẹt ở $v_{2}$ , tạo ra một chu kỳ lớn hơn mà chúng ta đặt tên là $Cycle_{2}$ .

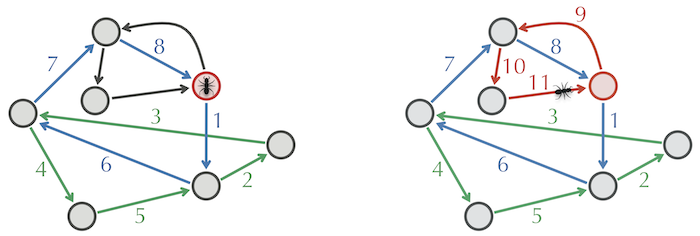
Trong hình trên, Chu kỳ 2 là Eulerian, mặc dù điều này chắc chắn không phải là trường hợp của một đồ thị tùy ý. Nói chung, Leo tạo ra các chu kỳ lớn hơn và lớn hơn ở mỗi lần lặp, và vì vậy chúng ta đảm bảo rằng sớm hay muộn một số Chu kỳ m sẽ đi qua tất cả các cạnh trong Đồ thị . Chu kỳ này phải là Eulerian, và như vậy chúng ta (và Leo) đã kết thúc.

Từ các bước trên ta có mã giả để xay dựng chu trình Euler cho đồ thị Euler như sau:

Bây giờ chúng ta có thể kiểm tra xem một đồ thị có hướng có chu trình Eulerian hay không , nhưng còn đường Eulerian thì sao? Hãy xem xét biểu đồ de Bruijn ở bên trái trong hình bên dưới, mà chúng ta đã biết có đường Eulerian, nhưng không có chu trình Eulerian vì các nút TA và TT không cân bằng. Tuy nhiên, chúng ta có thể biến đổi đường Eulerian này thành một chu trình Eulerian bằng cách thêm một cạnh duy nhất nối TT và TA, như trong hình bên dưới.

Tổng quát hơn, ta xem xét một đồ thị có đường đi Euler nhưng không có chu trình Euler. Nếu 1 đường đi Euler trong đồ thi nối từ nút $v$ đến nút $w$ khác thì đồ thị đó gần như cân bằng vì ngoại trừ 2 nút v và w thì các nút khác đều cân băng ( cạnh vào = cạnh ra ). Do đó, việc thêm cạn phụ nối V và w sẽ biến đồ thì thành đồ thị có chu trình Euler.

Ta có thuật toán từ Eulerian cycles to Eulerian paths:

Reference based mapping/alignment

Như tên gọi ở đây ta sẽ sử dụng một bộ gen được lắp ráp trước đó được sử dụng làm tài liệu tham khảo. Các lần reads theo trình tự được căn chỉnh độc lập với trình tự tham chiếu này. Từng reads được đặt ở vị trí có khả năng nhất

Phương pháp ngây thơ: Đánh giá mọi vị trí trên tham chiếu.

=> Quá chậm với hàng tỷ reads trên một tham chiếu lớn.

Sử dụng chỉ mục để tham chiếu.

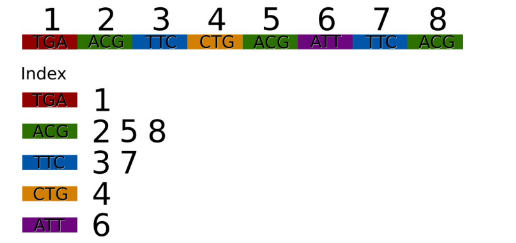
Ở đây, ta sẽ tìm tất cả vị trí căn chỉnh có thể ( gọi là seed) và ta cho Read đánh giá với mọi seed một.

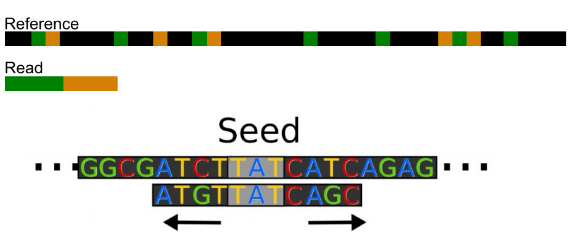
Sau đó, ta xác định sự liên kết tối ưu cho các vị trí ứng viên tốt nhất, tuy nhiên nếu trong read xuất hiện việc chèn hoặc xóa 1 số nucleotide thì sẽ làm tăng độ phức tạp của việc căn chỉnh.

Sử dụng dynamic programming

Đây là phương pháp phổ biến nhất. Những thuật toán hay dùng là Smith-Watherman , Gotoh ...

Bài toán sẽ đưa về xác định các vùng tương tự giữa hai chuỗi của trình tự axit nucleic. Hình dưới mô tả cho thuật toán Smith – Waterman. Mọi người có thể tham khảo ở đường dẫn wikipedia sau : https://en.wikipedia.org/wiki/Smith–Waterman_algorithm

Các khó khăn khi sử dụng phương pháp này.

1. Các reads có thể khác với chuỗi tham chiếu ( các biến thể về cấu trúc).
2. Tham chiếu có nhiều vị trí duplicate Có nhiều chiến lược khác nhau xử lý vấn đề trên:

• Bỏ qua reads
• Đặt ở nhiều vị trí
• Chọn 1 vị trí ngẫu nhiên
• Đặt vào vị trí đầu tiên Các chuỗi không được căn chỉnh có thể được để trong "thùng rác" để xử lý sau vì cần thêm thông tin
• Sequences không phù hợp tại vị trí nào
• Sequences với nhiều vị trí có thể căn chỉnh.

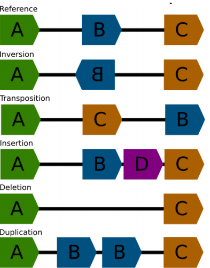
De novo vs. reference

Căn chỉnh dựa trên tham chiếu (Reference based alignment)

• Tốt cho SNV ( single nucleotide variants ), small indels
• Giới hạn về độ dài của Reads để phát hiện ra tính năng.
• Làm việc với deletions và duplications (CNVs - Copy-number variation) + Sử dụng thông tin bao phủ
• Phương pháp này rất nhanh
• Kết quả của việc căn chỉnh không nhất thiết phải tương tự như trình tự tham chiếu
• Yêu cầu phải có trình tự tham chiếu ( reference sequences) tương tự với dữ liệu đầu vào

Lắp ráp De novo

• Cố gắng tạo ra original sequence (trình tự mẫu)
• Tốt cho các biến dị có cấu trúc
• Tốt cho các trình tự hoàn toàn mới không có trong tham chiếu
• Chậm hơn và yêu cầu cơ sở hạ tầng để tính toán

Tóm lại khi bắt đầu giải trình một bộ gen thì ta sẽ sử dụng phương pháp dựa trên tham chiếu.

Reference

1. How do we assemble genomes?
2. GIẢI TRÌNH TỰ GEN TẠI GENLAB
3. https://en.wikipedia.org/wiki/Smith–Waterman_algorithm