Một số khái niệm cần nắm được

• Re-parameterize: Là kĩ thuật thay đổi parameters của một layers (kernel của một lớp Conv) theo dạng biểu diễn khác. Về chi tiết hơn một chút, các bạn có thể đọc ở đây
• Convolution (Conv): Phép tích chập, là phép tính toán chủ đạo trong CNN. Với một input feature maps có chiều $(H, W, C)$, nếu ta thực hiện conv với một filter $(kH, kW, C)$ với same padding thì sẽ tạo ra output feature maps có chiều $(H, W, 1)$. Nếu ta thực hiện conv với C2 filters cũng với same padding thì sẽ tạo ra output feature maps có chiều $(H, W, C2)$. Các bạn cần nắm chắc phép Conv thực sự làm gì. Hình 1 là biểu diễn của phép Conv

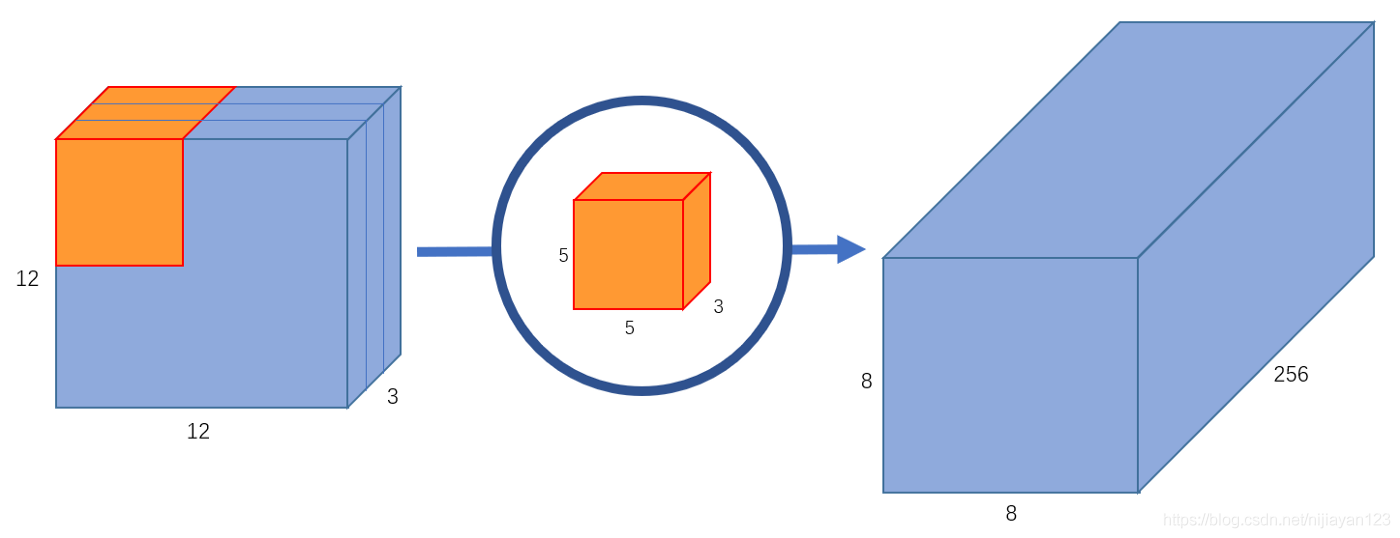
• Depthwise Conv (DWConv): Phép Conv nhưng ta sẽ thực hiện theo chiều channel. Tức là, ở channel thứ $i$ của input feature maps sẽ thực hiện conv với channel thứ $i$ của filter, tạo ra channel thứ $i$ trên output feature maps. Hình 2 biểu diễn phép DWConv

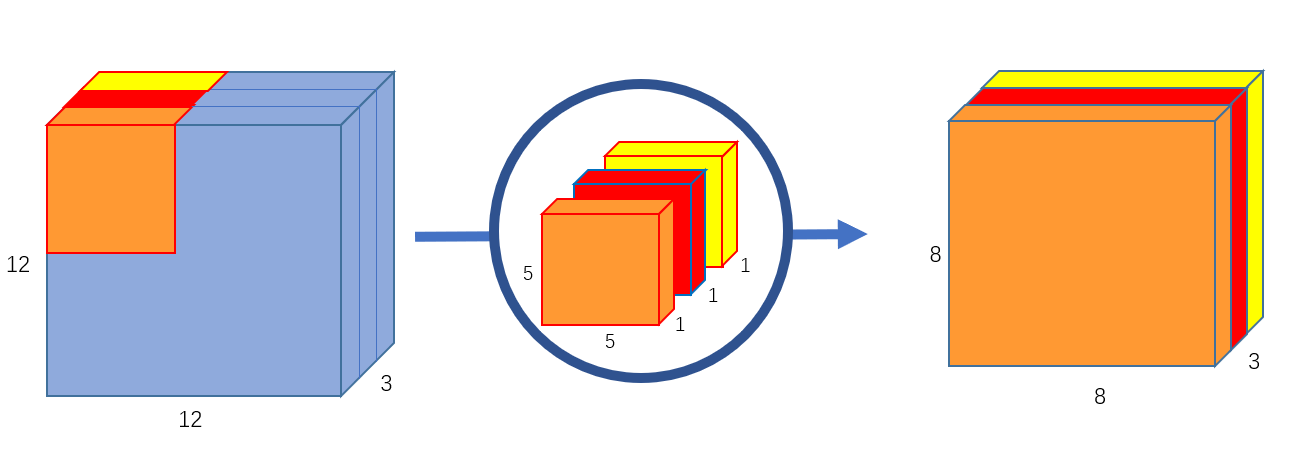
• RepVGG (optional): Khuyến khích các bạn đọc bài này đã có kiến thức về RepVGG, nếu chưa có, các bạn có thể đọc ở đây. Còn mình sẽ nói tóm tắt RepVGG đã làm gì tại bài viết này. Những gì RepVGG làm được thể hiện trong Hình 3: Gộp một khối bao gồm 2 lớp Conv ($3 \times 3$ Conv, $1 \times 1$ Conv) và 3 lớp BatchNorm thành một lớp $3 \times 3$ Conv duy nhất. Nó sẽ training với cái khối gồm nhiều lớp Conv, còn lúc inference (test time) sẽ hóa thân nó thành một lớp Conv thôi.

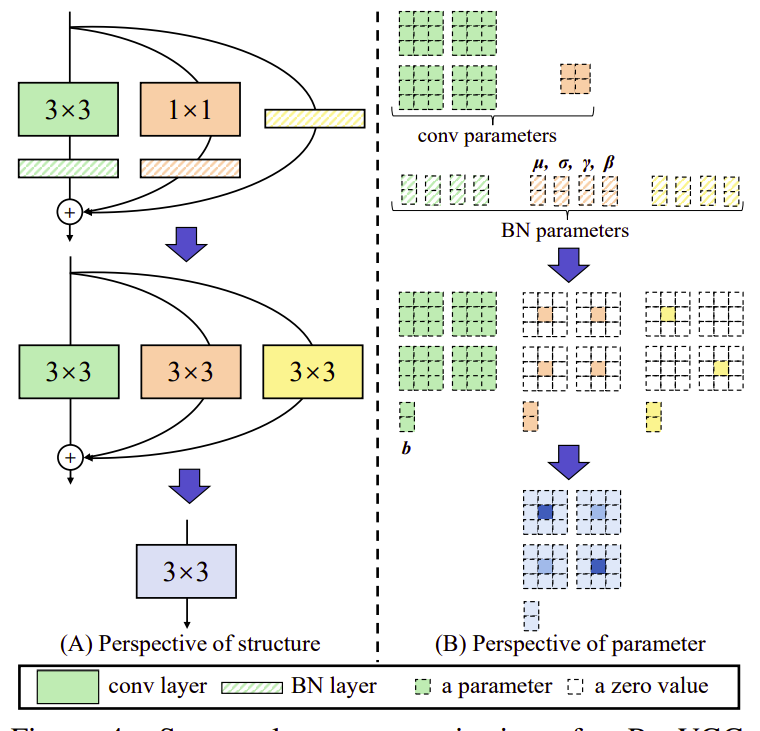
• Trainable operator (trainable ops): Là các layer, hoặc phép toán mà có thể train được, tức là $f_w(x) = y$ thì kết quả của $y$ sẽ phụ thuộc cả vào input $x$ và weight $w$
• Constant operator (constant ops): Là các layer, hoặc phép toán mà không train được, tức là $f(x) = y$ thì kết quả của $y$ sẽ chỉ phụ thuộc vào input $x$

Rep-Optimizer

Vấn đề của RepVGG, hay các Rep-model khác

RepVGG là một ý tưởng tuyệt vời cho thấy sự hiệu quả của kĩ thuật Re-param trong test time. Tuy nhiên, đó chỉ là trong test time. Tức là trong lúc training, bản chất ta vẫn phải train một mô hình khá là to khiến thời gian training lâu. Đối với các team, công ty đã có nguồn tài nguyên dồi dào để training thì đây không phải là vấn đề, tuy nhiên đối với các team eo hẹp trong kinh phí, hay các bạn sinh viên thì nó sẽ khá là khó chịu.

Hơn nữa, việc sử dụng kĩ thuật quantization lên các Rep-model cũng khá là khó khăn. Sau khi thực hiện INT8 quantization lên RepVGG, accuracy của nó đã tụt dốc không phanh, xuống thẳng $54.55\%$ trên ImageNet

Hướng giải quyết

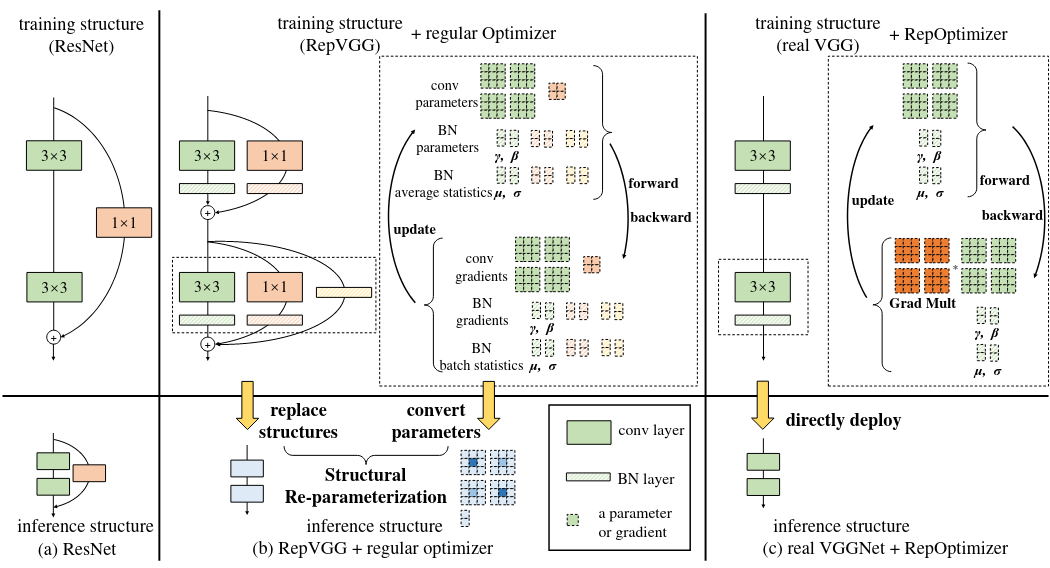
Rep-Optimizer hướng đến việc có một kiến trúc duy nhất trong training và testing. Như vậy, training cũng sẽ nhanh hơn và quantization cũng không gặp khó khăn gì. Ơ nhưng thế thì khác gì một model thông thường? Điểm khác biệt ở đây là, model sử dụng là VGG, sẽ có tốc độ training, tốc độ inference của VGG, nhưng accuracy thì của RepVGG (Hình 4).

Rep-Optimizer

Vậy làm như nào để có cái khả năng đề ra như mình nói ở phía trên? Thay vì tác động vào model, thì ta sẽ tác động vào gradient trong lúc training. Vì bản chất, khi training một model, ta sẽ sử dụng thông tin của gradient để cập nhật weight cho model đó. Ò ý tưởng thì có vẻ hiểu rồi, thế cách thực hiện thì như nào, làm thế nào để biết gradient cần phải thay đổi như nào? Để có thể hiểu được việc này, ta có quá trình 3 bước như sau: 1) Ta cần định nghĩa kiến thức ta mong muốn có được (prior knowledge) và kiến trúc mang kiến thức đó. 2) Ta cần định nghĩa kiến trúc ta hướng đến (target structure) trong quá trình test, để thay đổi gradient cho phù hợp. 3) Tính toán các hyper-params để tạo nên RepOptimizer. Vì vậy, chú ý là để có thể sử dụng được RepOptimizer, ta cần phải hiểu rõ:

• Target model: Model ta mong muốn sử dụng trong lúc inference (test time)
• Prior knowledge/Prior model: Model mà ta muốn target model của chúng ta đạt được accuracy như thế
• Cách backprop hoạt động: Mình nghĩ đây là bước khó nhất, cái này tùy thuộc vào trình độ toán học và ý chí của các bạn thôi :v

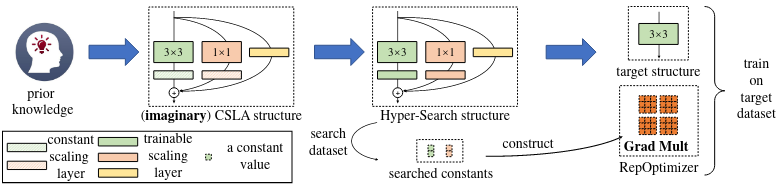
Định nghĩa Prior Knowledge

Bài này sẽ biểu diễn cách đưa kiến thức của RepVGG vào VGG. Trong RepVGG, kiến thức của nó chính là cộng inputs và outputs của các nhánh lại với nhau theo một hệ số scale. Cái kiến thức đơn giản đó đã được áp dụng trong rất nhiều model như: ResNet, sử dụng skip-connection để cộng input với output của nhánh residual. Trong trường hợp này, target model là VGG, prior model là RepVGG với block $3 \times 3$ Conv-BN, $1 \times 1$ Conv-BN và một nhánh mapping có BN.

Đưa prior knowledge vào Optimizer

Trước khi tìm hiểu về cách đưa prior knowledge của RepVGG vào Optimizer, ta xét tới hiện tượng sau: Ta xét một trường hợp đặc biệt khi mà toàn bộ các nhánh trong RepVGG Block chỉ bao gồm một trainable ops và có thể có thêm constant scale sau trainable ops (một hệ số nhân bất biến, dùn để nhân với output của trainable ops) thì độ chính xác của model vẫn rất cao nếu constant scale này có giá trị hợp lý. Và ta gọi block có dạng 3 nhánh, mỗi nhánh có 1 trainable ops (+ 1 constant scale) này là Constant Scale Linear Addition (CSLA) block (Hình 5). Nhóm tác giả nhận ra rằng ta có thể thay thế cái CSLA Block này bằng một trainable ops và từ đó rút ra equivalent training dynamic (mình cũng không biết dịch như nào cho hay). Equivalent training dynamic có nghĩa là: sau $T$ iteration, với input ở iteration $t$ của CSLA Block cũng giống với input ở iteration $t$ của một trainable ops, thì chúng luôn có một kết quả như nhau. Nếu văn nói của mình khó hiểu quá thì mời các bạn đọc tiếp phía dưới, có công thức toán học.

Equivalent training dynamic đạt được khi ta nhân gradient với một hệ số nhân được tìm ra từ constant scale. Ta gọi hệ số dùng để nhân với gradient đó là GradMult (Hình 5). Việc thay đổi gradients sử dụng GradMult có thể gọi là quá trình Re-params thực hiện trên gradient. Tóm lại:

$$\text{CSLA Block + Optimizer thông thường} = \text{Ops + Optimizer nhưng được Re-params}$$

Phần chứng minh cho điều vừa nói trên mình sẽ để ở phần phụ lục của bài viết này Oke bây giờ đến biểu diễn toán học một chút. Gọi $\alpha_A, \alpha_B$ là 2 hằng số. $W^{(A)}, W^{(B)}$ là 2 kernel của lớp Conv có cùng shape với nhau. $X$ là input và $Y$ là output. $*$ là phép Conv. CSLA Block được tính như sau:

$$Y_{CSLA} = \alpha_A(X * W^{(A)}) + \alpha_B(X * W^{(B)})$$

Còn khi sử dụng Optimizer được Re-params (GR), ta gọi kernel của ops đó là $W^{'}$, do đó:

$$Y_{GR} = X * W^{'}$$

Gọi $i$ là số training iteration, ta có thể có được $Y_{CSLA}^i = Y_{GR}^i$ khi và chỉ khi ta tuân thủ 2 luật:

• Luật khởi tạo (Rule of initialize): Kernel của ops ($W^{'}$) phải được khởi tạo như sau: $W^{'(0)} \leftarrow \alpha_A W^{(A) (0)} + \alpha_B W^{(B) (0)}$. Hay nói cách khác, kernel của ops phải được khởi tạo tương đương như của CSLA Block
• Luật update theo iteration: CSLA Block khi train với Optimizer thông thường thì update như thuông thường, còn khi sử dụng GR, gradient sẽ phải nhân với hệ số $(\alpha_A^2 + \alpha_B^2)$. Gọi $L$ là objective function, $\lambda$ là learning rate, ta sẽ update $W^{'}$ như sau:

$$W^{' (i+1)} \leftarrow W^{' (i)} - \lambda (\alpha_A^2 + \alpha_B^2) \frac{\partial L}{\partial W^{' (i)}}$$

Đã hiểu làm thế nào để $CSLA = GR$, ta sẽ thiết kế và mô tả RepOptimizer bằng việc thiết kế CSLA trước. Với việc áp dụng RepOptimizer lên VGG theo RepVGG (Gọi là RepOpt-VGG), CSLA sẽ được khởi tạo bằng việc thay thế lớp BN ở sau 2 lớp Conv $3 \times 3$ và $1 \times 1$ bằng một hằng số scale theo chiều channel (để hiểu rõ hơn mời các bạn đọc lại cách BN hoạt động như nào tại đây) , còn BN trong identity branch của RepVGG sẽ được thay bằng một tham số scale theo chiều channel (vì mỗi nhánh trên CSLA Block đều phải có một trainable ops). Tham số scale theo chiều channel này có thể hiểu là một lớp Depthwise Conv, lưu ý rằng đây là tham số scale theo chiều channel chứ không phải hằng số scale theo chiều channel (CSLA structure trên Hình 5)

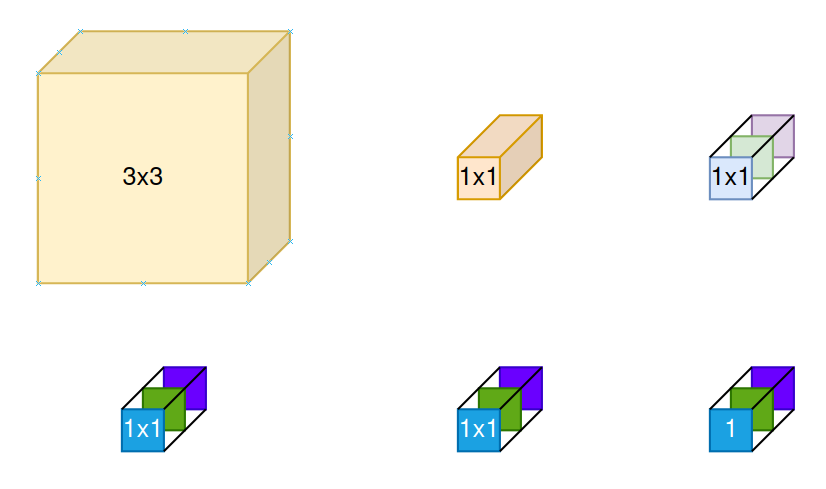
Xét một trường hợp phức tạp hơn, lớp Conv ở mỗi nhánh có kernel size khác nhau và ngay sau chúng là một hằng số scale theo chiều channel, GradMult lúc này sẽ là một tensor. Cách tính GradMult cho CSLA đại diện cho RepVGG, sẽ được sử dụng để training cho target block là $3 \times 3$ Conv như sau: Gọi $C$ là số channels, $s,t \in \R^C$ là hằng số scale theo chiều channel sau lớp $3 \times 3$ Conv và $1 \times 1$ Conv, GradMult $M^{C \times C \times 3 \times 3}$ sẽ được tính theo công thức sau:

$$M_{c,d,p,q} = \begin{cases} 1 + s^2_c + t^2_c & \text{nếu } c = d, p=2 \text{ và } q=2 \\ s^2_c + t^2_c & \text{nếu } c \neq d, p=2 \text{ và } q=2 \\ s^2_c & \text{còn lại} \end{cases}$$

$p=2$ và $q=2$ có nghĩa là điểm trung tâm của cái $3 \times 3$ kernel.

Oke giờ mình sẽ giải thích công thức trên rõ hơn một chút. Khuyến khích mọi người vừa đọc phần dưới đây vừa nhìn vào Hình 6

Nhìn lại khối CSLA Block đại diện cho 2 lớp Conv có cùng kernel size theo sau đó là 2 hằng số scale theo chiều channel $\alpha_A, \alpha_B$ ở tít phía trên, mình sẽ gọi là CSLA 1. GradMult của CSLA 1 $M_{c,d,p,q} = \alpha_A^2 + \alpha_B^2 \quad \forall c,d,p,q$. Nếu không hiểu phần này, hãy đọc ở phụ lục, còn chưa đọc phần phụ lục mà vẫn muốn hiểu cách tìm $M$ cho CSLA Block của RepVGG thì giờ hãy chấp nhận cách tìm $M$ cho CSLA 1.

Mở rộng CSLA 1 lên thành CLSA 2, là một kiến trúc có 2 nhánh, một nhánh là $3 \times 3$ Conv và nhánh còn lại là $1 \times 1$ Conv, theo sau mỗi lớp Conv lại là hằng số scale theo chiều channel $\alpha_A, \alpha_B$. Lúc này, $1 \times 1$ Conv sẽ được kết hợp với $3 \times 3$ Conv tại điểm trung tâm của $3 \times 3$ Conv. Do đó, GradMult của CSLA 2 sẽ như sau:

$$M_{c,d,p,q} = \begin{cases} \alpha_A^2 + \alpha_B^2 & \text{nếu } p=2, q=2 \\ \alpha_A^2 & \text{còn lại} \end{cases}$$

Thấy GradMult cho CSLA 2 có giống với 2 dòng cuối của GradMult cho CSLA RepVGG chưa nào :v

Còn vì tại sao GradMult cho CSLA RepVGG phải chia cả theo từng channel nữa là vì nguyên lý hoạt động của Depthwise Conv. CSLA RepVGG có một nhánh thứ 3 là $1 \times 1$ Depthwise Conv, và hằng số scale theo chiều channel lúc này sẽ bằng 1 tại toàn bộ các channel, do đó ta chỉ cần $+1$ tại $c=d$

Tìm các Hyper-params cho RepOptimizer thông qua Hyper-Search

Ở đầu phần trên, đã có nhận định là "Ta xét một trường hợp đặc biệt khi mà... (yada yada yada)... nếu constant scale này có giá trị hợp lý". Giờ ta phải tìm cái giá trị hợp lý cho constant scale này như nào? Vì Neural Network (NN) vốn là một cái hộp đen, nên tìm được giá trị chính xác cho constant scale này dường như là không thể, vì vậy ta sẽ xấp xỉ giá trị này, và phương pháp sắp tới đây sẽ gọi là Hyper-Search. Cụ thể, với một RepOptimizer, ta sẽ dựng một Hyper-Search model bằng việc thay toàn bộ constant scale thành trainable scale (tức là lấy lại nguyên cái RepVGG đấy). Và ta sẽ train cái Hyper-Search model này trên một cái dataset cỡ vừa (VD: CIFAR 100). Giá trị cuối cùng của trainable scale được train với bộ dataset cỡ vừa này sẽ được chuyển thành constant scale được sử dụng trong CSLA.

Training với RepOptimizer

Sau Hyper-Search, ta sẽ dùng constant scale vừa search được để tạo GradMult cho RepOptimizer của mỗi ops (với RepOpt-VGG thì các ops ở đây là $3 \times 3$ Conv). Trong lúc training, RepOptimizer sẽ thực hiện nhân gradients của từng ops với GradMult tương ứng của từng ops của mỗi lần forward/backward $\rightarrow$ Luật update theo iteration

Ta cũng phải tuân thủ Luật khởi tạo. Gọi $W^{(s)(0)} \in \R^{C \times C \times 3 \times 3}$ và $W^{(t)(0)} \in \R^{C \times C \times 1 \times 1}$ là weight được khởi tạo của $3 \times 3$ Conv và $1 \times 1$ Conv của CSLA RepVGG. Do đó, weight của RepOpt-VGG được khởi tạo như sau:

$$W_{c,d,p,q}^{'(0)} = \begin{cases} 1 + s_c W_{c,d,p,q}^{(s)(0)}+ t_c W_{c,d,1,1}^{(t)(0)} & \text{nếu } c = d, p=2 \text{ và } q=2 \\ s_c W_{c,d,p,q}^{(s)(0)} + t_c W_{c,d,1,1}^{(t)(0)} & \text{nếu } c \neq d, p=2 \text{ và } q=2 \\ s_c W_{c,d,p,q}^{(s)(0)} & \text{còn lại} \end{cases}$$

Kết quả so sánh với RepVGG trên ImageNet

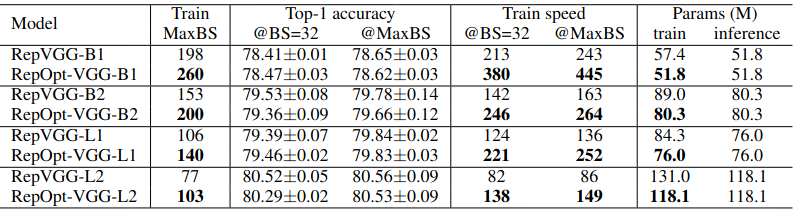
Phụ lục

Chứng minh CSLA = GR

Yêu cầu chuẩn bị sẵn kiến thức về toán cao cấp, lấy giấy bút ra, và suy ngẫm nếu bạn muốn hiểu phần này, còn nếu bạn pro không cần giấy bút thì xin chúc mừng.
CSLA là một block mà mỗi nhánh ở trên mỗi block đó có một trainable ops và theo sau là một constant scale. Chứng minh rằng, training một CSLA block với Optimizer thông thường sẽ như là training một trainable ops với gradient được sửa đổi

Xét trường hợp CSLA Block có 2 nhánh, mỗi nhánh có 1 lớp Conv với kernel size của lớp Conv trên các nhanh là như nhau, theo sau mỗi lớp Conv là một hằng số scale theo chiều channel. Gọi $\alpha_A, \alpha_B$ là 2 hằng số scale, $W^{(A)}, W^{(B)}$ là kernel của mỗi lớp Conv. Gọi $X$ là input và $Y$ là output, $Y_{CSLA} = \alpha_A (X * W^{(A)}) + \alpha (X * W^{(B)})$ với * là phép conv. Khi sử dụng Gradient Re-params (GR), ta sẽ train target model theo weight $W^{'}$, với $Y_{GR} = X * W^{'}$. Gọi objective function là $L$, số training iteration là $i$, gradient của một kernel $W$ là $\frac{\partial L}{\partial W}$, $F(\frac{\partial L}{\partial W^{'}})$ là áp dụng biến đổi $F$ lên gradient của kernel của GR $W^{'}$.

Phát biểu: Tồn tại một phép biến đổi $F$ theo $\alpha_A$ và $\alpha_B$ sao cho khi update $W^{'}$ theo $F(\frac{\partial L}{\partial W^{'}})$ sẽ đảm bảo được rằng:

$$Y_{CSLA}^{(i)} = Y_{GR}^{(i)} \quad \forall i \geq 0 \quad (1)$$

Chứng minh: Để $(1)$ đúng, ta cần phải có:

$$\alpha_A W^{(A)(i)} + \alpha_B W^{(B)(i)} = W^{'(i)} \quad \forall i \geq 0 \quad (2)$$

Tại iteration $0$, chỉ cần initialize đúng là đã thỏa mãn phương trình $(2)$. Giả dụ $W^{(A)(0)}, W^{(B)(0)}$ là giá trị initialize của kernel trong CSLA Block, thì điều kiện ban đầu:

$$W^{'(0)} = \alpha_A W^{(A)(0)} + \alpha_B W^{(B)(0)}$$

để:

$$Y_{CSLA}^{(0} = Y_{GR}^{(0)} \rightarrow \text{luật khởi tạo}$$

Giờ ta sẽ chứng minh, bằng việc thay đổi gradient của $W^{'}$, thì ta sẽ luôn có được sự tương đồng: $Y_{CSLA}^{(i)} = Y_{GR}^{(i)}$. Gọi $\lambda$ là learning rate, theo update rule có:

$$W^{(i+1)} = W^{(i)} - \lambda \frac{\partial L}{\partial W^{(i)}}$$

Áp dụng update rule lên CSLA Block, ta có:

$$\alpha_A W^{(A)(i+1)} + \alpha_B W^{(B)(i+1)} = \alpha_A W^{(A)(i)} + \alpha_B W^{(B)(i)} - \lambda (\alpha_A \frac{\partial L}{\partial W^{(A)(i)}} + \alpha_B \frac{\partial L}{\partial W^{(B)(i)}}) \quad (3)$$

Nếu ta sử dụng $F(\frac{\partial L}{\partial W^{'}})$ để update $W^{'}$ theo update rule, ta có:

$$W^{' (i+1)} = W^{'(i)} - \lambda F(\frac{\partial L}{\partial W^{'(i)}}) \quad (4)$$

Từ $(2), (3), (4)$, ta có:

$$F(\frac{\partial L}{\partial W^{'(i)}}) = \alpha_A \frac{\partial L}{\partial W^{(A)(i)}} + \alpha_B \frac{\partial L}{\partial W^{(B)(i)}} \quad (5)$$

Đạo hàm từng phần $(2)$, ta có:

$$\frac{\partial W^{'(i)}}{\partial W^{(A)(i)}} = \alpha_A, \quad \frac{\partial W^{'(i)}}{\partial W^{(B)(i)}} = \alpha_B \quad (6)$$

Từ $(5)$ và $(6)$, ta có:

$$F(\frac{\partial L}{\partial W^{'(i)}}) = \alpha_A \frac{\partial L}{\partial W^{'(i)}} \frac{\partial W^{'(i)}}{\partial W^{(A)(i)}} + \alpha_B \frac{\partial L}{\partial W^{'(i)}} \frac{\partial W^{'(i)}}{\partial W^{(B)(i)}}$$

Hay:

$$F(\frac{\partial L}{\partial W^{'(i)}}) = (\alpha_A^2 + \alpha_B^2) \frac{\partial L}{\partial W^{'(i)}} \quad (7)$$

Với $(7)$, ta đảm bảo được rằng $\alpha_A W^{(A)(i+1)} + \alpha_B W^{(B)(i+1)} = W^{'(i+1)}$ nếu $\alpha_A W^{(A)(i)} + \alpha_B W^{(B)(i)} = W^{'(i)}$. Do đó, kết hợp luật khởi tạo với luật update iteration đã được chứng minh thông qua $(7)$, ta có thể thấy tồn tại một hệ số nhân thay đổi gradient theo $\alpha_A, \alpha_B$ để đạt sự tương đồng trong output giữa 2 kiến trúc khác nhau: CSLA Block và $3 \times 3$ Conv

Reference

Re-parameterizing Your Optimizers rather than Architectures: https://arxiv.org/abs/2205.15242