I. Giới thiệu

VGG - mô hình học sâu được đề xuất bởi K. Simonyan and A. Zisserman trong bài báo Very Deep Convolutional Networks for Large-Scale Image Recognition”. Khi xuất hiện mô hình này đã nhanh chóng chứng tỏ sức mạnh của mình vượt qua mô hình sota trước đó là AlexNet trên tập ImageNet. Tuy nhiên về sau khi các mô hình ngày càng phát triển sâu hơn phức tạp hơn, VGG đã lộ ra rất nhiều điểm yếu của mình và bị bỏ xa so với những mô hình như ResNet, Inception, EfficientNet, ... Cũng từ rất lâu rồi, cá nhân mình cũng đã không dùng VGG trong các bài toán machine learning nữa vì những nhược điểm đó. Nhưng có lẽ thời gian tới mình có thể thay đổi vì màn comeback vô cùng ấn tượng dưới cái tên hoàn toàn mới RepVGG

RepVGG là một kiến trúc đơn giản nhưng mạnh mẽ có phần inference time body giống như VGG chỉ bao gồm các convolution 3x3, Relu trong khi phần mô hình lúc huấn luyện lại có kiến trúc đa nhánh giống các mô hình họ Resnet. Đọc đến đây mình cũng tự hỏi "Ủa lúc huấn luyện thì lại giống Resnet, inference lại giống VGG ? Thế thì dùng kiểu gì nhỉ ???". Về sau đọc paper mới biết, tác giả làm được như vậy bằng kỹ thuật re-parameterization, tiếng Việt mình search trên google là "tham số hóa lại" hơi khó hiểu nhể ? Nhưng nói chung nó là kỹ thuật biến đổi một tập tham số từ kiến trúc này sang kiến trúc khác nên dù hai kiến trúc khác bọt hẳn nhưng nó vẫn share được weight cho nhau. Và đó cũng là lý do cho cái tên RepVGG này (Re-parameterization VGG). Còn cụ thể nó re-parameterization như nào thì mình sẽ giải thích cụ thể sau nhé.

II. Kiến trúc của RepVGG

Giống như EfficienetNet, RepVGG cũng có một họ các anh em cùng loại với nó như RepVGG-A0, RepVGG-A1,... Tuy nhiên chúng đều có đặc điểm chung như sau:

• Kiến trúc được tách thành hai phần riêng biệt đơn nhánh khi inference và đa nhánh khi training.
• Mô hình gồm có 5 stages. Tất cả các block đầu tiên mỗi stage đều có stride bằng 2, các block khác thì có stride bằng 1.
• Mô hình chỉ sử dụng convolution có kernel 3x3 và Relu (nhánh identity và 1x1 chỉ dùng khi training), loại bỏ hoàn toàn lớp pooling trong VGG.
• Thiết kế đơn giản không dùng các thiết kế như automatic search trong efficientnet hay các thiết kế nặng nề khác.

Thật là thử thách khi chỉ dùng một mô hình đơn giản không đao to búa lớn như VGG mà có thể đạt độ chính xác của những mô hình to lớn hơn nó rất nhiều. Nào bây giờ mình cùng phân tích các đặc trưng của mô hình để xem điều gì đã khiến một mô hình đơn giản trở nên mạnh mẽ đến như vậy

1. Đơn nhánh và đa nhánh

1.1. Tại sao chúng ta cần mô hình đa nhánh ?

Các nghiên cứu trước đó đã chỉ ra rằng các mô hình có rất nhiều lớp (deep model) tuy tốt không thể có độ chính xác vượt các mô hình phức tạp (complicated model). Đã có một mô hình 10000 lớp thuần được huấn luyện đạt độ chính xác 99% trên tập MNIST và 82% trên tập CIFAR-10. Tuy nhiên mô hình như vậy không hiệu quả bởi vì chỉ cần những mô hình đơn giản như LeNet-5 cũng có thể đạt 99.3% trên tập MNIST và VGG-16 đạt độ chính xác 93% trên CIFAR-10. Điều này đã cho thấy không phải mô hình cứ sâu cứ nhiều lớp là sẽ tốt. Và thiết kế đa nhánh ở đây cùng với skip connection sẽ làm mô hình trở nên phức tạp hơn, tăng cường việc học các đặc trưng và tránh được hiện tượng gradient bị biến mất (vanishing gradient)

Chúng ta có thể nhìn thấy kiến trúc đa nhánh xuất hiện rất nhiều trong các mô hình hiện đại như Resnet18/34/50, EfficientNet B0-B7,... Và thực nghiệm đã chứng minh những mô hình đa nhánh như vậy dễ dàng hội tụ hơn cũng như đạt hiệu quả tốt hơn so với những mô hình đơn nhánh. Có một lý do khác giải thích cho sự hiệu quả này là kiến trúc đa nhánh làm mô hình ban đầu là biểu diễn của rất nhiều các mô hình bé (shallow model). Với n block thì mô hình có thể gồm $2^{n}$ mô hình con vì mỗi block sẽ được chia làm 2 nhánh. Điều này khiến mô hình trở nên tổng quát hơn không phụ thuộc vào bất cứ lớp nào. Mô hình có nhiều đường độc lập thay vì một đường như VGG.Bạn có thể một vài lớp bất kì trong Resnet và có thể quan sát thấy performance sẽ không thay đổi đáng kể nhưng bạn làm điều tương tự với kiến trúc VGG performance sẽ trở nên rất tệ.

Mỗi khối trong kiến trúc RepVGG gồm ba nhánh 3x3, 1x1 và identity. Nếu trong RepVGG có n block như thế thì trong mô hình có tổng cộng $3^n$ mô hình con nhờ đó mô hình trở nên phức tạp hơn, tổng quát hơn cũng có nghĩa sẽ biểu diễn tốt hơn theo lý thuyết.

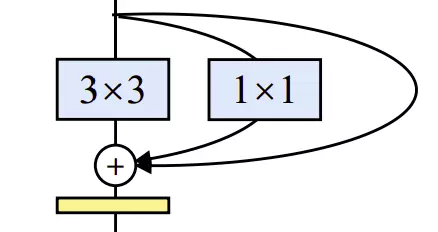RepVGG Block

1.2. Còn kiến trúc đơn nhánh thì sao ?

Đa nhánh sẽ giúp mô hình chúng ta dễ hội tụ hơn và đạt độ chính xác cao hơn. Nhưng những ưu điểm đó chỉ phát huy tác dụng trong quá trình huấn luyện. Còn khi dùng để inference thì nó lại có một số nhược điểm.

Thứ nhất tốc độ: Nhiều mô hình đa nhánh có FLOPS thấp hơn mô hình VGG rất nhiều nhưng thực tế khi inference lại không nhanh bằng. Ví dụ như VGG-16 có FLOPS gấp 8.4 lần so với mô hình Efficientnet B3 nhưng VGG-16 lại chạy nhanh gấp 1.8 lần trên 1080Ti. Điều đó chứng tỏ FLOPS không phản ánh tất cả yếu tố đóng góp vào tốc độ của một mô hình (Chú ý: theo wikipedia FLOPS là thước đo hiệu suất máy tính thể hiện số phép tính trong một giây.). Có hai yếu tố ảnh hưởng rất nhiều đến tốc độ tuy nhiên không thể hiện trong FLOPS đó là:

• Chi phí truy cập bộ nhớ (memory access cost)
• Mức độ tính toán song song hóa (degree of parallelism)

Trong trường hợp kiến trúc đa nhánh, thời gian tính toán cho các lớp như cộng hay ghép nối giữa các nhánh không đáng kể tuy nhiên thời gian truy cấp bộ nhớ lại khá đáng kể đồng thời khả năng song song hóa của kiến trúc đa nhánh cũng kém hơn kiến trúc đơn nhánh do đó kể cả có FLOPS lớn hơn nhưng các mô hình đơn nhánh lại nhanh hơn rất nhiều

Thứ hai chi phí bộ nhớ: Kiến trúc đa nhánh không hiệu quả trong sử dụng bộ nhớ vì kết quả của tất cả các nhánh phải được giữ lại cho đến khi thực hiện cộng hoặc ghép các nhánh đó vào làm một. Trong khi đối với kiến trúc đơn nhánh thì bộ nhớ lập tức được giải phóng khi tính toán xong do đó tối ưu được chi phí sử dụng bộ nhớ. Vấn đề liên quan đến chi phí bộ nhớ khá quan trọng trong việc triển khai các mô hình machine learning xuống các thiết bị nhỏ như mobile hay các hệ thống nhúng.

Thứ ba là linh hoạt: Cấu trúc đa nhánh thường kém linh hoạt hơn trong việc thiết kế kiến trúc mô hình. Ví dụ như ResNet yêu cầu các khối tích chập phải tổ chức như các khối residual để lớp cuối cùng trong một khối luôn có các tensor cùng kích thước để có thể cộng hoặc ghép nối các nhánh vào với nhau.

1.3 Kết hợp cả hai kiến trúc.

Sau khi phân tích các lý do bên trên ta có thể chốt lại là: kiến trúc đa nhánh thì có những điểm tốt cho huấn luyện còn kiến trúc đơn nhánh lại có những điểm tốt cho inference. Từng kiểu lại có cái hay riêng của nó.

Do hai kiến trúc này khác nhau nên để có thể sử dụng tất cả ưu điểm của cả kiến trúc này thì cần đến một kĩ thuật để chuyển đổi các tham số của mô hình này sang mô hình khác. Đây cũng là kỹ thuật chính tạo nên sự khác biệt cho mô hình Re-parameterization.

Khi huấn luyện, một block của RepVGG sẽ có ba nhánh gồm các convolution có kernel 3x3, 1x1 và nhánh identity. Khi inference, một block RepVGG chỉ có 1 convolution 3x3. Tất cả sau lớp conv 3x3, 1x1 hay identity tác giả đều dùng thêm lớp batch normalization. Và đây là cách tác giả chuyển tham số của mô hình khi huấn luyện sang inference.

Đây là một số chú thích một số ký hiệu toán học sẽ được sử dụng trong bài :

• $C_1:$ input channel
• $C_2$: output channel
• $M^{(1)} ∈ R^{N × C_1 × H_1 × W_1}$: input
• $M^{(2)} ∈ R^{N × C_2 × H_2 × W_2}$: output
• $W^{(3)} ∈ R^{C_2 × C_1 × 3 × 3}$: kernel của conv 3x3
• $W^{(1)} ∈ R^{C_2 × C_1}$: kernel của conv 1x1
• $\mu^{(3)}, \sigma^{(3)}, \gamma^{(3)}, \beta^{(3)}$: mean, stanndard deviation, scalling factor và bias của lớp Batch Norm sau lớp conv 3x3
• $\mu^{(1)}, \sigma^{(1)}, \gamma^{(1)}, \beta^{(1)}$: mean, stanndard deviation, scalling factor và bias của lớp Batch Norm sau lớp conv 1x1
• $\mu^{(0)}, \sigma^{(0)}, \gamma^{(0)}, \beta^{(0)}$: mean, stanndard deviation, scalling factor và bias của lớp Batch Norm của nhánh identity
• $*$: phép tích chập
• bn: lớp batch normalization

Khi inference, batch normalization được tính như sau:

Với $∀1 ≤ i ≤ C_2$

$bn(M, \mu, \sigma, \gamma, \beta)_{:, i, :, :} = (M_{:, i, :, :} - \mu_i) \frac{\gamma_i}{\sigma_i} + \beta_i$ = $M_{:, i, :, :}\frac{\gamma_i}{\sigma_i} + (- \mu_i\frac{\gamma_i}{\sigma_i} + \beta_i)$

Đặt $W'_{i, :, :, :} = \frac{\gamma_i}{\sigma_i} W_{i, :, :, :}$, $b'_i = -\frac{\mu_i\gamma_i}{\sigma_i} + \beta_i$

Ta có:

$M^{(2)} = bn(M * W, \mu, \sigma, \gamma, \beta)_{:, i, :, :} = (M_{:, i, :, :} W_{:, i, :, :}- \mu_i) \frac{\gamma_i}{\sigma_i} + \beta_i = (M^{(1)} * W')_{:, i, :, :} + b'_i = M^{(1)} * W' + b'$

Khi huấn luyện, output của RepVGG block sẽ được tính như sau :

$M^{(2)} = bn(M^{(1)} * W^{(3)}, \mu^{(3)}, \sigma^{(3)}, \gamma^{(3)}, \beta^{(3)}) + bn(M^{(1)} * W^{(1)}, \mu^{(1)}, \sigma^{(1)}, \gamma^{(1)}, \beta^{(1)}) + bn(M^{(1)}, \mu^{(0)}, \sigma^{(0)}, \gamma^{(0)}, \beta^{(0)})$

$M^{(2)} = (M^{(1)} * W'^{(3)})_{:, i, :, :} + b'^{(3)}_i + (M^{(1)} * W'^{(1)})_{:, i, :, :} + b'^{(1)}_i + (M^{(1)} * W'^{(0)})_{:, i, :, :} + b'^{(0)}_i$

$M^{(2)} = M^{(1)} * (W'^{(1)} + W'^{(3)} + W'^{(0)}) + (b'^{(0)} + b'^{(3)} + b'^{(1)})$

Để chuyển tham số giữa hai kiến trúc đơn nhánh và đa nhánh thì batch normalization giữa hai kiến trúc đa nhánh và đơn nhánh phải tương ứng với nhau do đó kích thước của $W'^{(1)}, W'^{(3)}, W'^{(0)}$ phải giống nhau để có thể thực hiện phép cộng tương ứng. Do $W'^{(1)}, W'^{(3)}, W'^{(0)}$ có kích thước lần lượt là 1x1, 3x3, 1x1 để cùng kích thước cần phải padding các giá trị 0 vào $W'^{(1)}, W'^{(0)}$ cùng kích thước với $W'^{(3)}$.

Cuối cùng, ta có:

Khi huấn luyện: $M^{(2)} = M^{(1)} * W'^{(1 + 3 + 0)} + b'^{(1 + 3 + 0)}$

Khi inference: $M^{(2)} = M^{(1)} * W' + b'$

==> $M^{(1)} = W'^{(1 + 3 + 0)}$ và $b' = b'^{(1 + 3 + 0)}$

Yup vậy ta hoàn toàn chuyển thành công tham số từ kiến trúc đa nhánh về đơn nhánh rồi

2. Winograd Convolution

Như phần trên mình cũng đã đề cập, RepVGG chỉ sử dụng kernel 3x3 bởi vì kernel kích thước 3x3 được tối ưu bởi rất nhiều thư viện tính toán hiện đại như NVIDIA cuDNN và Intel MKL trên GPU và CPU. Theo so sánh trên có thể thấy về mặt lý thuyết FLOPS của kernel 3x3 gấp nhiều lần so với kernel khác. Tuy nhiên cũng như phần trên mình đã chỉ ra FLOPS không phản ánh hoàn toàn thời gian tính toán thực tế . Do thực hiện phép nhân tốn thời gian rất nhiều hơn phép cộng, nên ta đếm số phép nhân để ước tính chi phí tính toán convolution.

Winograd là một thuật toán có thể tối ưu tính toán của convolution 3x3 được hỗ trợ tại nhiều thư viện như cuDNN hay MKL. Nhờ Winograd số phép nhân cần tính toán trên kernel 3x3 giảm còn 4/9 so với ban đầu nhờ đó tốc độ tính toán nhanh hơn rất nhiều so với việc sử dụng kernel 5x5 hay 7x7. Đồng nghĩa nhờ chỉ việc sử dụng kernel 3x3, RepVGG đã tăng tốc độ đáng kể cho mô hình.

III. Lời kết

Bài viết cũng tương đối dài và cũng có nhiều phần công thức toán hy vọng không làm các bạn nhàm chán. Nhưng việc áp dụng kỹ thuật tham số hóa hay re-parameterization vào một mô hình đơn giản như VGG để so sánh với các mô hình phức tạp như Efficienet kiến trúc phức tạp đồng thời thời gian xử lý được giảm đi rất nhiều quả thật là một ý tưởng hết sức thú vị. Cảm ơn các bạn đã theo dõi bài đọc của mình. Phần áp dụng mô hình trong bài toán thực tế mình sẽ hoàn thiện trong thời gian gần nhất. Hy vọng các bạn sẽ đón xem.

Tham khảo:

• RepVGG: Making VGG-style ConvNets Great Again