Tính chất của Self-Attention và Transformer trong Computer Vision
Bài đăng này đã không được cập nhật trong 3 năm
Mở đầu
Qua 2 bài viết: cơ chế Attention trong Computer Vision và MetaFormer với cái tiêu đề đầy chế giễu, thì giống như mình là một hater của Self-Attention. Thì đúng là mình có một chút gì đó không thích Self-Attention thật (vì nó nặng, và mình thì thích những thứ gì nhanh và nhẹ) nhưng dù sao thì mình vẫn phải tìm hiểu nó thôi :v
Nên là hôm này mình sẽ trình bày một chút kiến thức của mình về Self-Attention trong Computer Vision. Đây không phải là một bài Paper Explain nên mình sẽ không đi quá sâu vào chứng minh những gì được nhắc tới trong bài này. Đây sẽ chỉ là bài tổng hợp kiến thức thôi, nên nếu muốn hiểu sâu về chứng minh thì độc giả có thể đọc những paper mình để ở trong Reference. Vì bài này có khá nhiều toán, và mình thì rất kém toán, nên nếu có sai sót gì mong các bạn có thể chỉ ra cho mình.
Yêu cầu nho nhỏ
Trước khi đọc bài viết này, các bạn nên hiểu một số thứ như: Attention là gì, Self-Attention là gì, phép toán và ý tưởng của Self-Attention, Self-Attention được áp dụng vào ảnh như nào, các model áp dụng Self-Attention qua thời gian.
Viết tắt:
- MSAs: Multi-head Self Attention(s)
- Convs: Convolution(s)
- NN: Neural Network
- ViT: Vision Transformer
- FC: Fully Connected
- GAP: Global Average Pooling
Nội dung
Bài này sẽ tập trung vào trả lời 3 câu hỏi:
- Tính chất gì của MSAs là cần thiết cho việc tối ưu NN một cách tốt hơn? Liệu rằng có phải là do khả năng học long-range dependency (khả năng phụ thuộc xa) của nó?
- MSAs có hoạt động giống như Convs? Nếu không thì chúng khác nhau như thế nào?
- Ta có thể kết hợp MSAs với Convs được không?
Tính chất gì của MSAs là cần thiết cho việc tối ưu NN tốt hơn?
Để hiểu được bản chất của MSAs, ta sẽ khám phá các đặc trưng của họ model ViT: như vanilla ViT (ViT thuần), PiT (Multi-stage ViT) và Swin (ViT + Multi-stage + local MSA). Để so sánh ViT với CNN, ta lấy ResNet làm đại diện cho phía CNN. Cả 2 loại model được train với training style trong DeiT. Như chúng ta thấy thì, ViT, hay chính xác hơn, các model thuần Attention, thì có inductive bias yếu nên thường phải sử dụng cực cực nhiều data để model có kết quả tốt. Vì vậy, CNN thường mang lại kết quả tốt hơn ViT khi được train với tập dataset nhỏ. Các bạn có thể đọc phần phụ lục để hiểu Inductive bias là gì
Inductive bias càng mạnh, thì khả năng biểu diễn càng mạnh (không phải regularization). Với tính inductive bias yếu, ViT thường có kết quả tệ trên tập test. Nhiều người cho rằng tính inductive bias mạnh sẽ hoạt động như một dạng regularization (cái mà các bạn hay nghe là L1 L2 regularization để chống overfit ý). Tức là, tính inductive bias yếu thì sẽ cực dễ bị overfit? Để trả lời câu hỏi này, ta train 2 dạng model, ViT và CNN, và sử dụng 2 chỉ số: (Negative Log Likelihood trong training, chỉ số này càng thấp thì càng tốt) và test error (càng thấp càng tốt). Tập dataset được sử dụng là CIFAR-100.
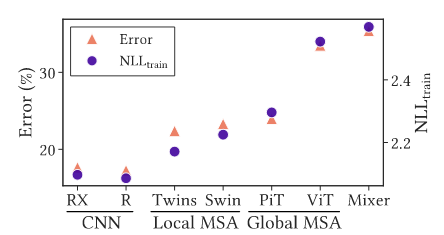
Nhìn vào kết quả ở Hình 1, ta có thể thấy tính inductive bias càng mạnh thì cả và Test error đều thấp. Điều này chứng tỏ tính inductive bias giúp model có khả năng biểu diễn tốt hơn chứ không hề chỉ có tác dụng regularization. Nếu inductive bias chỉ có tác dụng regularization, thì sẽ phải cao và Test Error sẽ thấp. Vì vậy, những model ViT được thêm inductive bias (local constraint) như Swin sẽ có kết quả tốt hơn ViT thuần là do chúng có khả năng biểu diễn tốt hơn.
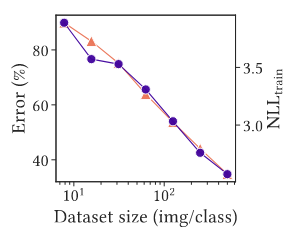
ViT không hề overfit trên tập dataset có ít dữ liệu. ViT thường phải train với một tập dữ liệu khổng lồ, và mọi người thường nghĩ rằng nó sẽ overfit nếu tập dữ liệu của ta nhỏ. Tuy nhiên sự thật thì lại không phải như thế. Kết quả ở Hình 2 đã cho ta thấy, khi số lượng samples trong dataset ít đi, Test Error tăng lên (không lạ) tuy nhiên cũng tăng lên. Nếu ViT overfit với dataset nhỏ, thì khi số lượng samples trong dataset ít đi, sẽ phải giảm xuống Điều này chứng tỏ kết quả của ViT tệ khi sử dụng dataset nhỏ không phải là do overfit.
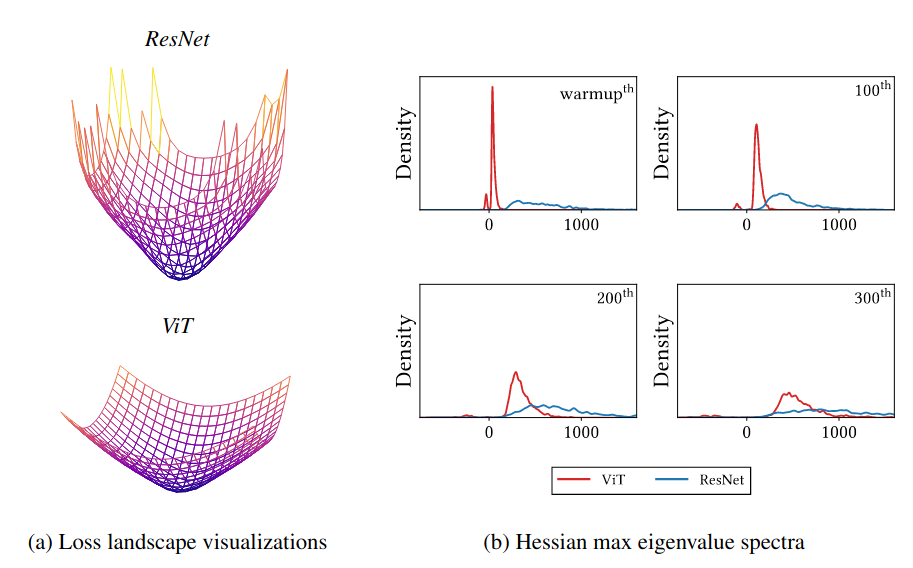
Hàm Loss của ViT không có dạng convex dẫn tới việc kết quả không tốt. Vậy inductive bias yếu thì ảnh hưởng như thế nào tới việc tối ưu? Nhìn vào Hessian eigenvalue của 2 loại model (Hình 3), ta sẽ thấy được sự ảnh hưởng.
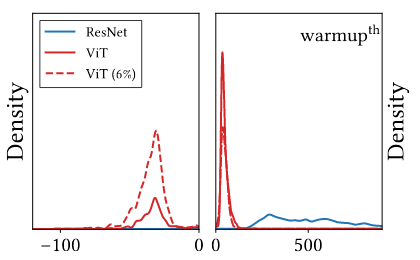
Từ hình 3, ta có thể suy ra Loss của ViT không có dạng convex còn của Resnet thì có dạng gần như là convex: Trong quá trình warmup, ViT có mật độ Hessian eigenvalue âm lớn, trong khi ResNet thì có rất ít. Bề mặt Loss như vậy (không convex) sẽ có sự ảnh hưởng tệ đến training, đặc biệt là vào những giai đoạn đầu của training. Hơn nữa, với dataset lớn thì mật độ Hessian eigenvalue âm của ViT được giảm đi đáng kể. Do đó, dataset lớn sẽ giúp bề mặt Loss của ViT convex hơn, dẫn đến kết quả test tốt hơn. Để hiểu rõ hơn về Hessian eigenvalue thì các bạn có thể đọc phần phụ lục của bài này.
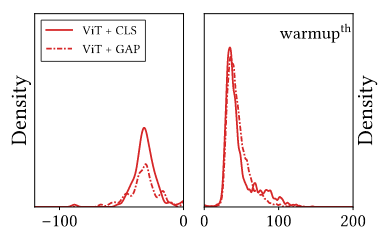
Các phương pháp làm smooth Loss sẽ giúp trong việc training ViT. Sử dụng các phương pháp làm smooth bề mặt Loss sẽ giúp ViT học được sự biểu diễn mạnh mẽ hơn. Trong bài toán phân loại ảnh, sử dụng GAP có thể smooth bề mặt Loss. Tương tự, ta có thể thay token trong ViT bằng cách sử dụng GAP classifier. Nhìn vào Hình 6, ta có thể thấy sử dụng GAP Classifier trong ViT sẽ giảm độ lớn Hessian eigenvalue âm, do đó, GAP giúp bề mặt Loss trở nên convex hơn. Tương tự, các phương pháp làm smooth khác như SAM, mà senpai team mình đã có một bài về nó ở đây, cũng giúp ViT trở nên tốt hơn.
MSAs làm mượt bề mặt Loss. MSAs có thể làm giảm độ lớn của Hessian eigenvalue. Nhìn vào Hình 5b, ta có thể thấy ViT có Hessian eigenvalue bé hơn rất nhiều so với CNN. Với Hessian eigenvalue lớn, CNN sẽ gặp khó khăn trong quá trình tối ưu. Ở phía trên mình có nói, bề mặt Loss của CNN có dạng gần convex, dẫn đến việc tối ưu dễ hơn là bề mặt Loss của ViT. Nhưng tại sao ở đây lại nói rằng CNN sẽ gặp khó khăn trong quá trình tối ưu. Đây là sự bổ sung cho phía bên trên. Ở trên mình chỉ nói rằng bề mặt Loss của CNN convex hơn của ViT, chứ không hề nói rằng CNN tối ưu tốt hơn ViT. CNN có bề mặt Loss convex hơn nhưng độ dốc của nó lại quá lớn, dẫn tới quá trình tối ưu gặp nhiều khó khăn, dẫn tới khả năng biểu diễn của CNN kém hơn. MSAs đã làm cho model học được khả năng biểu diễn mạnh hơn. Vậy là mỗi thứ đều có một điểm mạnh và điểm yếu của riêng nó.
Điểm quan trọng của MSAs là khả năng học đặc thù của data chứ không phải là khả năng phụ thuộc xa. MSAs có 2 thứ tạo nên sự đặc biệt của nó: long-range dependency (khả năng phụ thuộc xa) và data specificity (sự đặc thù của data). Hầu hết mọi người đều cho rằng, MSAs tốt hơn Convolution vì nó có khả năng nhìn được toàn bộ mọi thứ trên một tấm ảnh (long-range dependency), và mình nghĩ rằng MSAs được tạo ra cũng vì mục đích này, để thay thế RNN (mình có rất ít kiến thức của NLP nên nếu sai thì các bạn có thể comment sửa lại cho mình nhé). Tuy nhiên, tác giả đã làm thử thí nghiệm với convolution ViT (CSANs). CSANs chỉ tính toán Self-Attention giữa một số điểm trên feature maps như kiểu Convolution. Kết quả ở Hình 6
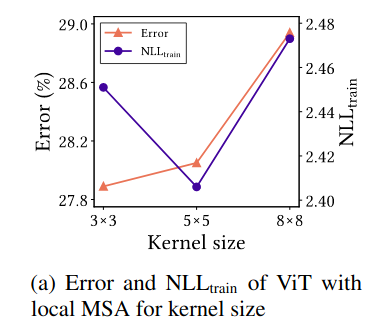
Ta có thể thấy, khi sử dụng kernel size lớn (), cả và cả Test error đều tăng, kết quả thu được giống với Hình 1 về tính inductive bias. Vậy, (too) long-range dependency sẽ làm giảm khá năng tối ưu của model, hay, locality giúp model học được sự biểu diễn tốt hơn (cả lẫn Test Error đều thấp). Tuy nhiên, khi sử dụng kernel size quá nhỏ () có cao hơn so với , tuy nhiên nó vẫn thấp hơn so với . Dù không thể hiện trong Hình 5, nhưng kết quả của CSANs với kernel khi test trên tập dataset CIFAR-100-C tốt hơn , tức là nó robust hơn. Điều này chưa có lời giải thích cụ thể, tác giả chỉ cho rằng việc quá local sẽ làm hại cho NN.
(too) long-range dependency sẽ làm giảm khả năng biểu diễn của model, dẫn đến hiệu năng kém, và (too) local cũng không hề tốt.
Một điểm nữa chứng minh rằng điểm quan trọng của MSAs là data specificity đó chính là: với model MLP-Mixer cũng có long-range dependency tuy nhiên nó vẫn yếu hơn các model ViT vì thiếu data specificity.
MSAs hành xử khác như nào so với Convs?
Convs là data-agnostic (không quan tâm đến data) và channel specific (đặc thù của channel) vì chúng mix thông tin của channel với nhau mà không khai thác thông tin về data. MSAs ngược lại, data specific và channel agnostic
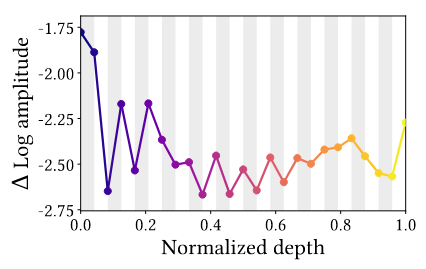
MSAs là bộ lọc thông thấp (low-pass filters), Convs là bộ lọc thông cao (high-pass filters). Hình 7 biểu diễn biên độ log tương đối của feature maps từ ViT qua biến đổi Fourier tại tần số cao (). Ta có thể thấy trên hình 7, MSAs hầu như luôn giảm biên độ của tần số, chỉ có ở đoạn đầu là nó tăng biên độ điều này cho ta gợi ý về một model kết hợp giữa Convs và MSAs với Convs ở phần đầu của model.
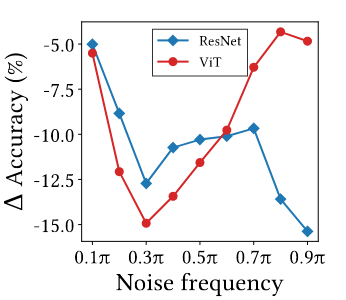
Tác giả còn làm thêm một thử nghiệm nữa: đo xem accuracy giảm như nào khi thêm random noise với tần số vào data: với là clean data, và là biến đổi Fourier thuận và nghịch, là noise và là mask mang tần số. Nhìn vào Hình 8, ta có thể thấy ViT nhạy cảm với nhiễu có tần số thấp (vì MSAs là bộ lọc thông thấp) còn Convs thì nhảy cảm với tần số cao (Convs là bộ lọc thông cao)
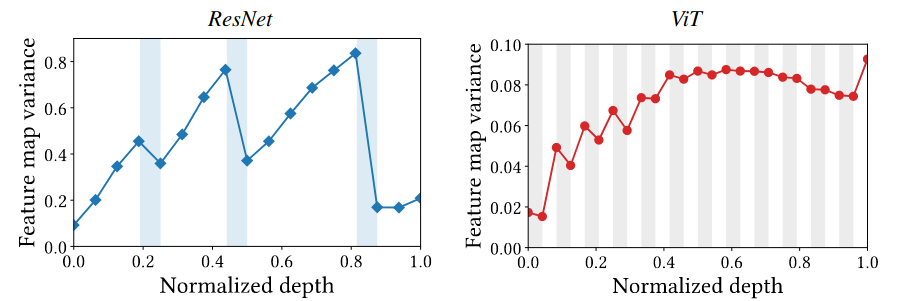
MSAs tổng hợp feature maps, còn Convs thì không. Vì MSAs thực hiện average feature maps (tính chất của softmax trong MSAs), nên sẽ làm giảm variance của từng điểm trong feature maps.
Tích hợp MSAs vào CNN
Với những kết luận nói trên, tác giả tạo ra một cách để tích hợp MSAs vào một CNN. Luật tích hợp như sau:
- Thay từ từ Convs thành MSAs từ cuối baseline CNN lên
- Nếu MSAs vừa được thay không cải thiện performance, chuyển sang stage phía trước và thay Conv ở cuối stage bằng một MSA
- Sử dụng nhiều heads và nhiều dim hơn trong MSAs ở những stage cuối
Phụ lục
Inductive bias
Mình xin lỗi vì mình không biết dịch inductive bias như nào cho hay nên mình cứ để vậy nhé. Và bài viết này chủ yếu là về ViT và CNN nên mình sẽ không nói về Inductive bias của những dạng model khác như RNN.
Bạn nhớ khi thầy Yann LeCun sáng tạo ra CNN, hay lớp Convolution, thầy dựa trên giả định là những pixel ở gần nhau thì sẽ có liên quan đến nhau đây là Inductive bias đầu tiên của CNN, gọi là tính locality.
CNN còn một Inductive bias nữa, gọi là Weight Sharing: Các vùng trên ảnh sẽ được xử lý như nhau, đều được xử lý chung bởi một kernel, nhờ đó, CNN có thể nắm được đặc trưng vật dù vật đó có ở đâu trên ảnh đây là Inductive bias thứ 2 của CNN: weight sharing.
Hessian Eigenvalue
- Nếu ma trận Hessian dương (toàn bộ eigenvalue dương) tại điểm thì là một local minimum của
- Nếu ma trận Hessian âm (toàn bộ eigenvalue âm) tại điểm thì là một local maximum của
- Nếu ma trận Hessian là sự kết quả eigenvalue âm và dương, thì là điểm yên ngựa (saddle point) của
Trong Machine Learning, ta định nghĩa một hàm Loss và ta tìm điểm local minimum phù hợp (well global minimum là ngon nhất nhưng chắc là không tìm nổi đâu :v) để làm parameter cho model của chúng ta. Ta thường tối ưu hàm Loss sử dụng phương pháp tối ưu bậc một (Gradient Descent). Lúc này, eigenvalue của ma trận Hessian có ý nghĩa là: sự thay đổi độ dốc của hàm Loss khi chúng ta bước một khoảng cách vô cùng nhỏ theo một hướng nhất định.

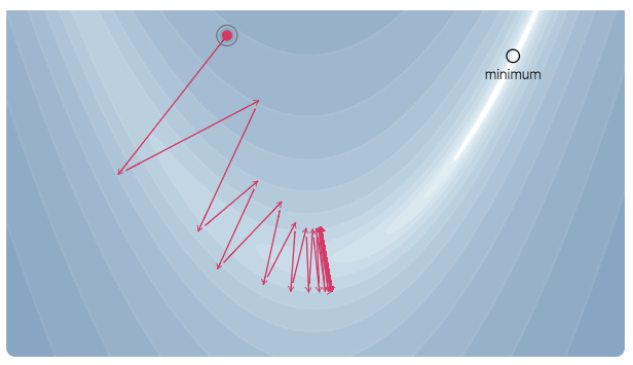
Khi Hessian eigenvalue dương và có giá trị lớn, thì nó sẽ là hình có dạng convex nhưng cực kì dốc. Lúc này, quá trình tối ưu sẽ gặp khá nhiều khó khăn do Gradient Descent sẽ nhảy đi nhảy lại trong vùng có độ dốc lớn và tiến rất chậm về điểm optima
Reference
Hessian Eigenvalue:
- https://www.quora.com/What-does-the-eigenvalue-of-a-Hessian-mean-in-machine-learning
- https://www.cs.toronto.edu/~rgrosse/courses/csc421_2019/slides/lec07.pdf
- https://web.stanford.edu/group/sisl/k12/optimization/MO-unit4-pdfs/4.10applicationsofhessians.pdf
How do Vision Transformers work?: https://arxiv.org/abs/2202.06709
All rights reserved
