Xác suất thống kê ứng dụng trong việc đổ công sức vào một mối quan hệ...
Bài đăng này đã không được cập nhật trong 5 năm
... hay hùng biện của một kẻ vã.
Foreword -- lời dạo đầu của tác giả.
Tác giả bài này hiện đang vừa viết vừa tìm hiểu thêm về chủ đề này nên có thể diễn đạt không được quá khoa học. Các trích dẫn có thể sẽ từ các trang tiếng Anh vì tác giả hơi mất gốc, tuy nhiên bài viết này tác giả sẽ viết nhiều tiếng mẹ đẻ nhất có thể.
Tại sao bài này liên quan đến machine learning?
Machine learning, sâu xa nhất, là tìm một distribution ngầm trong các hiện tượng tự nhiên cần được giải thích, từ distribution về khả năng trả nợ của một người dựa trên các yếu tố của người đó, cho đến distribution nhiều chiều về các tín hiệu (bao gồm cả ảnh, phim, tiếng, etc.) dựa trên các yếu tố ngầm định hướng các tính chất của tín hiệu đó. Vì vậy, việc bài này đưa ra giả thiết về một distribution ngầm và sự tồn tại về mối liên quan giữa thời gian và độ bền hoàn toàn nằm trong phạm trù của machine learning.
Abstract
Bài viết này xin được đưa ra giả thiết về mối liên quan giữa khoảng thời gian cò cưa nhau và độ bền của một mối quan hề, dựa trên các thông tin tạm coi là hiển nhiên. Nếu các bạn có thể và ủng hộ việc xây dựng một dataset với các thông tin liên quan, bài này có thể trở thành một nghiên cứu thực sự -- mình đoán thế.
Introduction and Motivation
Chắc hẳn có khá nhiều bạn đang ở trong tình trạng giống như mình: hiện tại mình đang tán một bạn Tinder, và bạn ấy nói rằng muốn từ từ vì muốn bền lâu. Mình ủng hộ ý kiến đó, tuy nhiên mình cũng hơi vã, nên muốn tìm hiểu một cách (có vẻ) khoa học xem bao lâu đến với nhau là đẹp. Về cơ bản là cần toán học chống lưng để mình còn gáy.
Ghi chú trước: theo như nhận xét người đọc, có chút dễ nhầm lẫn trong việc tính thời gian: thời gian cò cưa không tính vào thời gian độ dài của mối quan hệ. Nghĩa là, nếu hẹn hò 3 tháng và yêu nhau 1 năm thì tổng cộng họ đã vờn nhau được 5 mùa lận.
Existing works
Ngay lập tức trong đầu mình xuất hiện một bài toán xác suất mà mình đã đọc được từ xưa về việc chọn vợ/chồng thế nào để khả năng tìm được "nửa của mình" là cao nhất -- các bạn có thể đọc thêm ở trang wiki này. Nếu ngại đọc vì cái trang đó cũng vừa dài vừa nhiều ý quá thì để mình tóm tắt: nếu bạn tính rằng trong đời này bạn sẽ đi date tìm hiểu bạn khác giới lần, thì nếu bạn là con gái và đã date người, thì hãy cho mình số điện thoại ( ͡° ͜ʖ ͡°) Tuy nhiên, bài toán đó, cho dù quan trọng và hơn hết là optimal, không thực sự áp dụng vào trường hợp mình đang gặp phải.
Model specification
Dựa theo law of large numbers, mình sẽ đặt một giả thiết khá hợp lý là khả năng (xác suất) của độ bền của một mối quan hệ (tính theo năm) dựa trên thời gian cò cưa nhau (tính theo năm) là một parameterized Gaussian distribution. Cụ thể hơn, cái parameter đó là thời gian cò cưa, event của distribution đó là độ dài của mối quan hệ, và giá trị xác suất là về khả năng độ dài mối quan hệ đó sẽ xảy ra.
Cụ thể, nếu đặt thời gian tán nhau là , thì xác suất của độ dài của mối quan hệ sẽ là
với và là các hàm theo thời gian trồng cây si. Để đơn giản hoá vấn đề mà không mất tính tổng quát, nếu độ dài của mối quan hệ là âm nghĩa là mối quan hệ đó còn không thể bắt đầu.
Sau đây là các "sự thật khá hiển nhiên" được sử dụng làm giả thiết:
- Thời gian ở với nhau càng lâu thì tình cảm càng bền -- đây cũng thuộc về khái niệm "hết tình còn nghĩa," tuy nhiên bài này không liên quan đến tâm lý học nên sự thật này chỉ mang ý nghĩa rằng hàm tỉ lệ thuận.
- Có thể giả thiết rằng hàm dốc hơn tuyến tính, và tương tự hàm thoải hơn tuyến tính: một mối quan hệ đến càng nhanh tan càng chóng vánh (quen nhau một ngày đá nhau một tuần), và mối qua hệ nén càng lâu thì sẽ tồn tại càng dài (quen nhau 5 năm yêu nhau cả đời).
- Độ dài của một mối quan hệ không thể chắc chắn tính được bằng khoảng thời gian cò cưa nhau, vì trên đời này chả có gì chắc kèo như vậy cả. Bạn có thể gặp may mắn tìm được nửa còn lại và nhận ra ngay lập tức như Lily và Marshall (hơi viễn tưởng), hoặc bạn có thể hẹn hò với Hari Won 10 năm rồi chỉ để nhìn em ấy ra đi và cưới một người khác... (đen.)
- Dựa trên thông tin cá nhân (và các bạn khác), hiện đây là một số data biểu mẫu để chọn hàm:
| 1/365 (1 ngày) | 4/365 (4 ngày) |
| 1/52 (1 tuần) | 1/4 (3 tháng) |
| 0.5 | 0.75 |
| 1 | 0.9 |
| 1 | 2 |
| 2 | 5 |
| 5 | 60 |
và plot ra để ta tạm chọn hàm: . Chúng ta có thể xài MLP (multilayer perceptron) hoặc SVM (support vector machine) hoặc dăm ba các thuật toán "học máy" khác để chọn, nhưng vì đang tạo giả thiết nên mình chỉ chọn hàm đơn giản vậy thôi.
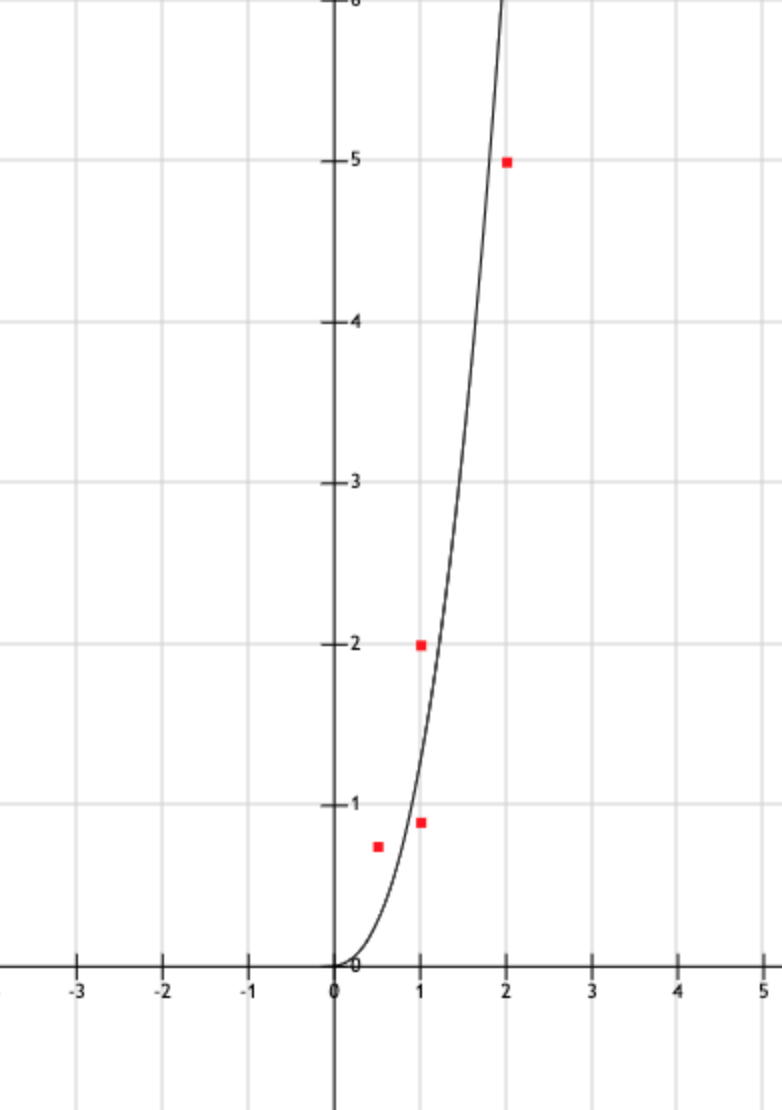
Dựa trên hàm đó, chúng ta sẽ tính được khoảng cách giữa data thật và trung bình của data đó để ước lượng 1 sigma:
| 1/365 | ||
| 1/52 | ||
| 0.5 | 0.279 | 0.471 |
| 1 | 1.269 | 0.369 |
| 1 | 1.269 | 0.731 |
| 2 | 6.391 | 1.391 |
| 5 | 58.739 | 1.261 |
Tương tự chúng ta plot ra:
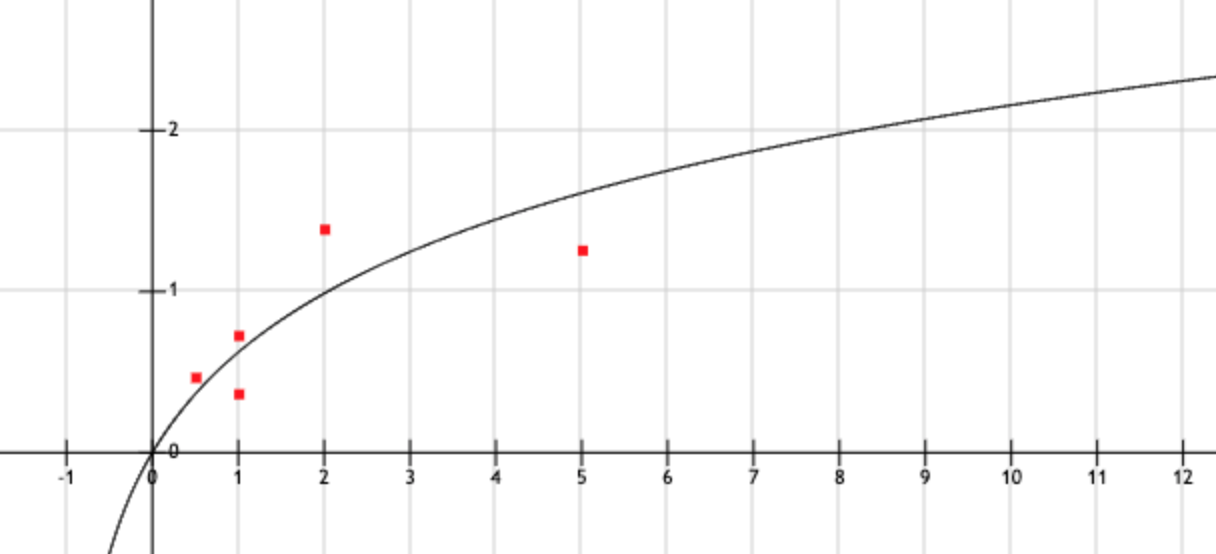
và chọn .
Lưu ý, khi chọn các hàm này cần để ý xem liệu hàm đó có tồn tại (được định nghĩa) ở tất cả các điểm ; đó là lý do tại sao có những hàm log khác khớp hơn nhiều nhưng không được chọn. Đồng thời, theo Occam's Razor, khi bạn chọn một model cho một vấn đề, hãy chọn nó đơn giản nhất có thể, vì nó sẽ giúp bạn generalize được kết quả đó ra những data point không tồn tại trong training set.
Results
Để thuyết phục được bạn gái rằng từng này thời gian là đủ cho tương lai (lol), có sẵn độ dài mối quan hệ muốn có và hướng tới xác suất , chúng ta cần tìm sao cho
với là CDF của distribution đó. Để không quá lằng nhằng với công thức toán học, mình xin được giới thiệu một tail bound (lower bound for tail integral) cho normal distribution -- các bạn có thể đọc thêm tại đây nếu tò mò:
Công thức trên là dành cho standard normal distribution nên chúng ta phải mổ xẻ nó chút: định nghĩa của vế trái đó là -- ghi chú, công thức sau được trích dẫn thẳng từ nguồn nên hơi lẫn, chỉ trong công thức tiếp theo ám chỉ một biến số chung chung chứ không liên quan cụ thể đến bài toán hiện tại:
Trong trường hợp này, thay thế các số chúng ta cần -- tạm tính nếu chỉ cần mối quan hệ dài một năm (tớ xin lỗi  ), chúng ta cần có
), chúng ta cần có
và
Thay thế công thức cho mean và standard deviation ta có
Khảo sát hàm cho phương trình tail bound, ta có thấy nó đặt giá trị tối đa
tại
Thay giá trị vừa tìm được ở trên vào công thức với , ta có
nghĩa là, với xác suất gần 40%, mối quan hệ của bạn sẽ dài 1 năm trở lên nếu bạn tán nó hơn 9 tháng mới đổ.
thế này thì lỗ nặng rồi.
Analysis & Future work
Với một dataset, chúng ta có thể đoán (extrapolate) được distribution của và dựa vào các thuật toán học máy. Việc đó theo lý thuyết sẽ tăng độ chính xác của mô hình này, tuy nhiên sẽ khó có được một công thức cụ thể (closed form) cho bài toán này nữa, và việc tìm nghiệm cho 2 công thức trên kia đã đủ khó rồi. Với model căng hơn, khả năng chúng ta sẽ phải xài một optimizer để tìm các cực trị để giải bài toán trên.
Một việc nữa là tail bound này chưa được chặt nên chỉ có thể đảm bảo một khả năng chưa được to lắm. 40% là khả năng lớn nhất mà model trên có thể đảm bảo, và với nhiều cặp đôi có thể đó là chưa đủ. Để tăng tính chuẩn xác, chúng ta có thể thay cái tail bound đó bằng công thức tích phân cụ thể, nhưng điều đó sẽ làm cho công thức còn rối hơn nữa: không có closed form đạo hàm để xài Gradient Descent/Ascent luôn, mà phải dùng những thuật toán như bisection method hay gì đó. Tuy nhiên, với một xác suất thấp như vậy mà để yêu nhau được một năm phải mất tận 9 tháng tán tỉnh thì không hợp với môi trường trên Tinder lắm; nhưng kết quả này có thể đáng cho những cặp đôi muốn hướng tới sự bền vững.
Hoặc chỉ đơn giản là tán thành công bạn đó để khỏi phải nghĩ những bài toán như thế này nữa 
All rights reserved
