Trong bài viết, mình sẽ giới thiệu một trong những thuật toán cơ bản nhất của Machine Learning. Học có giám sát (Supervised Learning) được chia ra làm 2 dạng lớn là hồi quy (regression) và phân loại (classification) dựa trên tập dữ liệu mẫu - tập huấn luyện (training data). Với bài đầu tiên này ta sẽ bắt đầu bằng bài toán hồi quy mà cụ thể là hồi quy tuyến tính (linear regression).

1. Định nghĩa

Mục tiêu của giải thuật hồi quy tuyến tính là dự đoán giá trị của một hoặc nhiều biến mục tiêu liên tục (continuous target variable) y dựa trên một vector đầu vào x.

Ví dụ: dự đoán giá nhà ở Hà Nội dựa vào thông tin về diện tích, vị trí, năm xây dựng của ngôi nhà thì tt ở đây sẽ là giá nhà và 1. Định nghĩa Mục tiêu của giải thuật hồi quy tuyến tính là dự đoán giá trị của một hoặc nhiều biến mục tiêu liên tục (continuous target variable) y dựa trên một vector đầu vào x.

Ví dụ: dự đoán giá nhà ở Hà Nội dựa vào thông tin về diện tích, vị trí, năm xây dựng của ngôi nhà thì t ở đây sẽ là giá nhà và 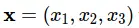với x1 là diện tích, x2 là vị trí và x3 là năm xây dựng.

Nếu bạn còn nhớ thì đây chính là phương pháp phân tích hồi quy của xác suất thống kê. Mọi lý thuyết cơ bản của phương pháp này vẫn được giữa nguyên nhưng khi áp dụng cho máy tính thì về mặt cài đặt có thay đổi đôi chút.

Về cơ bản thì ta sẽ có một tập huấn luyện chứa các cặp 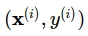tương ứng và nhiệm vụ của ta là phải tìm giá trị 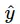ứng với một đầu vào x mới. Để làm điều này ta cần tìm được quan hệ giữa x và y để từ đó đưa ra được dự đoán. Hay nói cách trừu tượng hơn là ta cần vẽ được một đường quan hệ thể hiện mối quan hệ trong tập dữ liệu.

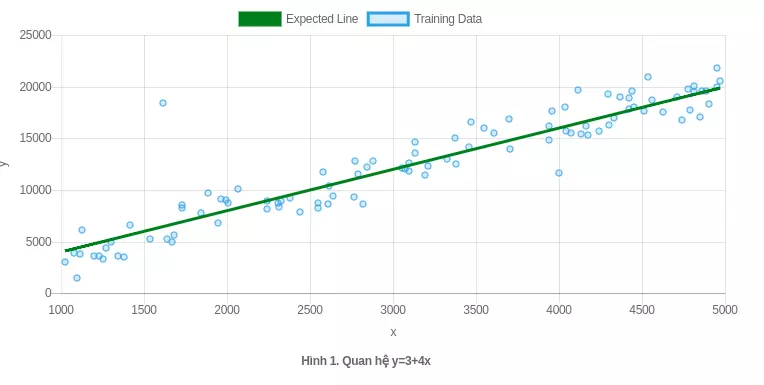
Như hình minh họa phía trên thì ta có thể vẽ được một đường màu xanh y=3+4x để thể hiện quan hệ giữa x và y dựa vào các điểm dữ liệu huấn luyện đã biết. Thuật toán hồi quy tuyến tính sẽ giúp ta tự động tìm được đường màu xanh đó để từ đó ta có thể dự đoán được y cho một x chưa từng xuất hiện bao giờ.

2. Mô hình

Mô hình đơn giản nhất là mô hình kết hợp tuyến tính của các biến đầu vào:

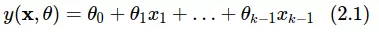trong đó

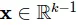: là vector biến đầu vào

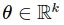: là vector trọng số tương ứng.

Thường θ được gọi là tham số của mô hình. Giá trị của tham số sẽ được ước lượng bằng cách sử dụng các cặp giá trị 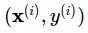của tập huấn luyện. Thực ra mô hình tuyến tính là chỉ cần ở mức tuyến tính giữa tham số θ và y là đủ. Và mình cho rằng tên gọi tuyến tính là xuất phát giữa θ và y, chứ không phải giữa x và y. Nói cách khác, ta có thể kết hợp các x một cách phi tuyến trước khi hợp với θ để được y. Một cách đơn giản là sử dụng hàm phi tuyến cho x như sau:

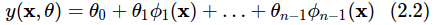
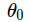được gọi là độ lệch (bias) nhằm cắt đi mức độ chênh lệch giữa mô hình và thực tế. Các hàm phi tuyến 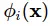này được gọi là các hàm cơ bản (basic function). Thường người ta sẽ đặt 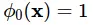và viết lại công thức trên như sau:

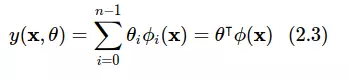Như quy ước thì tất cả các vector nếu không nói gì thì ta ngầm định với nhau rằng nó là vector cột nên ta có được cách viết nhân ma trận như trên.

3. Chọn hàm cơ bản

Việc chọn hàm cơ bản ϕ(x) cũng chính là chọn tính năng cho đầu vào rất quan trọng trong học máy. Ngoài ra việc chọn ra sao còn ảnh hưởng tới tốc độ và bộ nhớ để tính toán nữa. Ở đây tôi chỉ để cập tới 1 vài cách đơn giản để chọn hàm cơ bản mà thôi.

3.1. Giữ nguyên đầu vào

Giữ nguyên đầu vào có ý là không thay đổi giá trị đầu vào, tức: ϕ(x)=x Thường người ta sẽ gom các đầu vào thành một ma trận 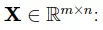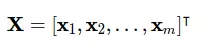Mỗi hàng của ma trận chứa 1 mẫu và mỗi cột sẽ chứa các thuộc tính đầu vào.

3.2. Chuẩn hoá đầu vào

Là phương pháp co giãn các thuộc tính về khoảng [min,max] nào đó (thường là [−1,1] hoặc [−0.5,0.5]) dựa vào kì vọng và độ lệch chuẩn của chúng. 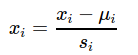Trong đó, 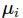là trung bình, còn 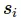là độ lệch chuẩn của tính năng i. Đôi lúc người ta cũng có thể lấy 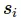là khoảng rộng chuẩn 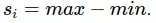Việc này không làm mất tính chất phân phối của chúng nên không ảnh hưởng tới kết quả học. Nhưng lại giúp cho việc học trở lên dễ dàng hơn vì các thuộc tính gần như cùng khoảng nhỏ với nhau. Phương pháp này còn có tên khác là chuẩn hoá trung bình (mean normalization).

3.3. Đa thức hoá

Sử dụng đa thức bậc cao để làm đầu vào: 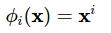Với các bài toán hồi quy tuyến tính thì phương pháp này rất hay được sử dụng.

3.4. Sử dụng hàm Gaussian

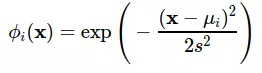
ở đây: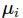sẽ chỉ định vị trí trung bình cho đầu vào còn s sẽ chỉ định độ phân tán cho đầu vào. Việc sử dụng hàm này sẽ giúp ta có được đầu vào theo phân phối chuẩn.

3.5. Sử dụng hàm sigmoid

Tương tự như hàm Gaussian, ta có thể sử dụng hàm sigmoid để biến đổi đầu vào: 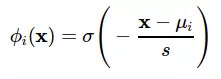Hàm sigmoid được sử dụng là sigmoid chuẩn:

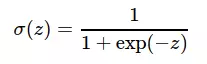Một biến thể khác là sử dụng tanhtanh vì nó khá gần với sigmoidsigmoid:

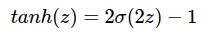
Ở phần sau chúng ta sẽ tiếp tục tìm hiểu về cách ước lượng tham số trong hàm lỗi, để đánh giá mức độ chênh lệch và thực hành 1 số ví dụ về Hồi quy tuyến tính.