Dark Knight @trungson077

1.3K 60 12

Đã đăng vào thg 5 18, 2020 9:49 SA

trong

15 phút đọc

2.6K

Quantum Machine Learning - Khi Vật Lý Lượng Tử Và Machine Learning Gặp Nhau

Bài đăng này đã không được cập nhật trong 3 năm

Các tính chất cơ bản của Quantum Mechanic

Quantum mechanics (QM; also known as quantum physics, quantum theory, the wave mechanical model and matrix mechanics), including quantum field theory, is a fundamental theory in physics describing the properties of nature on an atomic scale.

Dịch nghĩa: Cơ học lượng tử, bao gồm cả lý thuyết trường lượng tử là một nền tảng của vật lý nhằm miêu tả các thuộc tính(tính chất) của tự nhiên ở mức độ nguyên tử.

Các nguyên lý của cơ học cổ điển áp dụng cho thế giới vĩ mô đã không còn phản ánh chính xác hoạt động ở mức vi mô của các hạt nguyên tử và hạ nguyên tử. Cơ học lượng tử cho rằng năng lượng (energy — thứ căn bản cấu thành vũ trụ) là một dạng vật chất nên có thể đong, đo, định lượng và chia thành các đơn vị.

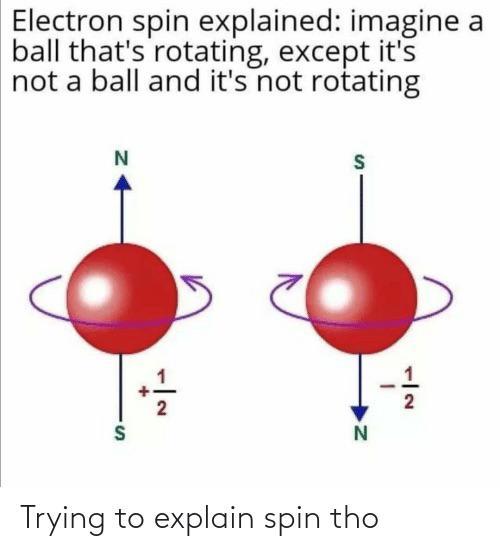
Spin

Những vật lớn như một hành tinh hoặc nhỏ như một proton đều có một tính chất gọi là spin.

Spin là lượng chuyển động quay mà một vật có, xét cả khối lượng và hình dạng của nó. Đây còn được gọi là moment động lượng của một vật. Spin là một khái niệm thuần túy lượng tử, không có sự tương ứng trong cơ học cổ điển.

Quan niệm về spin sau đó được chứng tỏ rằng có mâu thuẫn với thuyết tương đối. Tuy nhiên, cho dù nguồn gốc sinh ra spin như thế nào chưa rõ, spin của tất cả các hạt cơ bản tạo nên thế giới vật chất, như electron, quark đều khác không và bằng ħ/2 (ħ là hằng số plank), gọi tắt là 1/2. Các hạt như photon có spin bằng 1… Như vậy, spin là một đặc trưng nội tại của hạt, nó cố hữu giống như khối lượng và điện tích đặc trưng của hạt đó. Nếu một electron không có spin thì nó không còn là một electron nữa.

Chồng chập lượng tử và Qubit

Chồng chập lượng tử (hay chồng chất lượng tử, xếp lớp lượng tử) là việc áp dụng nguyên lý chồng chập vào cơ học lượng tử. Nguyên lý chồng chập vốn là sự cộng véctơ các véctơ sóng trong giao thoa. Trong cơ học lượng tử, các véctơ hàm sóng, hay véctơ trạng thái được cộng.

Cụ thể, chồng chập lượng tử có thể được phát biểu là “nếu một hệ lượng tử có thể được phát hiện ở một trong 2 trạng thái, A và B với các tính chất khác nhau, nó cũng có thể được phát hiện ở trạng thái tổ hợp của chúng, aA + bB, ở đó a và b là các số bất kỳ”.

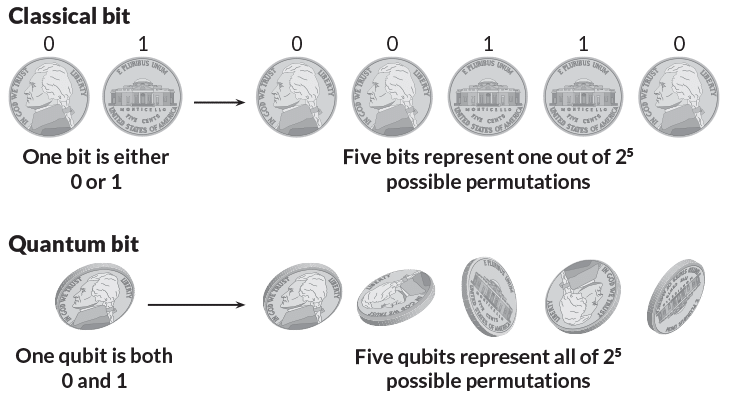
Điều này được ứng dụng vào máy tính lượng tử với việc tạo ra các quantum bit (bit lượng tử), gọi tắt là qubit. Các nhà phát minh máy tính lượng tử sử dụng một vi hạt như một qubit, và trạng thái spin hướng lên hay hướng xuống của vi hạt tương ứng với trạng thái của qubit.

Khác với máy tính kỹ thuật số dựa trên tranzitor đòi hỏi cần phải mã hóa dữ liệu thành các chữ số nhị phân, mỗi số được gán cho 1 trong 2 trạng thái nhất định là 0 hoặc 1, tính toán lượng tử sử dụng các bit lượng tử ở trong trạng thái chồng chập để tính toán. Điều này có nghĩa là 1 bit lượng tử có thể có giá trị 0 và 1 ở cùng 1 thời điểm, tức là xảy ra hiện tường chồng chập lượng tử của qubit.

Để giải thích điều này, hãy hình dung rằng có một đồng tiền được tung lên. Trước khi nó tiếp đất bằng mặt trước hay mặt sau, nó sẽ quay tít trong không trung với tốc độ cực nhanh. Và khi nó đang quay tít như vậy, tại một thời điểm nhất định bạn xác định mặt của đồng xu thì nó sẽ có cả 2 trạng thái, sấp và ngửa.

Như vậy, nếu một máy tính có 2 qubit, tại một thời điểm nó sẽ có $2^2$ = 4 trạng thái, 3 qubit sẽ có $2^3$ = 8 trạng thái, $N$ qubit sẽ có $2^N$ trạng thái của qubit đồng thời. Điều này có nghĩa là chiếc máy tính lượng tử $N$ qubit sẽ có tương đương với sức mạnh của $2^N$ máy tính chạy song song nhau. Điều này lý giải tại sao máy tính lượng tử có khả năng tính toán cực nhanh so với máy tính thông thường.

Về mặt lý thuyết, một máy tính có nhiều qubit có khả năng xử lý một lượng tác vụ vô cùng lớn như tính toán số học hoặc thực hiện tìm kiếm cơ sở dữ liệu cực lớn trong thời gian nhanh hơn nhiều so với các máy tính thông thường.

Rối lượng tử (Quantum Entanglement)

Rối lượng tử (Quantum Entanglement) là một hiện tượng xảy ra ở cấp độ hạt mà tới nay các nhà khoa học vẫn chưa giải thích được. Đó là việc sánh đôi và tương tác lẫn nhau ở hai hạt trong vũ trụ hoàn toàn không phụ thuộc vào khoảng cách giữa chúng. Nghĩa là nếu như bạn có một hạt photon ở đầu này của vũ trụ và một hạt photon khác có liên kết rối lượng tử với nó, nhưng ở tận đầu kia của vũ trụ, thì nếu bạn tác động vào một hạt, hạt kia cũng sẽ bị ảnh hưởng. Tương tác này nhanh hơn ánh sáng rất nhiều và hoàn toàn tuyệt đối. Hay nói cách khác: NÓ KHÔNG PHỤ THUỘC VÀO KHOẢNG CÁCH GIỮA HAI HẠT.

Sự khác biệt của qubit so với bit cổ điển, không chỉ ở sự biến thiên giá trị liên tục thông qua chồng chập lượng tử, mà còn ở chỗ cùng một lúc nhiều qubit có thể tồn tại và liên hệ với nhau qua hiện tượng rối lượng tử . Sự vướng víu này có thể xảy ra ở khoảng cách vĩ mô giữa các qubit, cho phép chúng thể hiện các chồng chập cùng lúc của nhiều dãy ký tự (ví dụ chồng chập 01010 và 11111). Tính chất “song song lượng tử” này là thế mạnh cơ bản của máy tính lượng tử.

Quantum machine learning

Hiểu về khái niệm tính toán lượng tử trong 1 phút

Bây giờ bạn có thể tự hỏi: "Quantum algorithm là gì?". Nó cũng chỉ đơn giản là một chuỗi các lệnh như mọi thuật toán thông thường. Ở những máy tính thông thường chúng ta sử dụng classic gates như OR, AND, NOT. Nhưng điều làm cho tính toán lượng tử khác với các phép toán thông thường là nó sử dụng quantum gates, hoạt động trên qubits thay vì bit. Vậy input của quantum algorithms được tạo lên từ qubits, đơn giản như nếu như bạn có n qubits thì đồng thời bạn cũng có $2^n$ trạng thái, với 300 qubits thì bạn có $2^{300}$ trạng thái xảy ra cùng lúc, $2^{300}$ cũng chính là số nguyên tử trong toàn bộ vũ trụ ^^

Một ví dụ điển hình ở ngoài đời sống mà áp dụng về tính toán lượng tử là Bộ xử lý siêu dẫn của google sử dụng 54 qubits để thực hiện phép toán mất 200s mà máy tính thông thường với các thuật toán hiện có thời nay cần đến 10,000 năm để giải ra.

Quantum machine learning là gì?

Quantum machine learning là một nghành nghiên cứu mới kết hợp giữa quantum physics và machine learning. Với mục tiêu phát triển các thuật toán lượng tử học từ dữ liệu để cải thiện các phương pháp hiện có trong học máy.

QML đã có những phát kiến rực rỡ về mặt toán học, khi mà toán học là nền tảng cốt lõi cho các thuật toán lượng tử. Nhưng thực tế các phát kiến này vẫn chưa được khai thác nhiều và các thuật toán ML thông thường dùng trong Artificial Neural Networks (ANNs) vẫn tỏ ra hữu dụng khi chạy trên các máy tính truyền thống. Nhưng theo xu thế mới của thời đại 4.0 khi Big Data là chủ đạo và yêu cầu xử lý nghiệp vụ ngày càng cao của các doanh nghiệp, QML sẽ dần thay thế ML truyền thống. Thêm vào đó, các chuyên ngành như Quantum Computer Science và Quantum Information Science sẽ tạo ra những thay đổi lớn lao cho AI trong vòng 10 năm tới và là tiền đề cho kỷ nguyên công nghiệp mới 5.0.

Vậy QML sẽ thay thế và hỗ trợ cho ML truyền thống như thế nào? Có 2 hướng chính:

Quantum versions of ML algorithms: (1) sử dụng các phiên bản lượng tử trong việc tìm trị riêng và vector riêng của các ma trận lớn, (2) tìm kiếm nearest neighbours trong máy tính lượng tử, (3) các phương pháp lượng tử trong việc cải tiến thí nghiệm trên các hạt Higgs boston tạo nên khuôn khổ về sự hiểu biết các hạt và tương tác cơ bản trong tự nhiên, hay (4) các thuật toán lượng tử để giải quyết các bài toán tuyến tính trong ML.
Classical ML to analyze quantum systems: (1) nhận diện các điểm thay đổi lượng tử (Quantum Change Point), (2) phân loại nhị phân về trạng thái của các qubit, (3) sự mất liên kết lượng tử, và (4) tái tạo các giá trị quan sát trong nhiệt động học.

Quantum neural network

Quantum neural network(QNN) là mô hình mạng neural dưa trên các nguyên tắc cơ bản của vật lý lượng tử như qubit, superposition... và chỉ sử dụng $O(\log(N))$ tham số biến thiên cho đầu vào là $N$ qubits.

Thực thi QNNs là một trong những bước tiến quan trọng trong AI và ML. Những bước đầu tiên là mô phỏng Perception trong QNNs hay nói khác đi là mô phỏng một neutron lượng tử. Chúng ta có thể dựa vào thuyết diễn giải nhiều thế giới — Many-worlds Interpretation để mô phỏng cho neutron. Thuyết diễn giải nhiều thế giới cho rằng tồn tại song song nhiều vũ trụ quanh chúng ta với quá khứ và tương lai hoàn toàn xác định. Vậy học thuyết này có liên quan gì tới QNNs? Có thể hiểu đơn giản là ANNs sử dụng một mạng neural để lưu giữ các patterns khác nhau nhưng QNNs có thể sử dụng cùng một lúc nhiều mạng neural để lưu trữ nhiều patterns khác nhau. Nghe có vẻ khá trừu tượng nhỉ? Các bạn có thể hình dung nó như qubit tồn tại 2 trạng thái là 0 và 1 ở cùng 1 thời điểm (Superposition).

Hybrid quantum-classical

Xuyên suốt bài bạn đã năm được các khái niệm cơ bản rồi chứ , bây giờ chúng ta sẽ sử dụng TensorFlow Quantum để xây dựng một mạng lượng tử lai, ta sẽ dùng mạng neural net để kiểm soát một qubit duy nhất. Sự kiểm soát sẽ được tối ưu hóa để chuẩn bị chính xác qubit ở trạng thái 0 hoặc 1, cụ thể hơn nó sẽ học để kiểm soát lỗi của một hệ thống ta sẽ mô phỏng dưới đây:

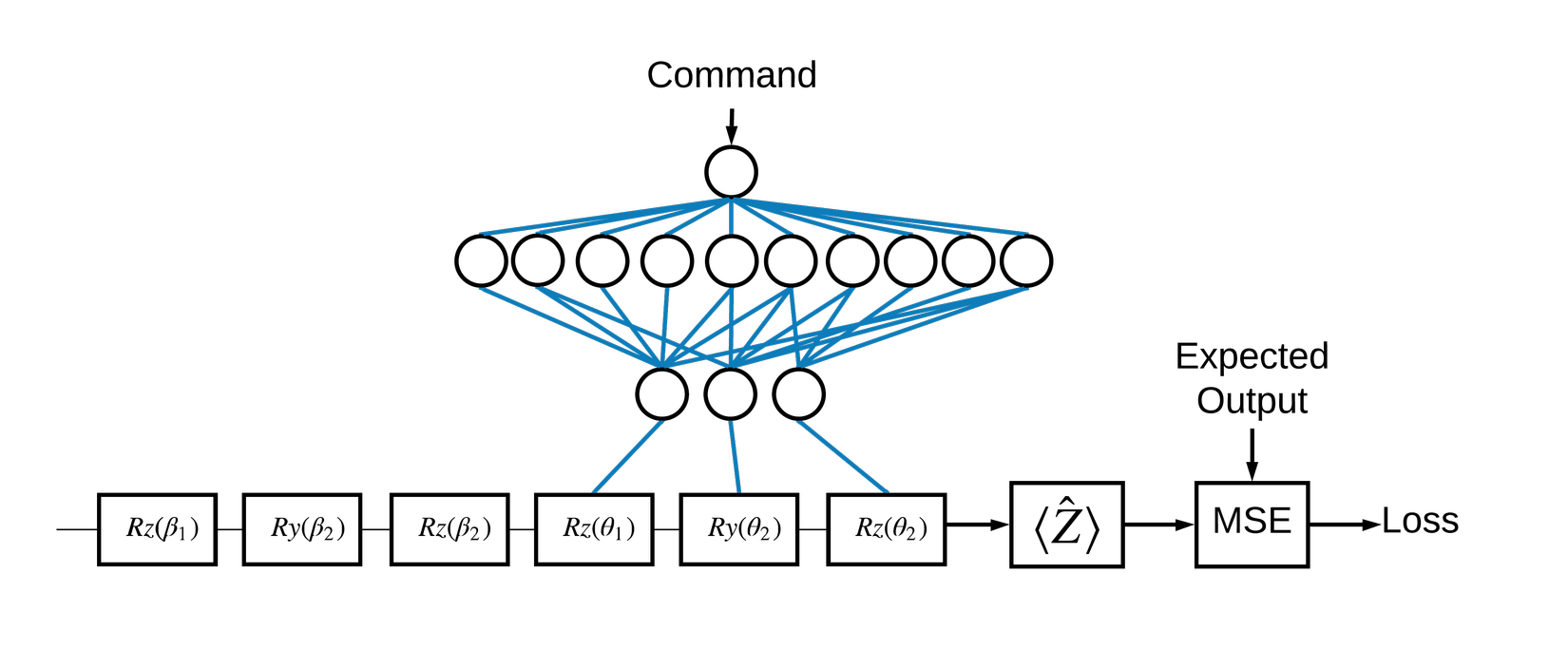
Đầu tiền ta sẽ khởi tạo một vòng bit trong một Controller Circuit

# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')

# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
    cirq.rz(control_params[0])(qubit),
    cirq.ry(control_params[1])(qubit),
    cirq.rx(control_params[2])(qubit))

SVGCircuit(model_circuit)

Xây dựng bố cục mạng đơn giản bằng keras (controller network):

controller = tf.keras.Sequential([
    tf.keras.layers.Dense(10, activation='elu'),
    tf.keras.layers.Dense(3)
])

Sử dụng tfq để kết nối với controller circuit như một keras.Model:

# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
                                # The circuit-tensor has dtype `tf.string` 
                                dtype=tf.string,
                                name='circuits_input')

# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
                                dtype=tf.dtypes.float32,
                                name='commands_input')

Tiếp theo áp dụng một loạt các phép tính cho các đầu vào đó, để tính toán:

dense_2 = controller(commands_input)

# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
                                             # Observe Z
                                             operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])

Bây giờ đóng gói tính toán này bằng bằng một tf.keras.Model:

# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
                       outputs=expectation)

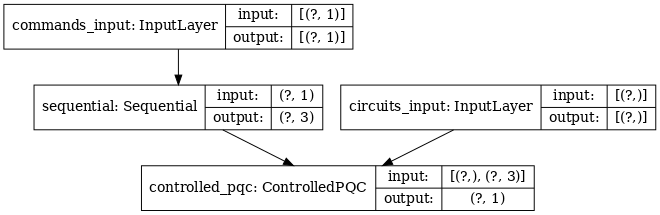
Draw model:

Mô hình này có hai đầu vào: Các lệnh cho bộ điều khiển và đầu ra của controller circuit

tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)

Xây dựng command input values đầu vào và đầu ra mong muốn:

Đây không phải là toàn bộ dữ liệu đào tạo cho nhiệm vụ này. Mỗi datapoint trong tập dữ liệu cũng cần một mạch đầu vào, ta sẽ nói rõ hơn điều này ở đoạn kế tiếp

commands = np.array([[0], [1]], dtype=np.float32)
expected_outputs = np.array([[1], [-1]], dtype=np.float32)

Input-circuit bên dưới xác định tính toán sai ngẫu nhiên mà mô hình sẽ học để sửa:

random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
  cirq.rx(random_rotations[0])(qubit),
  cirq.ry(random_rotations[1])(qubit),
  cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
  noisy_preparation
] * 2)  # Make two copied of this circuit

datapoint_circuits.shape

Output:

TensorShape([2])

Tiếp tục chúng ta sẽ xây dựng các hàm cho quá trình training:

optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
                    y=expected_outputs,
                    epochs=30,
                    verbose=0)

plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()

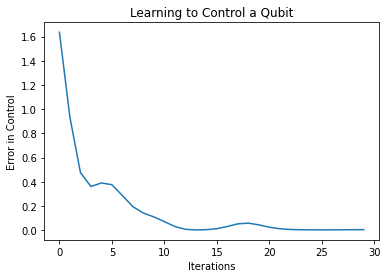
Từ plot trên bạn có thể thấy quá trình mạng đã học cách khắc phục tính toán sai của hệ thống.

Chúng ta vừa đi qua một loạt các khái niệm cơ bản về quantum machine learning, cũng như bàn luận về nó. Mặc đây là một công nghệ khá non trẻ nhưng tiềm năng của nó lại rất lớn trong trí tuệ nhân tạo, cảm ơn các bạn đã đọc bài, hẹn các bạn trong bài viết tiếp theo