Mạng nơ-ron nhân tạo (Neural Network - NN) là một mô hình lập trình rất đẹp lấy cảm hứng từ mạng nơ-ron thần kinh. Kết hợp với các kĩ thuật học sâu (Deep Learning - DL), NN đang trở thành một công cụ rất mạnh mẽ mang lại hiệu quả tốt nhất cho nhiều bài toán khó như nhận dạng ảnh, giọng nói hay xử lý ngôn ngữ tự nhiên.

Trong bài này, ta sẽ cùng tìm hiểu và cài đặt một NN cơ bản để làm nền tảng cho các bài về học sâu tiếp theo.

1. Perceptrons

1.1. Perceptron cơ bản

Một mạng nơ-ron được cấu thành bởi các nơ-ron đơn lẻ được gọi là các perceptron. Nên trước tiên ta tìm hiểu xem perceptron là gì đã rồi tiến tới mô hình của mạng nơ-ron sau. Nơ-ron nhân tạo được lấy cảm hứng từ nơ-ron sinh học như hình mô tả bên dưới:

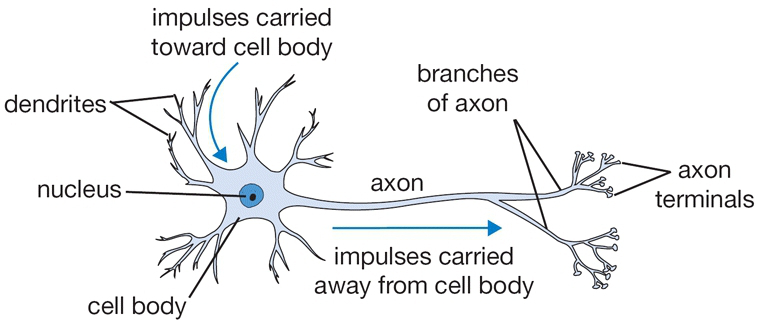
Như hình trên, ta có thể thấy một nơ-ron có thể nhận nhiều đầu vào và cho ra một kết quả duy nhất. Mô hình của perceptron cũng tương tự như vậy:

Một perceptron sẽ nhận một hoặc nhiều đầu \mathbf{x}x vào dạng nhị phân và cho ra một kết quả oo dạng nhị phân duy nhất. Các đầu vào được điều phối tầm ảnh hưởng bởi các tham số trọng lượng tương ứng \mathbf{w}w của nó, còn kết quả đầu ra được quyết định dựa vào một ngưỡng quyết định bb nào đó:

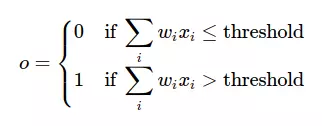
Đặt b=−threshold, ta có thể viết lại thành:

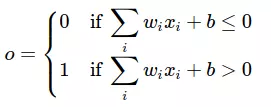
Để dễ hình dung, ta lấy ví dụ việc đi nhậu hay không phụ thuộc vào 4 yếu tố sau:

• 1. Trời có nắng hay không?
• 2. Có hẹn trước hay không?
• 3. Vợ có vui hay không?
• 4. Bạn nhậu có ít khi gặp được hay không? Thì ta coi 4 yếu tố đầu vào là x_1, x_2, x_3, x_4 và nếu o=0 thì ta không đi nhậu còn o=1 thì ta đi nhậu. Giả sử mức độ quan trọng của 4 yếu tố trên lần lượt là w_1=0.05, w_2=0.5, w_3=0.2, w_4=0.25w và chọn ngưỡng b=−0.5 thì ta có thể thấy rằng việc trời nắng có ảnh hưởng chỉ 5% tới quyết định đi nhậu và việc có hẹn từ trước ảnh hưởng tới 50% quyết định đi nhậu của ta. Nếu gắn x_0=1và w_0=b, ta còn có thể viết gọn lại thành:

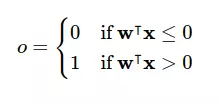
1.2. Sigmoid Neurons

Với đầu vào và đầu ra dạng nhị phân, ta rất khó có thể điều chỉnh một lượng nhỏ đầu vào để đầu ra thay đổi chút ít, nên để linh động, ta có thể mở rộng chúng ra cả khoảng [0, 1]. Lúc này đầu ra được quyết định bởi một hàm sigmoid σ(w^⊺ x). Như các bài trước đã đề cập thì hàm sigmoid có công thức:

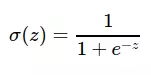
Đồ thị của hàm này cũng cân xứng rất đẹp thể hiện được mức độ công bằng của các tham số:

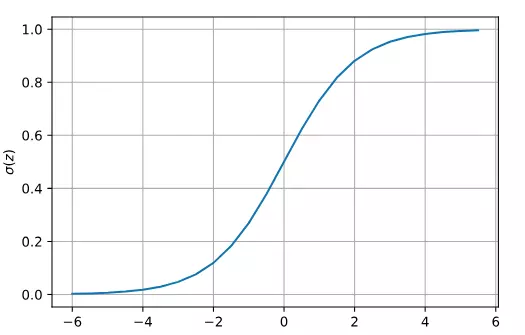
Đặt z = w ⊺x thì công thức của perceptron lúc này sẽ có dạng:

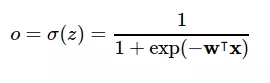
Tới đây thì ta có thể thấy rằng mỗi sigmoid neuron cũng tương tự như một bộ phân loại tuyến tính (logistic regression) bởi xác suất P(y_i=1∣x_i ;w) = σ(w^⊺ x). Thực ra thì ngoài hàm sigmoid ra, ta còn có thể một số hàm khác như tanh ReLU để thay thế hàm sigmoid bởi dạng đồ thị của nó cũng tương tự như sigmoid. Một cách tổng quát, hàm perceptron được biểu diễn qua một hàm kích hoạt (activation function) f(z) như sau: o = f(z) = f(w^⊺ x) Bằng cách biểu diễn như vậy, ta có thể coi neuron sinh học được thể hiện như sau:

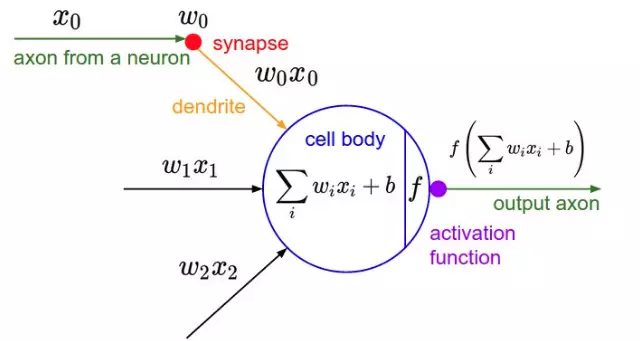
Một điểm cần lưu ý là các hàm kích hoạt buộc phải là hàm phi tuyến. Vì nếu nó là tuyến tính thì khi kết hợp với phép toán tuyến tính w^⊺ x thì kết quả thu được cũng sẽ là một thao tác tuyến tính dẫn tới chuyện nó trở nên vô nghĩa.

2. Kiến trúc mạng NN

Mạng NN là sự kết hợp của của các tầng perceptron hay còn được gọi là perceptron đa tầng (multilayer perceptron) như hình vẽ bên dưới:

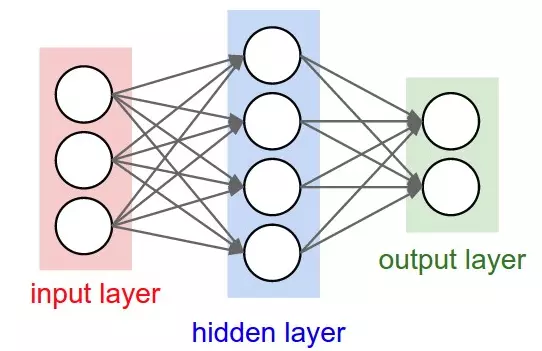
Một mạng NN sẽ có 3 kiểu tầng:

• Tầng vào (input layer): Là tầng bên trái cùng của mạng thể hiện cho các đầu vào của mạng.
• Tầng ra (output layer): Là tầng bên phải cùng của mạng thể hiện cho các đầu ra của mạng.
• Tầng ẩn (hidden layer): Là tầng nằm giữa tầng vào và tầng ra thể hiện cho việc suy luận logic của mạng. Lưu ý rằng, một NN chỉ có 1 tầng vào và 1 tầng ra nhưng có thể có nhiều tầng ẩn.

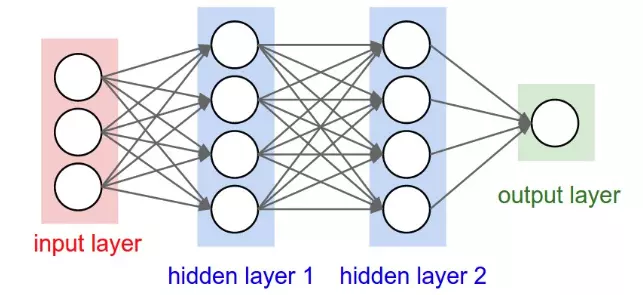
Trong mạng NN, mỗi nút mạng là một sigmoid nơ-ron nhưng hàm kích hoạt của chúng có thể khác nhau. Tuy nhiên trong thực tế người ta thường để chúng cùng dạng với nhau để tính toán cho thuận lợi.

Ở mỗi tầng, số lượng các nút mạng (nơ-ron) có thể khác nhau tuỳ thuộc vào bài toán và cách giải quyết. Nhưng thường khi làm việc người ta để các tầng ẩn có số lượng nơ-ron bằng nhau. Ngoài ra, các nơ-ron ở các tầng thường được liên kết đôi một với nhau tạo thành mạng kết nối đầy đủ (full-connected network). Khi đó ta có thể tính được kích cỡ của mạng dựa vào số tầng và số nơ-ron. Ví dụ ở hình trên ta có:

• 4 tầng mạng, trong đó có 22 tầng ẩn
• 3+4*2+1=123+4∗2+1=12 nút mạng
• (34+44+4*1)+(4+4+1)=41(3∗4+4∗4+4∗1)+(4+4+1)=41 tham số

Bài sau chúng ta sẽ cùng tiếp tục tìm hiểu về các cách học với mạng NN