Trong phần này chúng ta sẽ tiếp tục đánh giá về Hồi quy tuyến tính (ước lượng tham số) và làm 1 ví dụ nhỏ về Hồi quy tuyến tính trong Python.

4. Ước lượng tham số

Giả sử ta có mm cặp dữ liệu huấn luyện 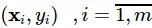được tổ chức tương ứng bằng 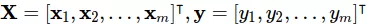và 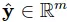là kết quả đoán tương ứng. Ta có thể đánh giá mức độ chênh lệch kết quả 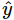và y bằng một hàm lỗi (lost function) như sau:

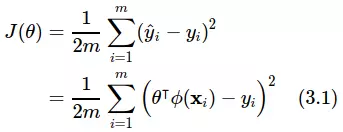
Công thức trên thể hiện trung bình của độ leehcj (khoảng cách) giữa các điểm dữa lieeyj thực tế và kết quả dự đoán sau khi ta ước lượng tham số. Hàm lỗi còn có tên gọi khác là hàm lỗi bình phương (squared error function) hoặc hàm lỗi trung bình bình phương (mean squared error function) hoặc hàm chi phí (cost function). Không cần giải thích ta cũng có thể hiểu với nhau rằng tham số tốt nhất là tham số giúp cho hàm lỗi J đạt giá trị nhỏ nhất.

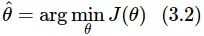
Kết quả tối ưu nhất là 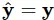, tức là 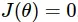. Để giải quyết bài toán này ta có thể sử dụng đạo hàm của 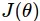và tìm 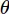sao cho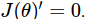

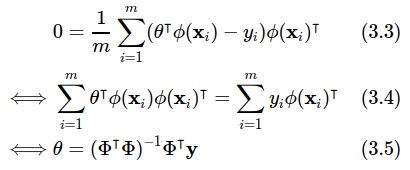
Đây chính là công thức chuẩn (normal equation) của bài toán ta cần giải. Trong đó ma trận 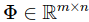được gọi là ma trận mẫu (design matrix), ta có thể hiểu nó đơn giản là tập mẫu của ta:

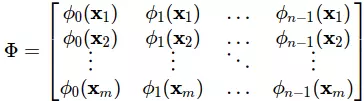
Để ý rằng ở ma trận Φ ta sắp mỗi dữ liệu huấn luyện theo hàng (m hàng) và các thuộc tính của chúng theo cột (n cột). Các thuộc tính ở đây được biến đổi bằng các hàm ϕi(xj). Và lưu ý rằng như đã đặt phía trên ϕ0(x j)=1 với mọi Ở phép lấy đạo hàm (3.3) ta thấy rằng mẫu số 2 bị triệt tiêu và giúp bỏ đi được thừa số 2 khi tính đạo hàm. Đấy chính là lý do mà người ta để mẫu số 2 cho hàm lỗi.

5. Lập trình

Ví dụ khởi động này tôi sẽ lấy dữ liệu đơn giản y = 3 + 4x để làm việc. Trước tiên tôi đã chuẩn bị tập dữ liệu huấn luyện gồm 100 cặp dữ liệu được sinh ra theo nhiễu của hàm y=3+4x.

Ở đây tôi sẽ sử dụng các thư viện pandas (xử lý dữ liệu), mathplotlib (đồ hình dữ liệu) và numpy (thao tác toán học) để làm việc:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

Dữ liệu của ta chỉ có 1 chiều nên dễ dàng đồ hình hoá, việc này cũng giúp ta ước lượng được đôi chút việc chọn các tiêu chí ràng buộc cho mô hình của ta.

# load data
df = pd.read_csv(DATA_FILE_NAME)
# plot data
df.plot(x='x', y='y', legend=False, marker='o', style='o', mec='b', mfc='w')
# expected line
plt.plot(df.values[:,0], df.values[:,1], color='g')
plt.xlabel('x'); plt.ylabel('y'); plt.show()

# extract X, y
X = df.values[:,0]
y = df.values[:,2]
# number of training examples
m = y.size

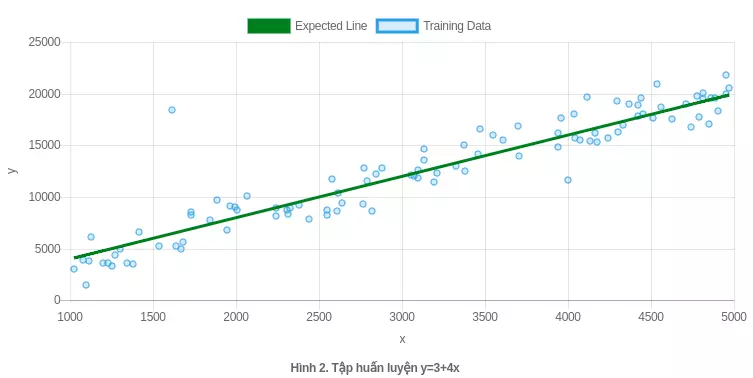
Nhìn vào biểu đồ của dữ liệu ta có thể nghĩ rằng x ở đây tuyến tính với y, tức là ta có thể chọn

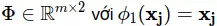
Lúc này ta sẽ có:

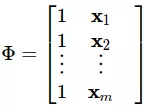
Như vậy Φ lúc này đơn giản là bằng với ma trận X có thêm cột 1 ở đầu:

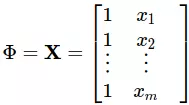Lúc này ta có thể viết lại y như sau:

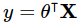
X = np.concatenate((np.ones((m,1)), X.reshape(-1,1)), axis=1)

Do (Φ ⊺Φ) có thể không khả nghịch nên ta có thể sử dụng phép giả nghịch đảo để làm việc:

theta = np.dot(np.linalg.pinv(np.dot(X.T, X)), np.dot(X.T, y))

Phép trên sẽ cho ta kết quả: theta=[-577.17310612, 4.16001358], tức:

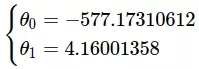
Giờ ta sẽ tính kết quả ước lượng và mô phỏng lên hình vẽ xem sao.

y_hat = np.dot(X, theta)
plt.plot(df.values[:,0], y_hat, color='r')
plt.xlabel('x'); plt.ylabel('y'); plt.show()

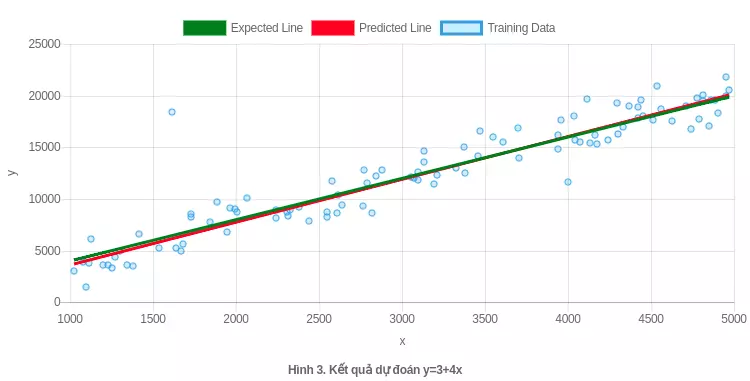
Ở hình trên, đường màu xanh là đường mà ta mong muốn đạt được còn đường màu đỏ mà mô hình ước lượng được. Như vậy ta thấy rằng θ1 khá khớp còn θ0 lại lệch rất nhiều, nhưng kết quả lại khá khớp với tập dữ liệu đang có. Nên ta có thể kì vọng rằng nếu gia tăng khoảng dữ liệu thì công thức chuẩn sẽ cho ta kết quả hợp lý hơn.

6. Kết luận

Thuật toán hồi quy tuyến tính (linear regression) thuộc vào nhóm học có giám sát (supervised learning) là được mô hình hoá bằng:

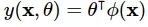
Khi khảo sát tìm tham số của mô hình ta có thể giải quyết thông qua việc tối thiểu hoá hàm lỗi (loss function):

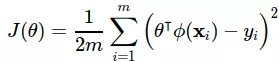
Hàm lỗi này thể hiện trung bình độ lệch giữa kết quả ước lượng và kết quả thực tế. Việc lấy bình phương giúp ta có thể dễ dàng tối ưu được bằng cách lấy đạo hàm vì nó có đạo hàm tại mọi điểm! Qua phép đạo hàm ta có được công thức chuẩn (normal equation) cho tham số:

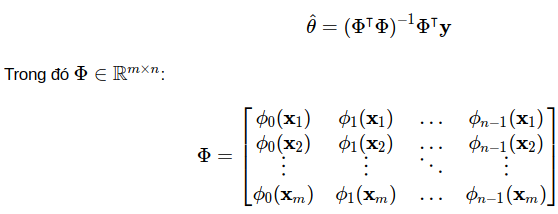
Khi lập trình với python ta có thể giải quyết việc (Φ ⊺Φ) không khả nghịch bằng cách sử dụng giả nghịch đảo để tính toán:

np.linalg.pinv(np.dot(X.T, X))

Mặc dù công thức chuẩn có thể tính được tham số nhưng với tập dữ liệu mà lớn thì khả năng sẽ không khít được với bộ nhớ của máy tính, nên trong thực tế người ta thường sử dụng phương pháp đạo hàm để tối ưu.