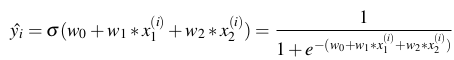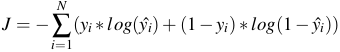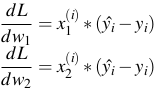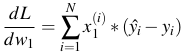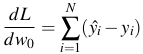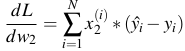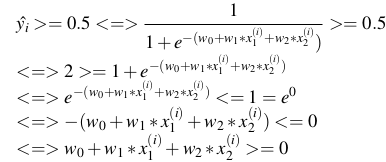1. Giới thiệu

• Trong bài viết này, chúng ta sẽ thảo luận các khái niệm Logistic Regression và xem nó có thể giúp chúng ta xử lý các vấn đề thế nào.
• Logistic Regression là 1 thuật toán phân loại được dùng để gán các đối tượng cho 1 tập hợp giá trị rời rạc (như 0, 1, 2, ...). Một ví dụ điển hình là phân loại Email, gồm có email công việc, email gia đình, email spam, ... Giao dịch trực tuyến có là an toàn hay không an toàn, khối u lành tính hay ác tình. Thuật toán trên dùng hàm sigmoid logistic để đưa ra đánh giá theo xác suất. Ví dụ: Khối u này 80% là lành tính, giao dịch này 90% là gian lận, ...

2. Đặt vấn đề

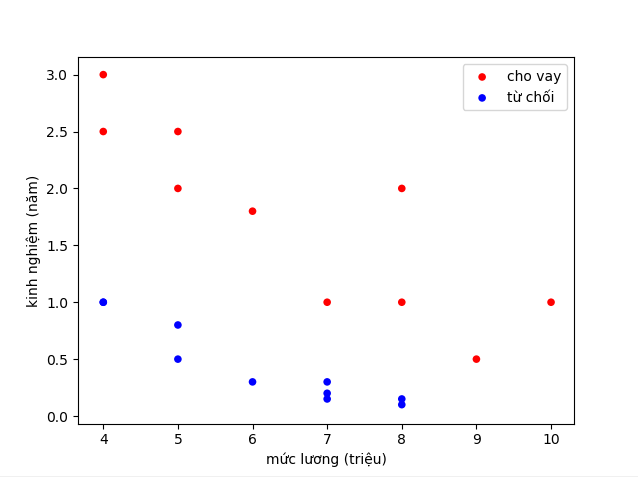
• Ngân hàng bạn đang làm có chương trình cho vay ưu đãi cho các đối tượng mua chung cư. Tuy nhiên gần đây có nhiều chung cư hấp dẫn nên lượng hồ sơ người nộp cho chương trình ưu đãi tăng lên nhiều. Bình thường bạn có thể duyệt 10-20 hồ sơ một ngày để quyết định hồ sơ có được cho vay hay không, tuy nhiên gần đây bạn nhận được 1000-2000 hồ sơ mỗi ngày. Bạn không thể xử lý hết hồ sơ và bạn cần có một giải pháp để có thể dự đoán hồ sơ mới là có nên cho vay hay không. Sau khi phân tích, bạn nhận thấy có 2 yếu tố quyết định đến việc hồ sơ có được chấp nhận hay không, đó là mức lương và kinh nghiệm làm việc. Dưới đây là 1 đồ thị ví dụ
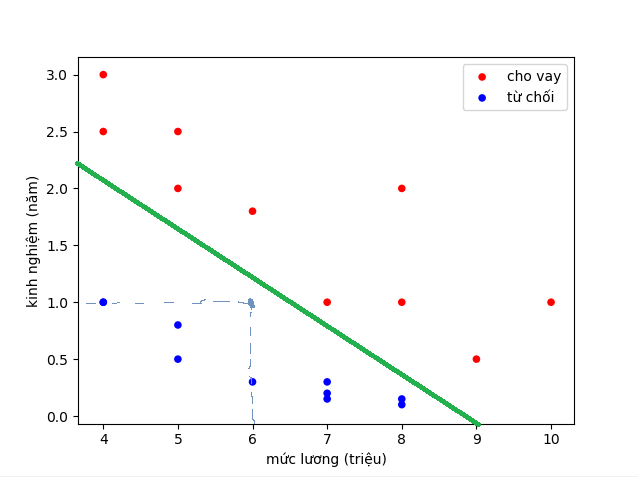
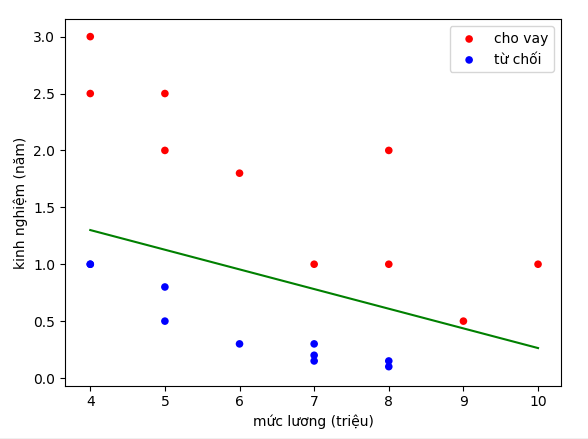
• Về mặt logic, chúng ta có thể nghĩ ngay đến việc vẽ 1 đường thẳng phân chia các điểm xanh và đó, rồi đưa ra quyết định cho 1 điểm mới dựa vào đường thẳng đó. Ví dụ thế này:
• Ví dụ đường xanh là đường phân chia. Dự đoán cho hồ sơ của người có mức lương 6 triệu và 1 năm kinh nghiệm là không chấp nhận
• Tuy nhiên, do ngân hàng đang gặp khó khăn nên hạn chế cho vay, ngân hàng yêu cầu hồ sơ đạt trên 80% mới cho vay. Bây giờ không chỉ dừng lại ở việc quyết định cho vay hay không, mà phải tìm xác suất hồ sơ đó cho vay là bao nhiêu.

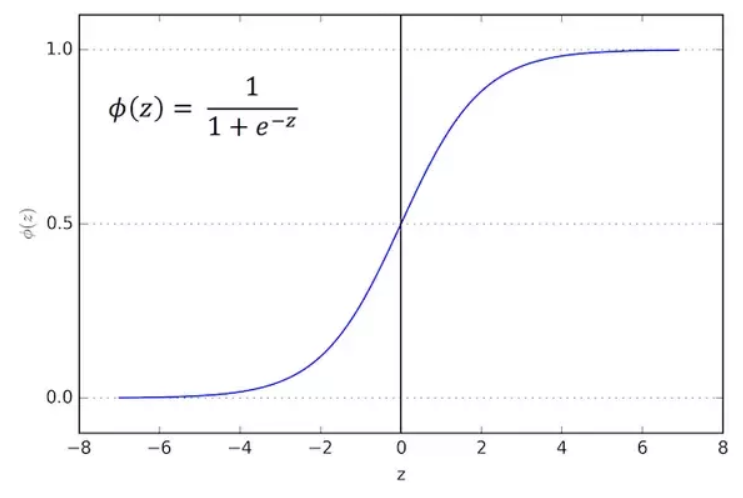
3. Hàm sigmoid

• Giờ phải tìm xác suất cho vay của 1 hồ sơ, đương nhiên là giá trị trong đoạn [0, 1] rồi. Hàm mà luôn có giá trị trong đoạn [0, 1], liên tục mà lại dễ sử dụng thì đó là hàm sigmoid.
• Nhận xét:

• Hàm liên tục và luôn đưa ra giá trị trong khoảng (0, 1)
  

• Có đạo hàm tại mọi điểm nên có thể dùng gradient descent
  

4. Thiết lập bài toán

Về cơ bản thì chúng ta sẽ có các bước sau cho 1 bài toán Machine learning:

• Thiết lập model
• Thiết lập hàm mất mát Loss Function
• Tìm tham số bằng việc tối ưu loss function
• Dự đoán dữ liệu mới dựa vào loss function mới tìm được

4.1 Model

• Với dòng thức i trong dữ liệu, gọi 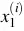là lương và là kinh nghiệm làm việc của hồ sơ thứ i
• là xác suất mà model dự đoán hồ sơ thứ i cho vay
• là xác suất mà model dự đoán hồ sơ thứ i không cho vay.
• Ta có ngay
• Hàm sigmoid là:
• Tương tự như hàm dự đoán trong Linear Regression là , thì trong Logistic Regression ta có hàm dự đoán như sau:

4.2 Loss Function - Hàm mất mát

• Bây giờ chúng ta cần 1 hàm để đánh giá độ tốt của model (tức làm dự đoán).
• Ta có nhận xét như sau: + Nếu hồ sơ thứ i là cho vay, tức = 1 thì ta mong muốn càng gần 1 càng tốt hay model dự đoán xác suất cho hồ sơ thứ i vay càng cao càng tốt. + Nếu hồ sơ thứ i là không cho vay, tức = 0 thì ta mong muốn càng gần 0 càng tốt hay model dự đoán xác suất cho hồ sơ thứ i vay càng thấp càng tốt.
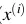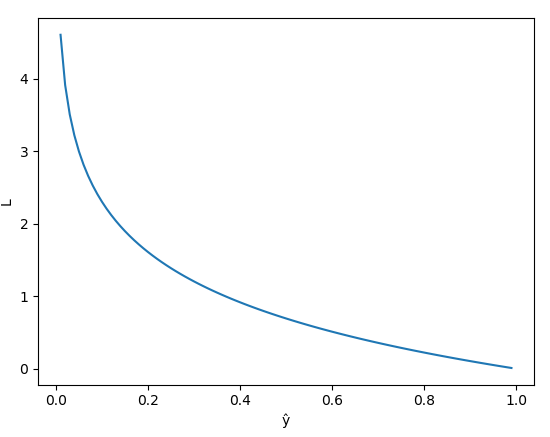
• Với mỗi điểm (, ), ta gọi hàm loss function (Trong Machine learning, Deep leaning thì chúng ta hiểu log là ln nhé)
• Thử đánh giá hàm L nhé. Nếu 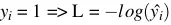. Đây là đồ thị hàm loss trong trường hợp = 1
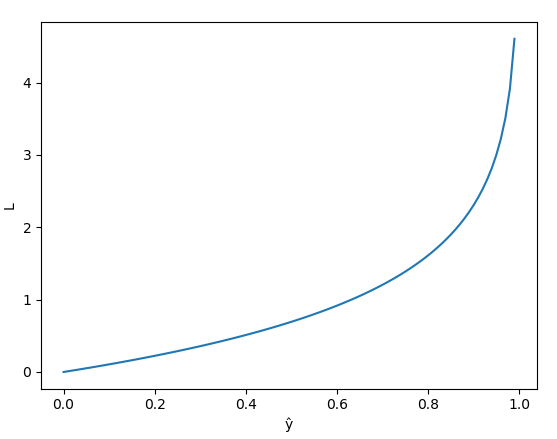
• Nhận xét: + Hàm L giảm từ 0 đến 1 + Khi model dự đoán = 1, tức giá trị dự đoán gần với giá trị thật thì L nhỏ, xấp xỉ 0. + Khi model dự đoán = 0, tức giá trị dự đoán ngược lại với giá trị thật thì L rất lớn.
• Ngược lại, nếu , ta có đồ thị sau
• Nhận xét: + Hàm L tăng từ 0 đến 1 + Khi model dự đoán gần 0, tức giá trị dự đoán gần với giá trị thật thì L nhỏ, xấp xỉ 0. + Khi model dự đoán gần 1, tức giá trị dự đoán ngược lại với giá trị thật thì L rất lớn => Hàm L nhỏ khi giá trị model gần với giá trị thật và rất lớn khi model dự đoán sai, hay nói cách khác L càng nhỏ thì model dự đoán càng gần với giá trị thật. => Bài toán toán quy về tìm giá trị nhỏ nhất của L.
• Ta có hàm mất mát trên tất cả bộ dữ liệu như sau:

4.3 Tính đạo hàm phức tạp bằng kỹ thuật Chain Rule

• Chain rule là gì? Nếu z = f(y) và y = g(x) hay z = f(g(x)) thì
• Thử áp dụng tính đạo hàm của hàm sigmoid . =

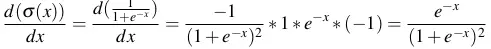4.4 Áp dụng gradient descent

• Với mỗi điểm (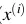, ), gọi hàm mất mát trong đó là giá trị mà model dự đoán, còn yi là giá trị thật của dữ liệu.
• Áp dụng Chain rule ta có:
• Từ đồ thị ta thấy: Do đó:
• Tương tự:
• Đấy là trên 1 điểm dữ liệu, còn trên toàn bộ dữ liệu:

4.5 Biểu diễn bằng ma trận

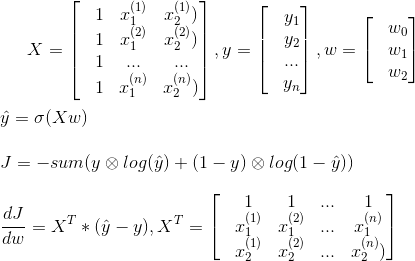
• Sau khi thực hiện gradient descent ta tìm được w0, w1, w2. Với mỗi hồ sơ mới 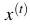ta tính được phần trăm nên cho vay 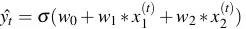rồi so sánh với ngưỡng cho vay của công ty t (thường là 0.5, hoặc cao hơn là 0.8), nếu thì cho vay, không thì không cho vay.

4.6 Xây dựng đường thẳng phân chia

• Xét đường thẳng y = ax + b, thì f = y - (ax + b), ta có được 1 đường thẳng chia mặt phẳng là 2 phần, 1 phần f > 0, 1 phần f < 0 và các điểm trên đường thẳng thì f = 0.
• Giả sử mốc chính giữa là 0.5 thì >= 0.5 thì cho vay, ngược lại thì không cho vay.
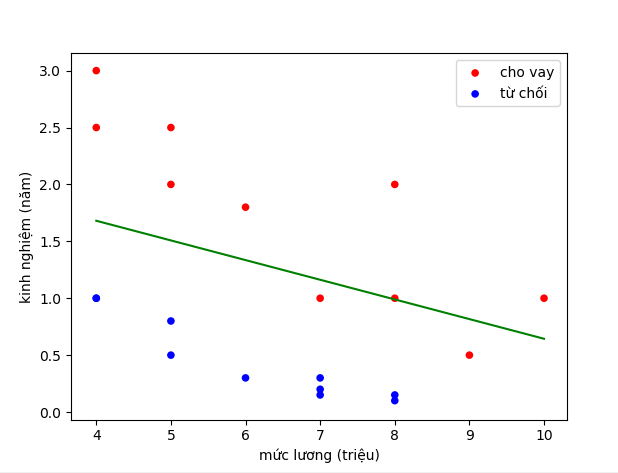
• Tương tự => đường thẳng là đường phân cách giữa các điểm cho vay và từ chối.
• Trong trường hợp tổng quát t bất kỳ, <=>
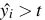• Ta thấy khi t = 0.8 thì đường phân cách gần các điểm màu đỏ hơn so với t = 0.5, thậm chí 2 điểm màu đỏ trước đó được chấp nhận thì bây giờ lại bị loại bỏ.

5. Ứng dụng

• Dự đoán email có phải spam hay không
• Dự đoán giao dịch ngân hàng là gian lận hay không
• Dự đoán khối u lành hay ác tính
• Dự đoán khoản vay có trả được không
• Dự đoán khoản đầu tư vào start-up có sinh lãi hay không.

Nguồn Towards Datascience, Deep learning cơ bản