Machine Learning, Deep Learning cho người bắt đầu: Thư viện Numpy và TensorFlow
Bài đăng này đã không được cập nhật trong 6 năm
Trong bài trước của series Machine Learning, Deep Learning cho người bắt đầu, chúng ta đã tìm hiểu qua về Mảng NumPy - NumPy Array trong Python. Cùng điểm lại các kiến thức liên quan ở bài trước và tìm hiểu thêm về các APIs của thư việc Numpy
I. Numpy
I.I Giới thiệu về NumPy
- Trang chủ của NumPy
- NumPy là viết tắt của "Numerical Python", là một thư viện chuyên để xử lý, tính toán vector, ma trận.
- NumPy thường được sử dụng cùng SciPy và Matplotlib để thay thế cho MatLab vô cùng đắt đỏ.
- Được viết bằng Python và C nên tốc độ thực thi tốt.
I.2 Các APIs
1. Mảng NumPy - NumPy Array
2. Truy cập thông qua chỉ mục và cắt Array - Array Indexing và Array Slicing
a. Indexing và Slicing
indexing và Slicing tương tự với list trong Python.
Phần này rất nhiều cách làm nhưng tôi chỉ trình bày các cách dễ hiểu và thực tế hay dùng nhất.
Bạn có thể tham khảo chi tiết tại đây
- Indexing cơ bản
import numpy as np
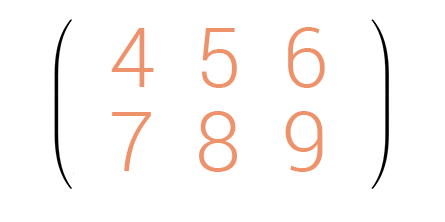
Mảng 2 chiều. Chúng ta có thể liên tưởng đến ma trận 2 chiều.
Việc mô phỏng ma trận nhiều chiều của NumPy dựa trên việc sử dụng list bên trong list (nested list) cho nên việc truy cập các phần tử trong mảng này hoàn toàn tương tự như chúng ta đã thực hiện trong Python.
Input:
number_2D = np.array([[4,5,6], [7, 8, 9]])
number_2D
Output:
array([[4, 5, 6],
[7, 8, 9]])
Input:
number_2D.shape
Output:
(2, 3)
Truy cập hàng
Truy cập hàng đầu tiên của ma trận
Input:
number_2D[0]
Output:
array([4, 5, 6])
Truy cập hàng cuối cùng của ma trận
Input:
number_2D[-1]
Output:
array([7, 8, 9])
Truy cập cột
Truy cập cột đầu tiên của ma trận: việc này tương đương với truy cập tất cả các hàng và lấy phần tử đầu tiên.
Input:
number_2D[:, 0] # -> Dấu : biển hiện việc duyệt qua tất cả các hàng, qua mỗi hàng ta lấy phần tử đầu tiên
Output:
array([4, 7])
Truy cập cột cuối cùng của ma trận
Input:
number_2D[:, -1]
Output:
array([6, 9])
Truy cập cột giữa của ma trận
Input:
number_2D[:, 1]
Output:
array([5, 8])
Truy cập mảng trong ma trận
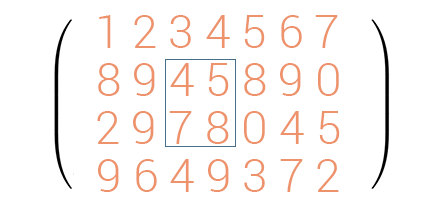
Input:
awesome = np.array([
[1, 2, 3, 4, 5, 6, 7],
[8, 9, 4, 5, 8, 9, 0],
[2, 9, 7, 8, 0, 4, 5],
[9, 6, 4, 9, 3, 7, 2],
])
awesome.shape # -> Một ma trận 4 hàng 7 cột
Output:
(4, 7)
Các bước tiến hành
- Truy cập hàng 2 và hàng 3 thông qua chỉ mục 1 và 2
- Truy cập cột 2 và cột 3 của 2 hàng trên thông qua chỉ mục 2 và 3
Input:
awesome[1:3, 2:4]
Output:
array([[4, 5],
[7, 8]])
Truy cập phần tử
Truy cập phần tử
 Các bước tiến hành:
Các bước tiến hành:
- Truy cập hàng 1 thông qua chỉ mục là 0
- Truy cập phần tử cột 2 hàng 1 thông qua chỉ mục là 1
Input:
awesome[0, 1]
Output:
2
# Tương đương với
awesome[0][1]
Truy cập phần tử hàng 2 cột 3
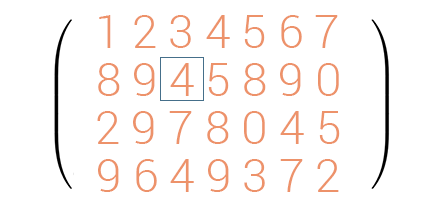
Các bước tiến hành:
- Truy cập hàng 2 thông qua chỉ mục là 1
- Truy cập phần tử cột 3 hàng 2 thông qua chỉ mục là 2
Input:
awesome[1, 2]
Output:
4
# Tương đương với
awesome[1][2]
3. Phép lan truyền - Broadcasting
Xem kỹ về Broadcasting
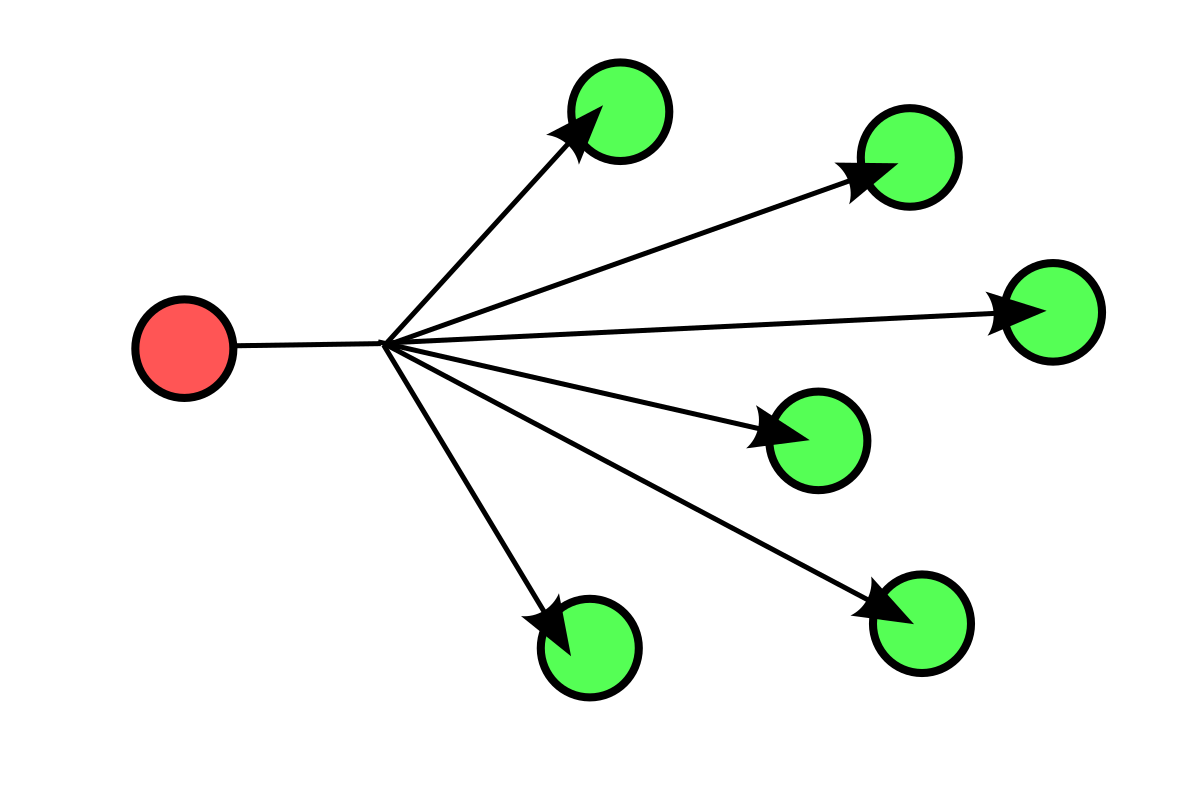
Boardcasting chúng ta có thể dịch là lan truyền, cách mà chúng ta thay đổi đồng loạt giá trị nhiều phần tử của mảng. Cụ thể hơn nữa Numpy cho phép thực hiện tính toán giữa các mảng với số và các mảng khác chiều với nhau.
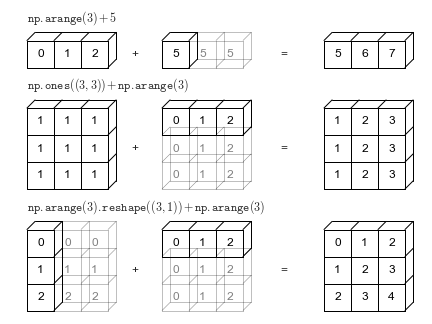
Nguồn ảnh: Python Data Science Handbook - Jake VanderPlas
a. Lan truyền mảng với số
Phép cộng mảng với số
Mảng một chiều
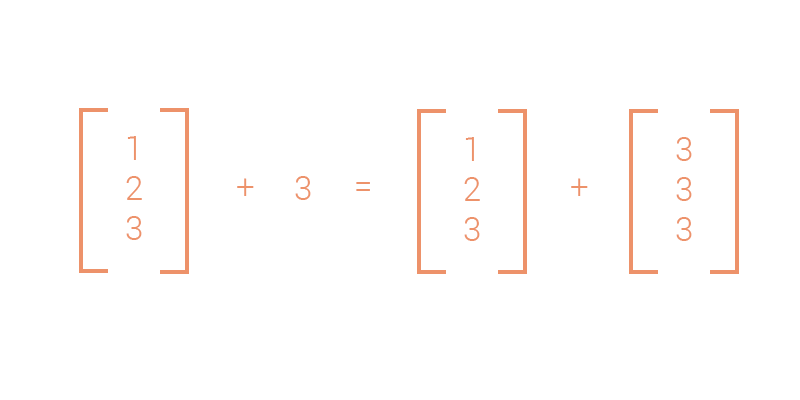
Input:
import numpy as np
numbers_1D = np.array([1, 2, 3])
numbers_1D + 3
Output:
array([4, 5, 6])
Như chúng ta thấy ở bên trên, 3 được cộng với tất cả (broadcasting) phần tử của x.
Một cách liên tưởng đơn giản giống dòng đầu tiên hình 2, Numpy đã chuyển số 3 thành một array một chiều là [3, 3, 3] để thực hiện phép cộng này.
# Tương đương với
numbers_1D + np.array([3, 3, 3])
array([4, 5, 6])
# Tương tự với phép trừ
numbers_1D + 3 - 10
array([-6, -5, -4])
Mảng hai chiều
Input:
numbers_2D = np.asarray([
[4, 5, 6],
[7, 8, 9]
])
numbers_2D + 20
array([[24, 25, 26],
[27, 28, 29]])
Phép nhân mảng với số
Mảng một chiều
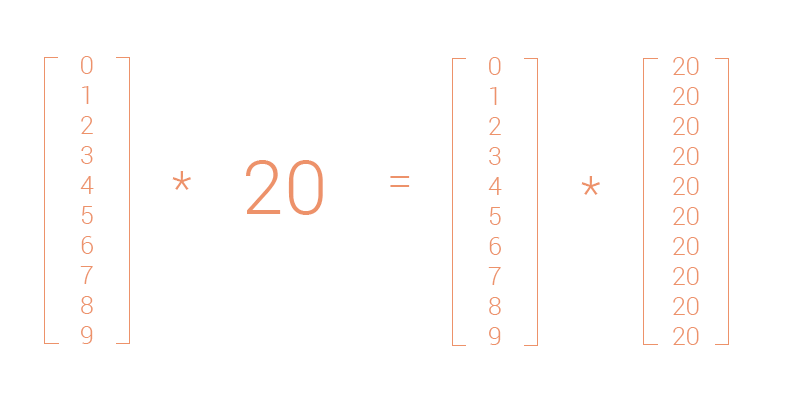
Input:
numbers_1D_range = np.arange(10)
numbers_1D_range
Output:
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
Input:
numbers_1D_range * 20
Output:
array([ 0, 20, 40, 60, 80, 100, 120, 140, 160, 180])
Mảng hai chiều
Input:
numbers_2D_ones = np.ones((10, 10))
numbers_2D_ones
Output:
array([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])
Input:
numbers_2D_ones * 8
array([[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.],
[8., 8., 8., 8., 8., 8., 8., 8., 8., 8.]])
b. Lan truyền mảng với mảng
Phép cộng 2 mảng khác chiều
Mảng 2 chiều với mảng 1 chiều
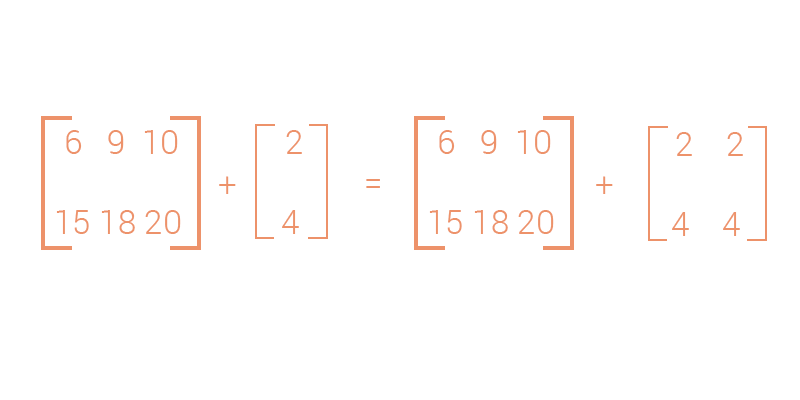
Input:
x = np.array([
[6, 9, 10],
[15, 18, 20],
])
y = np.array([
[2],
[4],
])
x + y
array([[ 8, 11, 12],
[19, 22, 24]])
Còn nữa ...
All rights reserved