Perceptron Learning Algorithm
Bài đăng này đã không được cập nhật trong 6 năm
1 Giới thiệu
1.1 Bài toán phân loại (classification)
Giả sử chúng ta cần chia khách hàng ra làm hai loại/lớp (category/class) dựa vào nguồn lợi họ đem lại cho công ty: khách hàng nhỏ và khách hàng lớn. Về cơ bản, nguồn lợi được tính theo giá mặt hàng và số lượng khách mua. Như vậy, ta sẽ biểu diễn khách hàng theo hai yếu tố trên trên mặt phẳng:
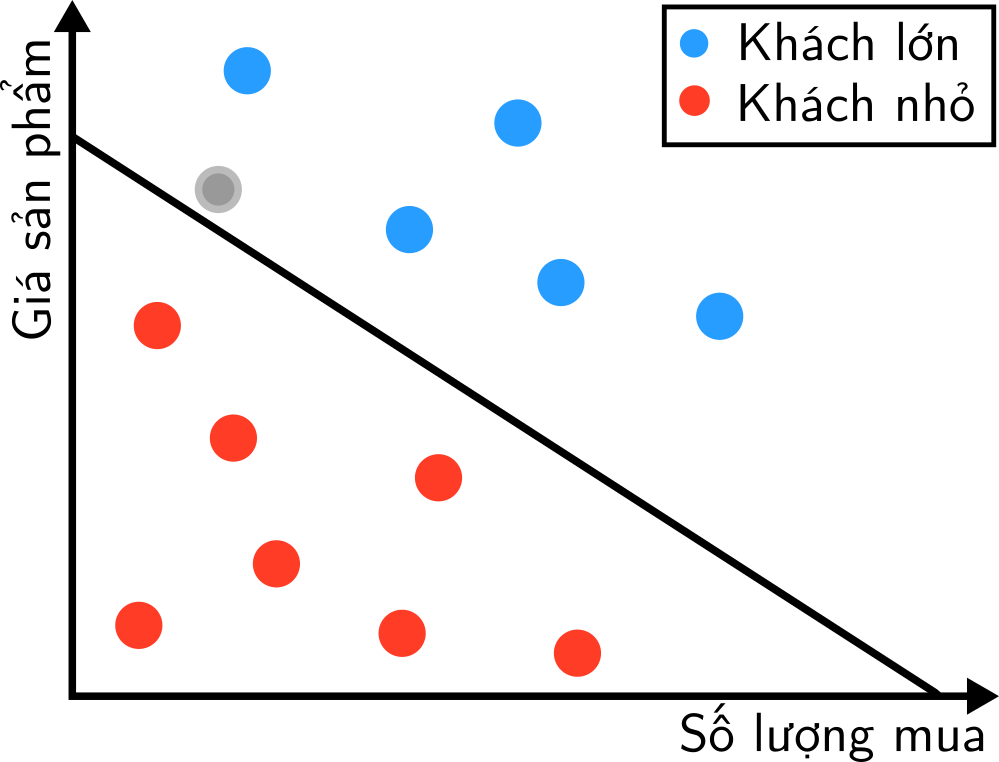
Bài toán của chúng ta là từ những điểm xanh và đỏ cho trước (tức marketer đã xác định), hãy xây dựng một quy tắc phân loại để dự đoán class của điểm màu xám. Nói cách khác, chúng ta cần xác định một biên giới để chia lãnh thổ của hai class này, rồi với điểm cần phân loại màu xám ta chỉ cần xem nó nằm ở phía bên nào của đường biên giới là xong. Biên giới đơn giản nhất (theo đúng nghĩa toán học) trong mặt phẳng là một đường thằng (đường màu đen trong hình), trong không gian ba chiều là một mặt phẳng, trong không gian nhiều chiều là một siêu phẳng (hyperplane, một đường thẳng nằm trong nhiều chiều).
Lưu ý rằng các khái niệm lớp, nhãn, danh mục ở bài toán phân loại là tương tự nhau.
1.2 Perceptron
Perceptron Learning Algorithm, gọi ngắn là Perceptron, là một thuật toán giúp chúng ta thực hiện công việc phân loại với hai lớp như trên, ta sẽ gọi hai lớp này là {+1, -1}. Thuật toán ban đầu được Frank Rosenblatt đề xuất dựa trên ý tưởng của Neural thần kinh, nó nhanh chóng tạo nên tiếng vang lớn trong lĩnh vực AI. Không giống như Naive Bayes - một thuật toán phân loại bằng cách tính xác xuất trên toàn bộ tập dữ liệu (batch learning), Perceptron sẽ đọc từng dữ liệu và điều chỉnh biên giới sao cho tất cả các điểm nằm cùng một phía của biên giới có nhãn giống nhau (online learning).
1.3 Linear Separability
Một nhược điểm của Perceptron là nó chỉ hoạt động thực sự tốt khi dữ liệu phân tách tuyến tính (linearly separable), tức có thể dùng đường thẳng, mặt phẳng, siêu phẳng để làm biên giới, nếu dữ liệu không thỏa điều kiện này, không những Perceptron mà bất kì thuật toán phân loại tuyến tính nào cũng sẽ fail "nhè nhẹ". Điều này dẫn đến một khái niệm quan trọng:
Linear separability: cho vector biểu diễn một dữ liệu, là nhãn của và là feature function của dữ liệu, tập dữ liệu này được gọi là linearly separable nếu tồn tại một vector trọng số và một margin sao cho:
với khác , là nhãn của lớp còn lại. Điều này khá dễ hiểu vì khi cùng dấu với , tức phân lớp đúng, thì tích của chúng không âm.
Ví dụ ta có vector trọng số và vector có nhãn , như vậy thay vào công thức trên ta được:
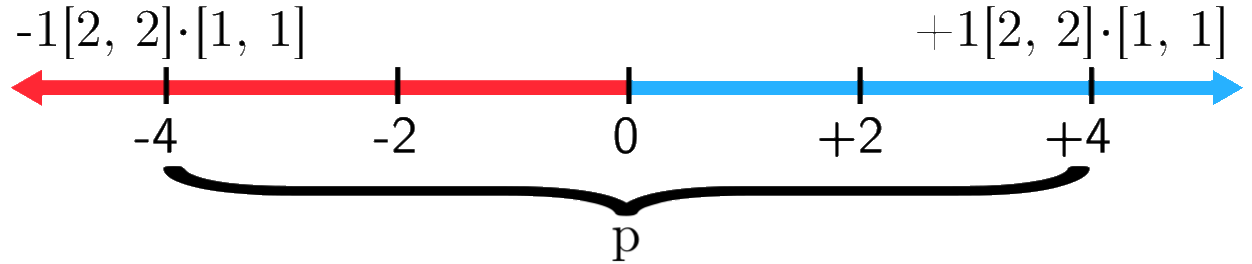
Nói cách khác, dữ liệu là linearly separable khi hai tập bao lồi các điểm của hai lớp không giao nhau.
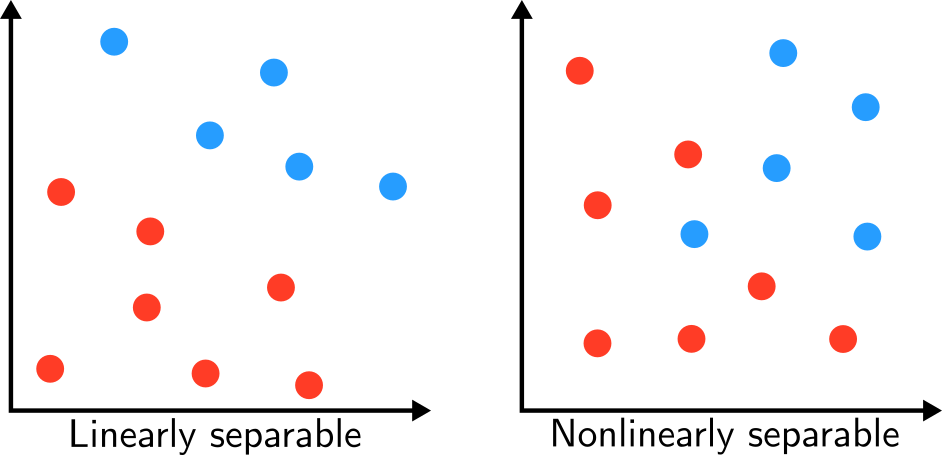
Dữ liệu trên thực tế thường hiếm khi linearly separable là một hạn chế cho Perceptron, tuy nhiên Perceptron vẫn là nền tảng cho các thuật toán Neural Network hay Deep Learning sau này.
2 Thuật toán Perceptron
2.1 Ý tưởng
 Chúng ta có đường nét đứt là biên giới phân lớp. Thuật toán sẽ dùng đường biên giới để thử phân loại dữ liệu, với mỗi lần phân loại thử bị sai, thuật toán sẽ điều chỉnh lại biên giới. Ở hình bên trái, có một điểm xanh nằm cùng lãnh thổ với các điểm màu đỏ, do đó nó bị thuật toán phân loại sai. Thuật toán sẽ "xoay" biên giới về phía điểm xanh ấy sao cho điểm này thuộc về lãnh thổ của các điểm xanh.
Chúng ta có đường nét đứt là biên giới phân lớp. Thuật toán sẽ dùng đường biên giới để thử phân loại dữ liệu, với mỗi lần phân loại thử bị sai, thuật toán sẽ điều chỉnh lại biên giới. Ở hình bên trái, có một điểm xanh nằm cùng lãnh thổ với các điểm màu đỏ, do đó nó bị thuật toán phân loại sai. Thuật toán sẽ "xoay" biên giới về phía điểm xanh ấy sao cho điểm này thuộc về lãnh thổ của các điểm xanh.
2.2 Cơ sở toán học
2.2.1 Vector trọng số và biên giới
Ở phần 1.3 ta đã đề cập:
Vì nên
Và vì trái dấu và vế trái của luôn lớn hơn vế phải, nên vế trái của không âm và vế phải luôn âm
Ta có hàm của hai vector:
Quay về , với vế trái là tích của hai vector và là không âm ta có:
Vế bên phải cũng tương tự:
Gọi là góc giữa hai vector và . Ở , nên nằm trong đoạn . Tương tự với , góc giữa và là nằm trong khoảng . Như vậy các feature vector và phải hợp với một góc lần lượt là và , ta hình dung được lãnh thổ của mỗi class:

vuông góc với biên giới phân lớp. Do đó với mọi vector nằm cùng lãnh thổ chia bởi biên giới thì tích vô hướng của chúng với không trái dấu với các vector khác trong cùng lãnh thổ, tất cả đều thuộc về một class. Khi vector xoay bao nhiêu thì biên giới cũng xoay bấy nhiêu để đảm bảo chúng vuông góc nhau, đây là câu trả lời tại sao quyết định biên giới phân lớp.
2.2.2 Cập nhật
Việc cập nhật sẽ diễn ra khi thuật toán đoán sai nhãn của dữ liệu học. Khi phải đoán một điểm dữ liệu, thuật toán không hề biết trước nhãn/lớp của nó, dữ liệu đoán mặc định có feature vector là tích của vector biểu diễn dữ liệu đó với .
Chúng ta có hai trường hợp phải cập nhật:
- Khi nhãn dữ liệu là +1 và đoán thành -1.
- Khi nhãn dữ liệu là -1 và đoán thành +1.
Ta sẽ xem xét trường hợp đầu tiên, và . Ở phần trên đã đề cập, khi dự đoán đúng nhãn :
Vì nên để thỏa (4), thì . Nhưng vì dự đoán sai nên hiện tại , dẫn đến không thỏa . Cũng có:
Mục đích cập nhật ở trường hợp này là điều chỉnh lại sao cho:
Lưu ý: ta không cần để ý đến đoạn , vì nó cũng tương tự với đoạn .
Vậy phải điều chỉnh làm sao để ? Ta có quy tắc hình bình hành:
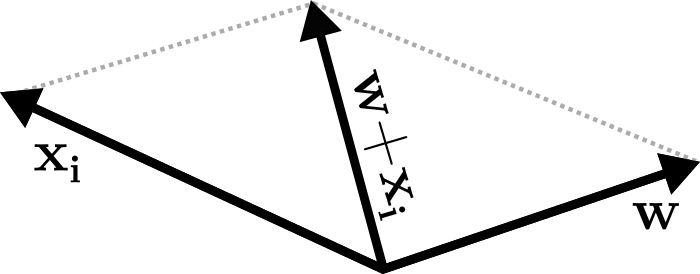
Đường chéo của hình bình hành, tức sẽ luôn hợp với một góc không lớn hơn ! Như vậy công thức cập nhật khi nhãn dữ liệu là +1 và đoán sai thành -1 là:
Suy luận tương tự với trường hợp nhãn dữ liệu là -1 và đoán sai thành +1, công thức cập nhật:
Ta có công thức cập nhật tổng quát mỗi khi thuật toán đoán sai, với là nhãn chính xác của dữ liệu:
2.3 Thuật toán
Thuật toán được viết gọn như sau:
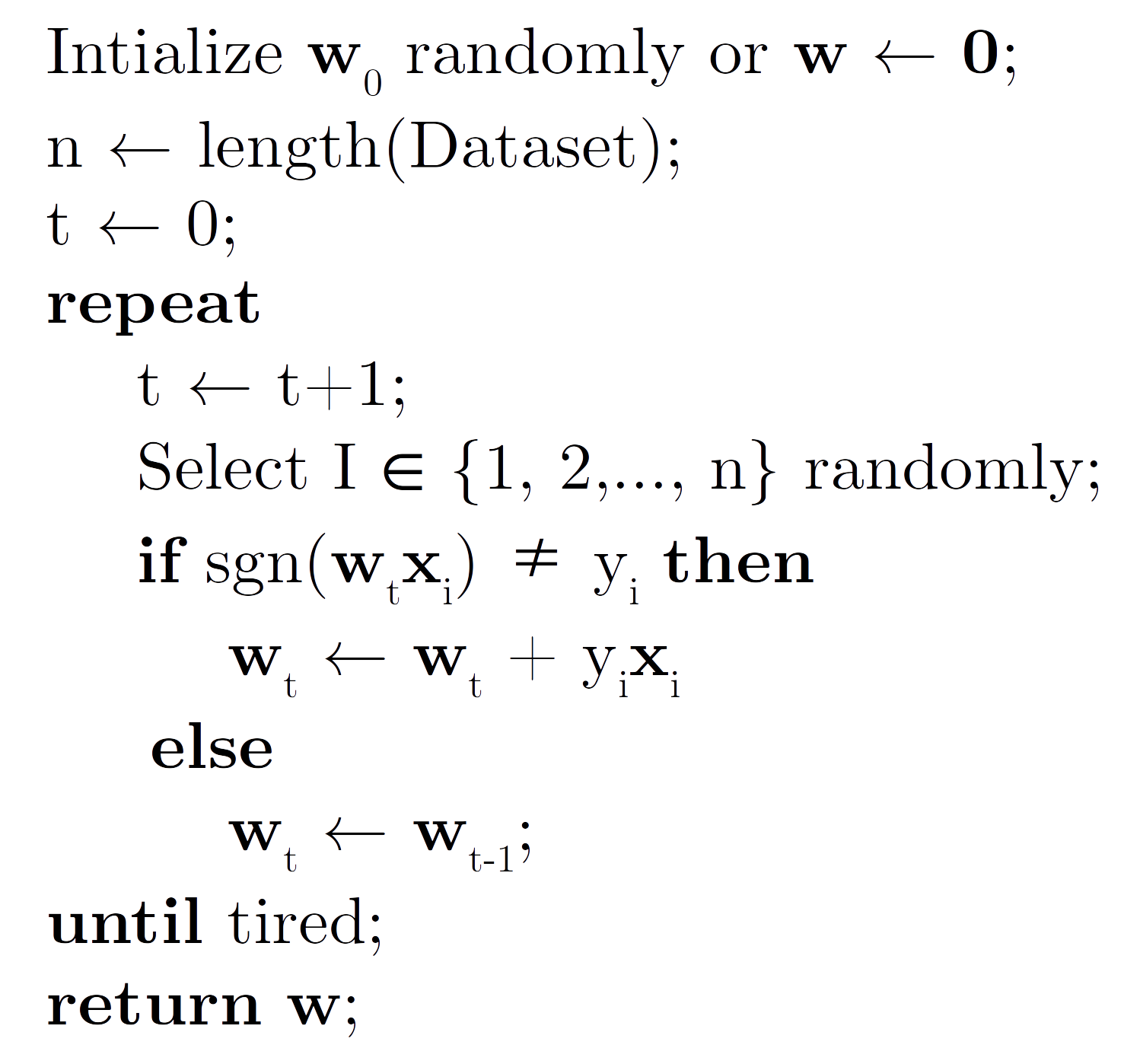
Với hàm nếu và nếu .
2.4 Averaged Perceptron
Nếu dữ liệu linearly separable, Perceptron sẽ dừng lại một khi tìm được biên giới phân loại chính xác, còn không nó sẽ luẩn quẩn giữa các trọng số mà không hội tụ lại. Một giải pháp cho trường hợp này là ta sẽ cộng các vector ở cuối mỗi lần lặp, rồi chia nó cho số lần lặp, thuật toán chắc chắn hội tụ. Ta xem xét nếu trọng số trung bình giữa các vòng lặp chênh nhau ở một ngưỡng nào đó thì có thể cho dừng. Việc tính trọng số trung bình được chứng minh là làm cho mô hình có tính tổng quát. Tuy nhiên cách làm này tốn rất nhiều chi phí hơn "bản gốc" .
Một cách khác là ta sử dụng một tập kiểm tra ở ngoài, khi độ chính xác trên tập này bắt đầu giảm, có thể thuật toán đang dần overfit và ta dừng ở đây. Cách làm này gọi là early stopping.
Chúng ta vừa tìm hiểu một thuật toán nền tảng cho Neural Network, hi vọng bạn đọc phần nào hình dung được cách làm việc của nó. Bài viết nhiều toán và khô khan như thế này khó tránh khỏi sai sót, mong mọi người đóng góp ý kiến 
All rights reserved