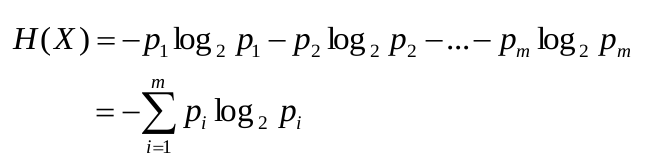Decision Tree

Decision tree là một mô hình supervised learning, có thể được áp dụng vào cả hai bài toán classification và regression. Mỗi một nút trong (internal node) tương ứng với một biến; đường nối giữa nó với nút con của nó thể hiện một giá trị cụ thể cho biến đó. Mỗi nút lá đại diện cho giá trị dự đoán của biến mục tiêu, cho trước các giá trị của các biến được biểu diễn bởi đường đi từ nút gốc tới nút lá đó. Kỹ thuật học máy dùng trong cây quyết định được gọi là học bằng cây quyết định, hay chỉ gọi với cái tên ngắn gọn là cây quyết định.

1. Entropy

Giả sử ta có biến ngẫu nhiên rời rạc X:

• Có không gian mẫu là {x₁, x₂, ..., x_m} với xác suất
• P(X = x₁) = p₁, P(X = x₂) = p₂, ..., P(X = x_m) = p_m Số bit trung bình nhỏ nhất để truyền một đơn vị dữ liệu theo phân phối P(X):

H(X) là entropy của X (0 <= H(X) <= log₂m)
Xem xét m = 2, trong trường hợp X là tinh khiết nhất, tức là một trong hai p_i bằng 0 và giá trị kia bằng 1, khi đó H(X) = 0. Khi X là vẩn đục nhất tức cả hai xác suất mang giá trị p_i = 0.5, hàm entropy đạt giá trị cao nhất.

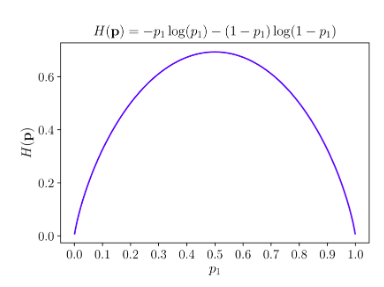
Vậy với m > 2,hàm entropy đạt giá trị nhỏ nhất nếu có một giá trị p_i = 1 (tức các giá trị pi còn lại mang giá trị 0), đạt giá trị lớn nhất nếu tất cả pi bằng nhau.
Giá trị entropy:

• Lớn: Phân phối P(X) gần với dạng phân phối đồng nhất (uniform distribution)
• Nhỏ: Phân phối P(X) xa dạng phân phối đồng nhất
  Những giá trị này khiến nó được sử dụng trong việc đo độ vẩn đục của một pháp phân chia trong ID3 (Hôm bữa kiểm tra nói sai phần này ). Nên ID3 còn được gọi là entropy-based descision tree.

Entropy điều kiện H(Y|X)

H(Y|X) = trung bình các giá trọ entropy điều kiện cụ thể H(Y|X = v)

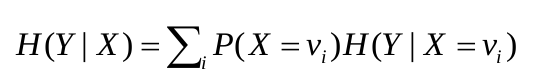
Ví dụ:

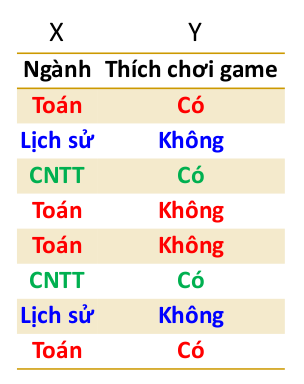
Ta có:

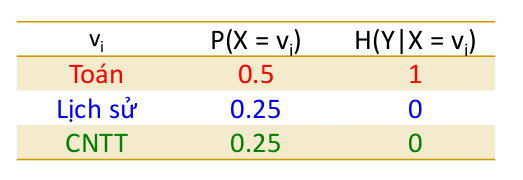
Vậy nên: H(Y|X) = 0.5 x 1 + 0.25 x 0 + 0.25 x 0 = 0.5

Information Gain IG(Y|X)

IG(Y|X) là số lượng bit trung bình có thể tiết kiệm khi truyền Y mà hai đầu gửi và nhận đã biết X.
Tức là: IG(Y|X) = H(Y) - H(Y|X)

Ví dụ:
H(Y) = 1
H(Y|X) = 0.5
IG(Y|X) = 1 - 0.5 = 0.5

2. Iterative Dichotomiser 3 (ID3)

Input:

Tập dữ liệu huấn luyện D
Tập các lớp C = {c₁, c₂, ..., c_n} là thuộc tính đích.
Attributes = F tập toàn bộ các thuộc tính điều kiện

ID3

1. Tạo nốt gốc (root) cho cây.

2. Nếu tất cả các đối tượng x thuộc D có cùng một lớp c_k, trả về nốt gốc Root với nhãn c_k.

3. Nếu không còn thuộc tính điều kiện nào (Attributes = rỗng), trả về nốt gốc Root với nhãn c_k nào xuất hiện nhiều nhất trong D.

4. Nếu không thì:

   4.1. Chọn thuộc tính F_i thuộc Attributes là thuộc tính phân lớp tốt nhất (với thuận toán ID3 là thuộc tính phân lớp tốt nhất là thuộc tính có độ lợi thông tin lớn nhất) cho tập D làm nốt gốc.

   4.2. Đối với mỗi giá trị vⁱ_j của Fi 4.2.1. Thêm một nhánh dưới nốt root tương ứng với F_i = vⁱ_j.
   4.2.2. D(vⁱ_j) là tập các đối tượng thuộc D có F_i= vⁱ_j
   4.2.3. Nếu D(vⁱ_j) = rỗng, thêm một nốt lá (leaf node) dưới nhánh này với nhãn ck nào đó phổ biến nhất trong D. Ngược lại dưới nhánh này thêm một cây con ID3(D(vⁱ_j), C, Attributes - {F_i})
   

5. Trả về nốt gốc Root.

Ví dụ

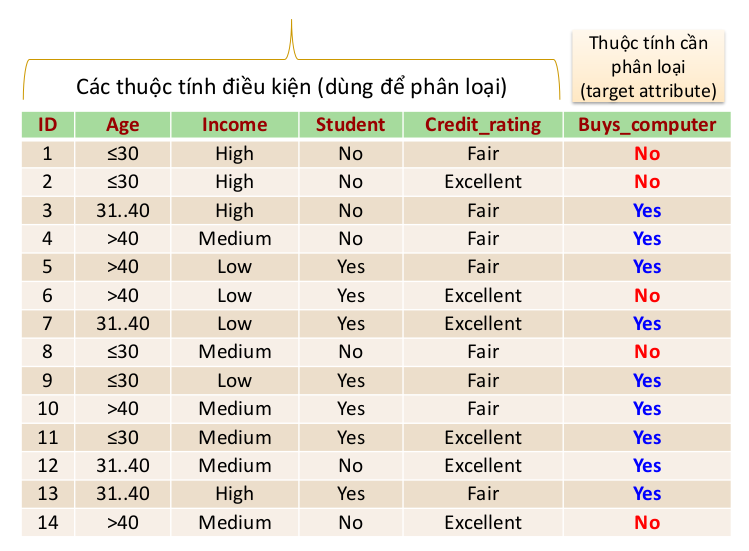
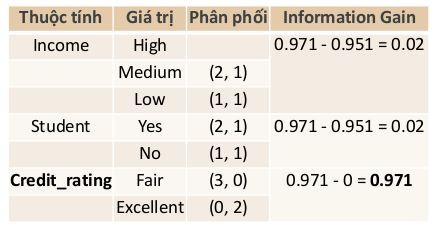
Information Gain theo từng thuộc tính.

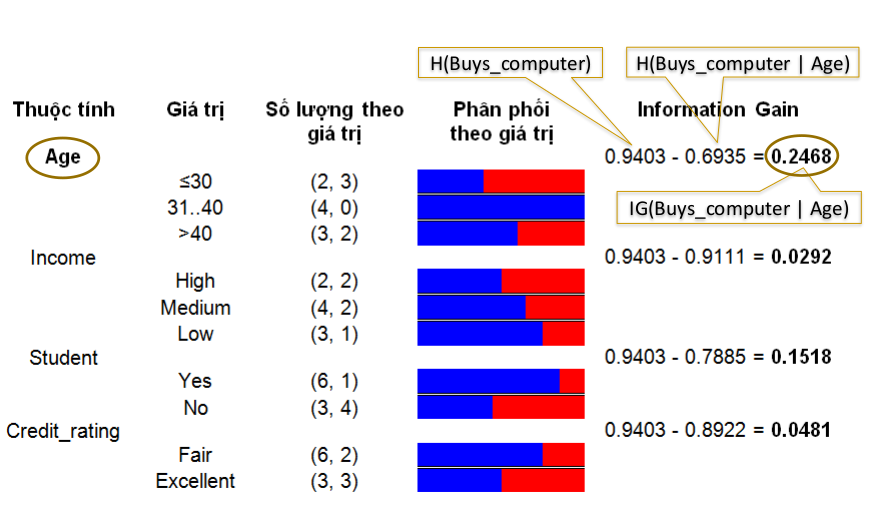
Dựng cây với nốt là thuộc tính Age.

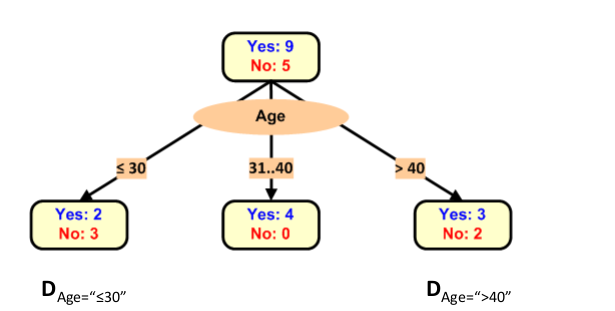
Tiếp tục tính Information Gain cho những thuộc tính còn lại:

Tiếp tục dựng cây:

3. Thuật toán C4.5

C4.5 là thuật toán cải tiến so với ID3:

• Sử dụng Gain Ratio (thay vì Information Gain) để chọn thuộc tính phân chia trong quá trình dựng cây.
• Xử lý tốt cả hai dạng thuộc tính: rời rạc, liên tục
• Xử lý dữ liệu không đầy đủ (thiếu một số giá trị tại một số thuộc tính).

• C4.5 cho phép các thuộc tính - giá trị bị thiếu có thể thay bằng dấu hỏi (?)
• Những giá trị bị thiếu không được xem xét khi tính toán Information Gain và Gain Radio

• Cắt tỉa cây sau khi xây dựng: Loại bỏ những nhánh cây không thực sự ý nghĩa (thay bằng nốt lá).

Ý nghĩa của Gain Ratio (GR)

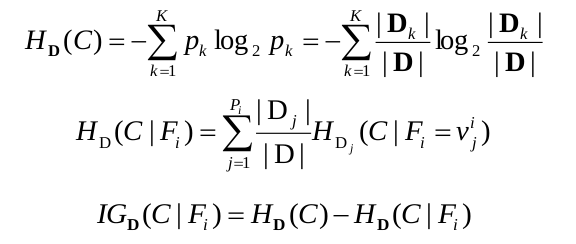
Spliting entropy của thuộc tính Fi, ký hiệu SE(Fi):

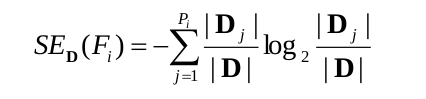
Khi đó, Gain Ratio ký hiệu GR_D(C|F_i)

Giá trị Information Gain và Gain Ratio

1. Tiêu chí Information Gain thường "ưu tiên" chọn những thuộc tính có nhiều giá trị (miền xác định lớn)
2. Spliting entropy, SE_D(F_i) sẽ lớn khi thuộc tính F_i có nhiều giá trị. Điều này giúp:
   2.1. Làm giảm Gain Ratio của thuộc tính có nhiều giá trị.
   2.2 Làm tăng Gain Ratio của thuộc tính có ít giá trị.
   
3. Ý nghĩa khác:
   Giảm vấn đề "quá khớp"

4. Kết luận

Ưu điểm

• Mô hình dễ hiểu và dễ giải thích.
• Cần ít dữ liệu để huẩn luyện.
• Có thể xử lý tốt với dữ liệu dạng số (rời rạc và liên tục) và dữ liệu hạng mục.
• Mô hình dạng white box rõ ràng.
• Xây dựng nhanh.
• Phân lớp nhanh.

Nhược điểm

• Không đảm bảo xây dựng được cây tối ưu.
• Có thể overfitting (tạo ra những cây quá khớp với dữ liệu huấn luyện hay quá phức tạp).
• Thường ưu tiên thuộc tính có nhiều giá trị (khắc phục bằng các sử dụng Gain Ratio).

5. Ứng dụng

• Xử lý tốt dữ liệu dạng bảng biếu với số thuộc tính không quá lớn.
• Không phù hợp khi số lượng thuộc tính bùng nổ (như dữ liệu văn bản, hình ảnh, âm thanh, video, ...).

Bài viết tham khảo bài giảng của thầy Phan Xuân hiếu - Giảng viên trường đại học Công Nghệ