Linear Regression

Hồi quy tuyến tính có lẽ là một trong những thuật toán nổi tiếng và được hiểu rõ nhất trong thống kê và học máy. Trong bài đăng này, bạn sẽ khám phá thuật toán hồi quy tuyến tính, cách nó hoạt động và cách bạn có thể sử dụng nó tốt nhất trong các dự án máy học của mình. Trong bài đăng này, bạn sẽ học:

• Tại sao hồi quy tuyến tính thuộc về cả thống kê và học máy.
• Nhiều tên mà hồi quy tuyến tính được biết đến.
• Các thuật toán biểu diễn và học tập được sử dụng để tạo ra một mô hình hồi quy tuyến tính.
• Cách chuẩn bị tốt nhất cho dữ liệu của bạn khi lập mô hình bằng hồi quy tuyến tính.

Bạn không cần biết bất kỳ thống kê hoặc đại số tuyến tính nào để hiểu được hồi quy tuyến tính. Đây là phần giới thiệu nhẹ nhàng ở cấp độ cao về kỹ thuật này nhằm cung cấp cho bạn đủ kiến thức nền tảng để có thể sử dụng nó một cách hiệu quả vào các vấn đề của riêng bạn.

Hồi quy tuyến tính có phải là dựa phương pháp thống kê hay không ?

Trước khi chúng tôi đi sâu vào chi tiết của hồi quy tuyến tính, bạn có thể tự hỏi mình tại sao chúng tôi lại xem xét thuật toán này.

Nó không phải là một phương pháp từ thống kê?

Máy học, cụ thể hơn là lĩnh vực mô hình dự đoán chủ yếu liên quan đến việc giảm thiểu sai số của mô hình hoặc đưa ra dự đoán chính xác nhất có thể, với chi phí là khả năng giải thích. Trong học máy ứng dụng, chúng tôi sẽ mượn, sử dụng lại và đánh cắp các thuật toán từ nhiều lĩnh vực khác nhau, bao gồm cả thống kê và sử dụng chúng cho những mục đích này.

Do đó, hồi quy tuyến tính được phát triển trong lĩnh vực thống kê và được nghiên cứu như một mô hình để hiểu mối quan hệ giữa các biến số đầu vào và đầu ra, nhưng đã được học máy sử dụng. Nó vừa là một thuật toán thống kê vừa là một thuật toán học máy.

Tiếp theo, hãy xem lại một số tên thông dụng được sử dụng để chỉ mô hình hồi quy tuyến tính.

Hồi quy tuyến tính có nhiều tên.

Khi bạn bắt đầu xem xét hồi quy tuyến tính, mọi thứ có thể trở nên rất khó hiểu.

Lý do là vì hồi quy tuyến tính đã có từ rất lâu (hơn 200 năm). Nó đã được nghiên cứu từ mọi góc độ có thể và thường mỗi góc độ có một tên mới và khác nhau.

Hồi quy tuyến tính là một mô hình tuyến tính, ví dụ: một mô hình giả định mối quan hệ tuyến tính giữa các biến đầu vào (x) và biến đầu ra duy nhất (y). Cụ thể hơn, y có thể được tính toán từ sự kết hợp tuyến tính của các biến đầu vào (x).

Khi có một biến đầu vào duy nhất (x), phương pháp này được gọi là hồi quy tuyến tính đơn giản. Khi có nhiều biến đầu vào, tài liệu từ thống kê thường đề cập đến phương pháp là hồi quy tuyến tính nhiều lần.

Các kỹ thuật khác nhau có thể được sử dụng để chuẩn bị hoặc huấn luyện phương trình hồi quy tuyến tính từ dữ liệu, phương trình phổ biến nhất được gọi là Bình phương nhỏ nhất thông thường. Do đó, người ta thường đề cập đến một mô hình được chuẩn bị theo cách này là Hồi quy tuyến tính bình phương nhỏ nhất thông thường hoặc chỉ hồi quy bình phương nhỏ nhất.

Bây giờ chúng ta đã biết một số tên được sử dụng để mô tả hồi quy tuyến tính, chúng ta hãy xem xét kỹ hơn biểu diễn được sử dụng.

Biểu diễn mô hình hồi quy tuyến tính

Hồi quy tuyến tính là một mô hình hấp dẫn vì biểu diễn rất đơn giản.

Biểu diễn là một phương trình tuyến tính kết hợp một tập giá trị đầu vào cụ thể (x), nghiệm là đầu ra dự đoán cho tập giá trị đầu vào đó (y). Như vậy, cả giá trị đầu vào (x) và giá trị đầu ra đều là số.

Phương trình tuyến tính chỉ định một hệ số tỷ lệ cho mỗi giá trị hoặc cột đầu vào, được gọi là hệ số và được biểu thị bằng chữ cái Hy Lạp viết hoa Beta (B). Một hệ số bổ sung cũng được thêm vào, tạo cho đường thẳng một mức độ tự do bổ sung (ví dụ: di chuyển lên và xuống trên biểu đồ hai chiều) và thường được gọi là hệ số chặn hoặc hệ số chệch.

Ví dụ, trong một bài toán hồi quy đơn giản (một x và một y duy nhất), dạng của mô hình sẽ là:

y = B0 + B1 * x

Trong các kích thước cao hơn khi chúng ta có nhiều hơn một đầu vào (x), đường được gọi là mặt phẳng hoặc siêu mặt phẳng. Do đó, biểu diễn là dạng của phương trình và các giá trị cụ thể được sử dụng cho các hệ số (ví dụ B0 và B1 trong ví dụ trên).

Người ta thường nói về độ phức tạp của mô hình hồi quy giống như hồi quy tuyến tính. Điều này đề cập đến số lượng các hệ số được sử dụng trong mô hình.

Khi một hệ số trở thành 0, nó sẽ loại bỏ hiệu quả ảnh hưởng của biến đầu vào lên mô hình và do đó khỏi dự đoán được thực hiện từ mô hình (0 * x = 0). Điều này trở nên phù hợp nếu bạn xem xét các phương pháp chính quy thay đổi thuật toán học để giảm độ phức tạp của các mô hình hồi quy bằng cách gây áp lực lên kích thước tuyệt đối của các hệ số, đưa một số về không.

Bây giờ chúng ta đã hiểu về cách biểu diễn được sử dụng cho mô hình hồi quy tuyến tính, hãy xem xét một số cách mà chúng ta có thể tìm hiểu cách biểu diễn này từ dữ liệu.

Mô hình hồi quy tuyến tính máy học.

Học mô hình hồi quy tuyến tính có nghĩa là ước tính giá trị của các hệ số được sử dụng trong biểu diễn với dữ liệu mà chúng ta có sẵn.

Trong phần này, chúng ta sẽ xem xét ngắn gọn bốn kỹ thuật để chuẩn bị một mô hình hồi quy tuyến tính. Đây không phải là thông tin đủ để thực hiện chúng từ đầu, nhưng đủ để có được hương vị của việc tính toán và đánh đổi liên quan.

Còn nhiều kỹ thuật nữa vì mô hình đã được nghiên cứu rất kỹ. Hãy lưu ý đến Bình phương nhỏ nhất thông thường vì nó là phương pháp phổ biến nhất được sử dụng nói chung. Cũng lưu ý về Gradient Descent vì nó là kỹ thuật phổ biến nhất được dạy trong các lớp học máy.

1. Hồi quy tuyến tính đơn giản

Với hồi quy tuyến tính đơn giản khi chúng ta có một đầu vào duy nhất, chúng ta có thể sử dụng thống kê để ước tính các hệ số.

Điều này yêu cầu bạn tính toán các thuộc tính thống kê từ dữ liệu như phương tiện, độ lệch chuẩn, tương quan và hiệp phương sai. Tất cả dữ liệu phải có sẵn để duyệt và tính toán số liệu thống kê.

Đây là một bài tập thú vị trong excel, nhưng không thực sự hữu ích trong thực tế.

2. Bình phương nhỏ nhất thông thường

Khi chúng ta có nhiều hơn một đầu vào, chúng ta có thể sử dụng Bình phương Ít nhất Thông thường để ước tính giá trị của các hệ số.

Thủ tục Bình phương Ít nhất Thông thường tìm cách giảm thiểu tổng các phần dư bình phương. Điều này có nghĩa là với một đường hồi quy thông qua dữ liệu, chúng tôi tính toán khoảng cách từ mỗi điểm dữ liệu đến đường hồi quy, bình phương nó và tổng tất cả các lỗi bình phương lại với nhau. Đây là đại lượng mà bình phương nhỏ nhất thông thường tìm cách tối thiểu hóa.

Cách tiếp cận này coi dữ liệu như một ma trận và sử dụng các phép toán đại số tuyến tính để ước tính các giá trị tối ưu cho các hệ số. Nó có nghĩa là tất cả dữ liệu phải có sẵn và bạn phải có đủ bộ nhớ để chứa dữ liệu và thực hiện các phép toán ma trận.

Sẽ không bình thường nếu bạn tự thực hiện quy trình Bình phương nhỏ nhất thông thường trừ khi là một bài tập trong đại số tuyến tính. Có nhiều khả năng bạn sẽ gọi một thủ tục trong thư viện đại số tuyến tính. Thủ tục này rất nhanh để tính toán.

3. Gradient Descent

Khi có một hoặc nhiều đầu vào, bạn có thể sử dụng quy trình tối ưu hóa giá trị của các hệ số bằng cách giảm thiểu lặp đi lặp lại lỗi của mô hình trên dữ liệu đào tạo của bạn.

Thao tác này được gọi là Gradient Descent và hoạt động bằng cách bắt đầu với các giá trị ngẫu nhiên cho mỗi hệ số. Tổng các sai số bình phương được tính cho từng cặp giá trị đầu vào và đầu ra. Tỷ lệ học tập được sử dụng như một hệ số tỷ lệ và các hệ số được cập nhật theo hướng giảm thiểu lỗi. Quá trình được lặp lại cho đến khi đạt được sai số tổng bình phương tối thiểu hoặc không thể cải thiện thêm được nữa.

Khi sử dụng phương pháp này, bạn phải chọn tham số tốc độ học (alpha) xác định kích thước của bước cải tiến cần thực hiện trên mỗi lần lặp lại của quy trình.

Gradient descent thường được dạy bằng cách sử dụng mô hình hồi quy tuyến tính vì nó tương đối dễ hiểu. Trong thực tế, nó rất hữu ích khi bạn có một tập dữ liệu rất lớn với số lượng hàng hoặc số cột có thể không vừa với bộ nhớ.

4. Quy định hóa

Có những phần mở rộng của việc đào tạo mô hình tuyến tính được gọi là các phương pháp chính quy hóa. Những điều này nhằm giảm thiểu tổng sai số bình phương của mô hình trên dữ liệu huấn luyện (sử dụng bình phương nhỏ nhất thông thường) mà còn để giảm độ phức tạp của mô hình (như số lượng hoặc kích thước tuyệt đối của tổng tất cả các hệ số trong mô hình) .

Hai ví dụ phổ biến về các thủ tục chính quy hóa cho hồi quy tuyến tính là:

• Hồi quy Lasso: trong đó Bình phương nhỏ nhất thông thường được sửa đổi để cũng giảm thiểu tổng tuyệt đối của các hệ số (được gọi là chính quy L1).
• Hồi quy Ridge: trong đó Bình phương nhỏ nhất thông thường được sửa đổi để cũng giảm thiểu tổng bình phương tuyệt đối của các hệ số (được gọi là chính quy L2).

Các phương pháp này có hiệu quả để sử dụng khi có sự đồng nhất trong các giá trị đầu vào của bạn và các bình phương nhỏ nhất thông thường sẽ quá phù hợp với dữ liệu đào tạo.

Bây giờ bạn đã biết một số kỹ thuật để tìm hiểu các hệ số trong mô hình hồi quy tuyến tính, hãy xem cách chúng ta có thể sử dụng mô hình để đưa ra dự đoán trên dữ liệu mới.

Dự đoán với hồi quy tuyến tính

Với biểu diễn là một phương trình tuyến tính, việc đưa ra dự đoán cũng đơn giản như việc giải phương trình cho một tập hợp đầu vào cụ thể.

Hãy làm cho điều này cụ thể với một ví dụ. Hãy tưởng tượng chúng ta đang dự đoán cân nặng (y) từ chiều cao (x). Biểu diễn mô hình hồi quy tuyến tính của chúng tôi cho vấn đề này sẽ là:

                                y = B0 + B1 * x1

                                or

                                weight =B0 +B1 * height

Trong đó B0 là hệ số thiên vị và B1 là hệ số cho cột chiều cao. Chúng tôi sử dụng một kỹ thuật học tập để tìm một tập hợp các giá trị hệ số tốt. Sau khi tìm thấy, chúng tôi có thể cắm các giá trị chiều cao khác nhau để dự đoán trọng lượng.

Ví dụ, cho phép sử dụng B0 = 0,1 và B1 = 0,5. Hãy cắm chúng vào và tính trọng lượng (tính bằng kilôgam) của một người có chiều cao 182 cm.

                                weight = 0.1 + 0.5 * 182

                                weight = 91.1

Bạn có thể thấy rằng phương trình trên có thể được vẽ dưới dạng một đường trong hai chiều. B0 là điểm xuất phát của chúng ta bất kể độ cao của chúng ta là bao nhiêu. Chúng ta có thể chạy qua một loạt các độ cao từ 100 đến 250 cm và cắm chúng vào phương trình và nhận các giá trị trọng lượng, tạo ra đường thẳng của chúng ta.

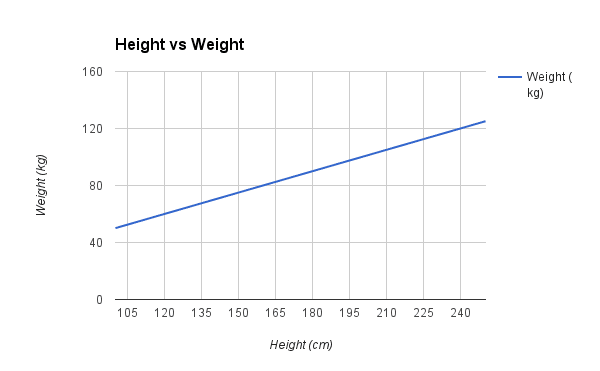
Bây giờ chúng ta đã biết cách đưa ra dự đoán dựa trên mô hình hồi quy tuyến tính đã học, hãy xem xét một số quy tắc cơ bản để chuẩn bị dữ liệu của chúng tôi để tận dụng tối đa loại mô hình này.

Chuẩn bị dữ liệu cho hồi quy tuyến tính

Hồi quy tuyến tính đã được nghiên cứu rất nhiều và có rất nhiều tài liệu về cách dữ liệu của bạn phải được cấu trúc để sử dụng tốt nhất mô hình.

Do đó, có rất nhiều sự ngụy biện khi nói về những yêu cầu và mong đợi này, điều này có thể gây khó chịu. Trong thực tế, bạn có thể sử dụng các quy tắc này nhiều hơn như các quy tắc ngón tay cái khi sử dụng Hồi quy bình phương nhỏ nhất thông thường, cách triển khai phổ biến nhất của hồi quy tuyến tính.

Hãy thử các cách chuẩn bị khác nhau cho dữ liệu của bạn bằng cách sử dụng các phép phỏng đoán này và xem cách nào phù hợp nhất với vấn đề của bạn.

• Giả định tuyến tính. Hồi quy tuyến tính giả định rằng mối quan hệ giữa đầu vào và đầu ra của bạn là tuyến tính. Nó không hỗ trợ bất cứ điều gì khác. Điều này có thể hiển nhiên, nhưng bạn nên nhớ khi có nhiều thuộc tính. Bạn có thể cần phải chuyển đổi dữ liệu để làm cho mối quan hệ trở nên tuyến tính (ví dụ: biến đổi nhật ký cho mối quan hệ hàm mũ).
• Loại bỏ tiếng ồn. Hồi quy tuyến tính giả định rằng các biến đầu vào và đầu ra của bạn không bị nhiễu. Cân nhắc sử dụng các hoạt động làm sạch dữ liệu cho phép bạn hiển thị và làm rõ tín hiệu trong dữ liệu của mình tốt hơn. Điều này quan trọng nhất đối với biến đầu ra và bạn muốn loại bỏ các giá trị ngoại lệ trong biến đầu ra (y) nếu có thể.
• Loại bỏ tính cộng gộp. Hồi quy tuyến tính sẽ quá khớp với dữ liệu của bạn khi bạn có các biến đầu vào tương quan cao. Cân nhắc tính toán các mối tương quan theo cặp cho dữ liệu đầu vào của bạn và loại bỏ các mối tương quan nhất.
• Phân phối Gaussian. Hồi quy tuyến tính sẽ đưa ra các dự đoán đáng tin cậy hơn nếu các biến đầu vào và đầu ra của bạn có phân phối Gaussian. Bạn có thể nhận được một số lợi ích bằng cách sử dụng các phép biến đổi (ví dụ: log hoặc BoxCox) trên các biến của bạn để làm cho phân phối của chúng trông giống Gaussian hơn.
• Thay đổi tỷ lệ đầu vào: Hồi quy tuyến tính thường sẽ đưa ra các dự đoán đáng tin cậy hơn nếu bạn thay đổi tỷ lệ các biến đầu vào bằng cách sử dụng chuẩn hóa hoặc chuẩn hóa.

Nguồn : https://machinelearningmastery.com/linear-regression-for-machine-learning