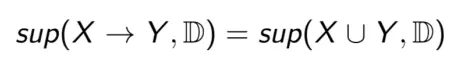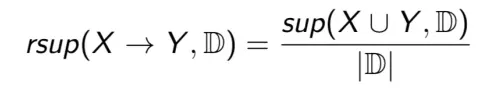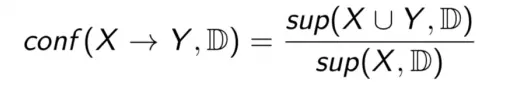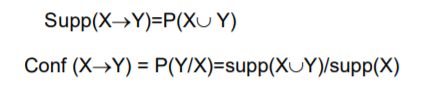Khai phá mẫu phổ biến và luật kết hợp
Bài đăng này đã không được cập nhật trong 5 năm
Câu chuyện "bia" và "bỉm"
Hẳn ai ban đầu cũng sẽ phải ngạc nhiên khi biết siêu thị Walmart bày trí những quầy bia và quầy bỉm cạnh nhau. Nghe chừng đây có vẻ là ý tưởng hết sức quái đản. Tuy nhiên chiến thuật này lại thực sự thành công và ảnh hưởng mạnh tới doanh số. Bạn hãy tưởng tượng một tình huống thú vị là một ông bố vào siêu thị mua đồ bỉm sữa cho con và rồi quay sang bên cạnh lại đụng món khoái khẩu và trường hợp ngược lại. WalMart tìm được quy luật này dựa trên nghiên cứu dữ liệu hành vi mua hàng của họ "Có 60% đàn ông đi siêu thị vào tối thứ 6, nếu họ mua bỉm cho trẻ em thì sẽ mua cả bia." Từ đó ta có thể nhận thấy rằng chúng ta hoàn toàn có thể tìm ra được mối quan hệ tương quan, kết hợp giữa các đối tượng để tạo ra giá trị cao hơn.
Các khái niệm và định nghĩa
1. Tập mục, Giao dịch và cơ sở dữ liệu giao dịch
Tập mục
Gọi I = {x1, x2, . . . , xn} là tập n mục (item). Một tập X ⊆ I được gọi là một tập mục (itemset).
Nếu X có k mục (tức |X| = k) thì X được gọi là k–itemset.
Ví dụ:
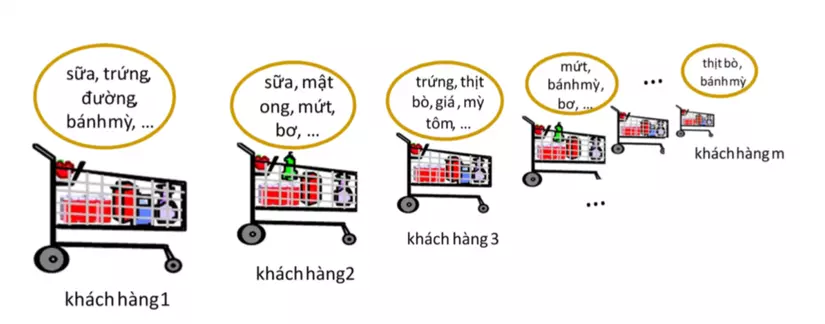
- Tập tất cả các mặt hàng thực phẩm trong siêu thị: I = {sữa, trứng, đường, bánh mỳ, mật ong, mứt, bơ, thịt bò, giá, . . . }.
- Tập tất cả các bộ phim: I = {pearl harbor, fast and furious 7, fifty shades of grey, spectre, . . . }.
Giao dịch
Ký hiệu D = {T1,T2, . . . , Tm} là cơ sở dữ liệu gồm m giao dịch (transaction). Mỗi giao dịch Ti ∈ D là một tập mục, tức Ti ⊆ I.
VD: Cơ sở giao dịch
Tập tất cả các mục I = {A, B, C, D, E}. Cơ sở dữ liệu giao dịch D = {T1, T2, T3, T4, T5, T6} trong đó:
- T1 = {A, B, D, E}
- T2 = {B, C, E}
- T3 = {A, B, D, E}
- T4 = {A, B, C, E}
- T5 = {A, B, C, D, E}
- T = {B, C, D}
Tập mục I là các sản phẩm trong siệu thị, Cơ sở giao dịch là những đơn mua của khách hàng.
- T1 = {sữa, trứng, đường, bánh mỳ}
- T2 = {sữa, mật ong, mứt, bơ}
- T3 = {trứng, mì tôm, thịt bò, giá}
2. Tập phổ biến, Luật kết hợp
Tập/mẫu phổ biến (frequent itemset/pattern)
Cho tập mục X (⊆ I)
-
Độ hỗ trợ của X, kí hiệu là sup(X, D), là số lượng giao dịch trong D chứa tập X:
sup(X, D) = |{T|T ⊆ D và X ⊆ T}| -
Độ hỗ trợ tương đối của X, kí hiệu là rsup(X, D) là số phần trăm các giao dịch trong D chứa X:
rsup(X, D) = sup(X, D)/|D| -
Tập mục X được gọi là tập phổ biến trong cơ sở giao dịch D nếu sup(X, D) >= minsup, với minsup là một ngưỡng độ hỗ trợ tối thiểu (minimum support threshold) do người dùng định nghĩa.
-
F là kí hiệu của tất cả các tập phổ biến
F(k) là kí hiệu của tập các tập phổ biến có độ dài k
VD: Các tập phổ biến (với minsup = 3) từ cơ sở dữ liệu D (tức số lần xuất hiện của tập trong 6 giao dịch >= 3) D = {T1, T2, T3, T4, T5, T6} trong đó:
-
T1 = {A, B, D, E}
-
T2 = {B, C, E}
-
T3 = {A, B, D, E}
-
T4 = {A, B, C, E}
-
T5 = {A, B, C, D, E}
-
T6 = {B, C, D}
Ta có tập các tập phổ biến là:
F = {A, B, C, D, E, AB, AD, AE, BC, BD, BE, CE, DE, ABD, ABE, ADE, BCE, BDE, ABDE }
- F(1) = {A, B, C, D, E}
- F(2) = {AB, AD, AE, BC, BD, BE, CE, DE}
- F(3) = {ABE, ABD, ADE, BCE, BDE}
- F(4) = {ABDE}
Luật kết hợp
Luật kết hợp là mối quan hệ giữa các tập thuộc tính trong cơ sở dữ liệu. Luật kết hợp là phương tiện hữu ích để khám phá các mối liên kết trong dữ liệu.
Một luật kết hợp là một mệnh đề kéo theo có dạng X -> Y, trong đó X, Y ⊆ I, thỏa mãn điều kiện X giao Y = rỗng. Các tập hợp X và Y được gọi là các tập hợp thuộc tính (itemset). Tập X gọi là nguyên nhân, tập Y gọi là hệ quả. Có 2 độ đo quan trọng đối với luật kết hợp: Độ hỗ trợ (support) và độ tin cậy (confidence), được định nghĩa như phần dưới đây.
-
Độ hỗ trợ
-
Độ hỗ trợ của một luật kết hợp X -> Y là tỷ lệ giữa số lượng các bản ghi chứa tập hợp X -> Y, so với tổng số các bản ghi trong D - Ký hiệu supp(X -> Y).
-
Độ hỗ trợ tương đối của luật X->Y trong cở sở dữ liệu D kí hiệu là rsup(X->Y, D) là số phần trăm các giao dịch trong D chứa cả X và Y.
-
Nếu độ hỗ trợ của một kết kết hợp X -> Y là 30% thì có nghĩa là 30% tổng số bản ghi chứa X hợp Y. Như vậy độ hỗ trợ mang ý nghĩa thống kê của luật.
-
Độ tin cậy
Độ tin cậy (confidence) của luật X → Y trong D, ký hiệu conf (X → Y , D), là tỉ lệ giữa số giao dịch chứa cả X và Y trên số giao dịch chỉ chứa X.
Ký hiệu độ tin cậy của một luật r là conf(r). Ta có 0 <= conf(r) <= 1
Độ hỗ trợ và độ tin cậy có xác xuất như sau:
- Độ hỗ trợ là xác xuất trong giao dịch chứa cả X và Y.
- Độ tin cậy là xác xuất có điều kiện mà một giao dịch trong D chứa Y trong khi đã chứa X (bản chất vẫn là mức độ in cậy của luật).
Kết luận
- Luật X -> Y được gọi là phổ biến nếu sup(X->Y, D) >= minsup (minsup do người dùng định nghĩa)
- Luật X-> Y được gọi là mạnh nếu độ tin cậy của nó lớn hơn hoặc bằng một ngưỡng minconf do người dùng định nghĩa: conf (X->Y) >= minconf
VD: Cơ sở giao dịch D = {T1, T2, T3, T4, T5, T6} trong đó:
- T1 = {A, B, D, E}
- T2 = {B, C, E}
- T3 = {A, B, D, E}
- T4 = {A, B, C, E}
- T5 = {A, B, C, D, E}
- T6 = {B, C, D}
Xét luật {B, C} -> {E} hay BC->E
- sup(BC->E, D) = sup(BCE, D) = 3 (số lần xuất hiện của bộ ba BCE trong các giao dịch thuộc D)
- conf(BC->E, D) = sup(BCE, D)/sup(BC, D) = 3/4 (=75%)
Xét luật {A, D} -> {B, E} hay AB->DE
-
Độ hỗ trợ sup(AD->BE, D) = sup(ABDE, D) = 3
-
Độ tin cậy conf(AD->BE, D) = sup(ABDE, D)/sup(AD, D) = 3/3 (=100%)
Tức ta có thể đưa ra kết luận là nếu trong giao dịch có chứa AD thì chắc chắn sẽ chứa BE
Tính chất
- Tính chất 1: Giả sử A,B ⊆ I là hai tập hợp với A⊆B thì sup(A) >= sup(B). Như vậy, những bản ghi nào chứa tập hợp B thì cũng chứa tập hợp A
- Tính chất 2: Giả sử A, B là hai tập hợp, A,B ⊆ I, nếu B là tập phổ biến và A⊆B thì A cũng là tập phổ biến. Vì nếu B là tập phổ biến thì sup(B) >= minsup, mọi tập hợp A là con của tập hợp B đều là tập phổ biến trong cơ sở dữ liệu D vì sup(A) >= sup(B) (Tính chất 1)
- Tính chất 3: Giả sử A, B là hai tập hợp, A ⊆ B và A là tập hợp không thường xuyên thì B cũng là tập hợp không thường xuyên (Tính chất 1) (Tức nếu A là tập hợp không phổ biến thì mọi tập cha của nó cũng không biến)
Các phương pháp khai phá
Khai phá luật kết hợp là việc phát hiện ra các luật kết hợp thỏa mãn các ngưỡng độ hỗ trợ (minsup) và ngưỡng độ tin cậy (minconf) cho trước. Bài toán khai phá luật kết hợp gồm hai pha:
- Pha 1: Khai phá tất cả các tập phổ biến (FI) trong CSDL D với ngưỡng độ hộ trợ tối thiểu minsup (thường có độ tính toán cao và chiếm phần lớn thời gian trong khai phá luật kết hợp)
- Pha 2: Sinh ra tất cả các luật mạnh từ các tập phổ biến khai phá được từ pha trước với ngưỡng tiến cậy tối thiểu mà minconf.
Thuật toán 1 – Thuật toán cơ bản:
Đầu vào: I, D, minsup, minconf
Đầu ra: Các luật kết hợp thỏa mãn ngưỡng độ hỗ trợ minsup , ngưỡng độ tin cậy minconf. Thuật toán:
- Tìm tất cả các tập hợp các tính chất có độ hỗ trợ >= minsup.
- Từ các tập hợp mới tìm ra, tạo ra các luật kết hợp có độ tin cậy >= minconf.
Thuật toán 2- Tìm luật kết hợp khi đã biết các tập hợp thường xuyên:
Đầu vào: I, D, minsup, minconf, tập phổ biến S
Đầu ra: Các luật kết hợp thỏa mãn ngưỡng độ hỗ trợ minsup, ngưỡng độ tin cậy minconf.
Thuật toán:
- Lấy ra một tập phổ biến s⊆S, và một tập con X ⊆ s.
- Xét luật kết hợp có dạng X → (sX), đánh giá độ tin cậy của nó xem có nhỏ hơn minconf hay không. Thực chất, tập hợp S mà ta xét đóng vai trò của tập hợp giao S = X hợp Y, và do X giao (S – X) = rỗng, nên coi như Y = S – X.
Các thuật toán xoay quanh khai phá luật kết hợp chủ yếu nêu ra các giải pháp để đẩy nhanh việc thực hiện Pha 1 là tìm tất cả các tập phổ biến.
Thuật toán Apiori
Thuật toán dựa trên hai tính chất của tập phổ biến là:
- Nếu tập A phổ biến thì mọi tập con B của A đều phổ biến
- Nếu tập con A không phổ biến thì mọi tập cha của A là B đều không phổ biến
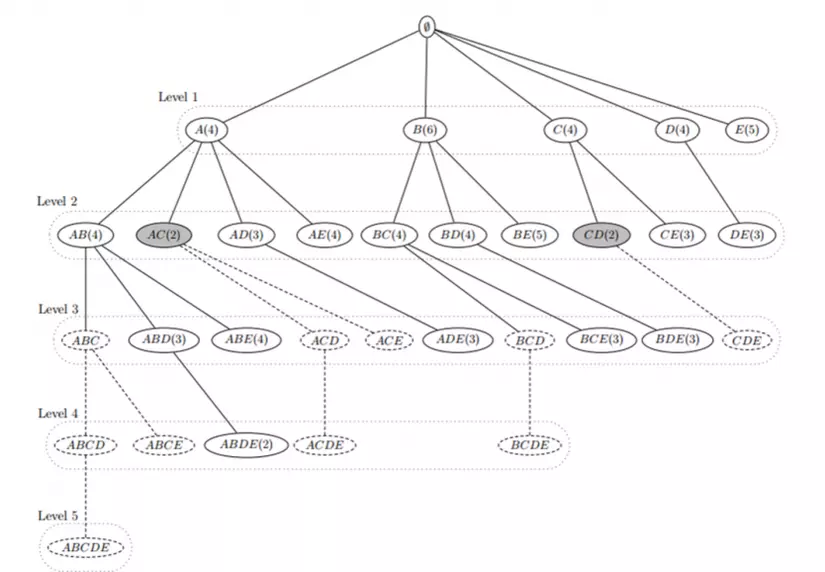
Các nút màu xam là các tập không phổ biến tức có sup < minsup
VD: Tập AC với sup(AC, D) = 2 (<minsup) thì các tập cha của AC là ACD, ACE, ACDE chắc chắn không phải là tập phổ biến -> bị loại ra khỏi cây và không cần tính độ hỗ trợ của chúng -> cây được cắt tỉa.
VD: Cơ sở giao dịch D, minsup=3, D = {T1, T2, T3, T4, T5, T6} trong đó:
- T1 = {A, B, D, E}
- T2 = {B, C, E}
- T3 = {A, B, D, E}
- T4 = {A, B, C, E}
- T5 = {A, B, C, D, E}
- T6 = {B, C, D}
Tập ứng viên C1
| 1-itemset | Độ hỗ trợ |
|---|---|
| A | 4 |
| B | 6 |
| C | 4 |
| D | 4 |
| E | 5 |
Tập phổ biến F1
| 1-itemset | Độ hỗ trợ |
|---|---|
| A | 4 |
| B | 6 |
| C | 4 |
| D | 4 |
| E | 5 |
Tập ứng viên C2 sinh từ tập ứng viên F1
| 2-itemset | Độ hỗ trợ |
|---|---|
| AB | 4 |
| AC | 2 |
| AD | 3 |
| AE | 4 |
| BC | 4 |
| BD | 4 |
| BE | 5 |
| CD | 2 |
| CE | 3 |
| DE | 3 |
Tập phổ biến F2
| 2-itemset | Độ hỗ trợ |
|---|---|
| AB | 4 |
| AD | 3 |
| AE | 4 |
| BC | 4 |
| BD | 4 |
| BE | 5 |
| CE | 3 |
| DE | 3 |
Tập ứng viên C3 sinh từ tập ứng viên F2: Không xét những tập chứa AC, CD
| 3-itemset | Độ hỗ trợ |
|---|---|
| ABD | 3 |
| ABE | 4 |
| ADE | 3 |
| BCE | 3 |
| BDE | 3 |
Tập phổ biến F3
| 3-itemset | Độ hỗ trợ |
|---|---|
| ABD | 3 |
| ABE | 4 |
| ADE | 3 |
| BCE | 3 |
| BDE | 3 |
Tập ứng viên C4 được sinh từ tập phổ biến F3
| 4-itemset | Độ hỗ trợ |
|---|---|
| ABDE | 3 |
Tập phổ biến F4
| 4-itemset | Độ hỗ trợ |
|---|---|
| ABDE | 3 |
Thuật toán Apriori
Đầu vào: cơ sở giao dịch D và tập mục I, minsup (dòng 1)
- Bước 1: Xét tập các tập phổ biến F = [] (dòng 2)
- Bước 2: Tìm tất cả tập phổ biến F1 (dòng 3)
- Bước 3: Xét tất cả các tập ứng viên Ck được sinh ra từ tập phổ biến Fk-1 (dòng 4)
- Bước 4: Sinh tập ứng viên Ck từ tập phổ biến Fk-1 (dòng 5)
- Bước 5: Tính sup của các tập ứng viên trong C (dòng 6->10)
- Bước 6: Nếu sup của ứng viên >= minsup thì ứng viên là một tập phổ biến được đưa vào tập phổ biến Fk (dòng 12)
- Thực hiện bước 4, 5, 6 cho đến khi không tìm được tập phổ biến
- Bước 7: Tập phổ biến bằng hợp của các tập phổ biến F1 -> Fk (dòng 15)
Hàm sinh các tập ứng viên từ tập phổ biến
Kiểm tra tập có chưa tập không phổ biến hay không
Sinh luật kết hợp phổ biến và mạnh từ tập phổ biến Đầu vào: Tập tất cả các tập phổ biến Đầu ra: Tập tất cả các luật phổ biến mạnh
- Bước 1: Khởi tạo tập luật mạnh R = [] (dòng 2)
- Bước 2: Xét từng tập phổ biến F (dòng 3)
- Bước 3: Tập X là tập các tập con của tập phổ biến F (X khác rỗng) (dòng 4)
- Bước 4: Trong khi X khác rỗng thực hiên vòng lặp (dòng 5)
- Bước 5: Y = phần tử lớn nhất trong X (dòng 6)
- Bước 6: Xét X = X \ Y (dòng 7)
- Bước 7: Nếu conf(Y ->F \ Y) >= minconf thì luật Y->F\Y là luật mạnh. Ngược lại xét X <- X {Z là tập con của Y} (dòng 8->12)
- Bước 8: Trả tập luật mạnh R (dòng 15)
Ưu và nhược điểm của phương pháp Apriori
Ưu điểm
- Dùng tính chất của tập phổ biến có thể cắt tỉa được nhiều nhánh, giảm bớt việc sinh các tập ứng viên từ những tập không hợp lệ (tập không phổ biến)
Nhược điểm
- Vẫn cần sinh một số lượng lớn các tập ứng viên. Cần quét cơ sở dữ liệu nhiều lần trong quá trình thực hiện thuật toán.
Trong bài tiếp theo chúng ta sẽ tìm hiểu những thuật khác như Brute-force, FP-Growth, ... và một số tiêu chí đánh giá khác ngoài độ hỗ trợ và độ tin cậy cũng như một số ứng dụng của khai phá luật kết hợp trong thực tế
All rights reserved