The Bias-Variance Decomposition
Bài đăng này đã không được cập nhật trong 5 năm
Như chúng ta đã biết, việc sử dụng maximum likelihood có thể dẫn đến over-fitting nếu model quá phức tạp lại được huấn luyện với dataset có lượng dữ liệu giới hạn( cái này có thể chứng minh toán học nhưng mình sẽ để 1 bài khác nhé  ). Tuy nhiên, nếu ta giảm số lượng tham số model để tránh over-fitting lại phải đối mặt với vấn đề model đơn giản quá sẽ không nắm bắt được các "trends" quan trọng hay thú vị của dữ liệu. Vậy thì làm thế nào để biết một model là đủ phức tạp? Hôm nay mình sẽ giới thiệu cho các bạn "a frequentist viewpoint" về vấn đề độ phức tạp model được biết đến với tên gọi rất thân thuộc:" bias-variance trade off". Trong bài viết mình chỉ giới hạn và lấy ví dụ bằng các mô hình tuyến tính cơ bản (linear basic models), tuy nhiên vấn đề được thảo luận của chúng ta vẫn có thể áp dụng rộng rãi và tổng quát hơn.
). Tuy nhiên, nếu ta giảm số lượng tham số model để tránh over-fitting lại phải đối mặt với vấn đề model đơn giản quá sẽ không nắm bắt được các "trends" quan trọng hay thú vị của dữ liệu. Vậy thì làm thế nào để biết một model là đủ phức tạp? Hôm nay mình sẽ giới thiệu cho các bạn "a frequentist viewpoint" về vấn đề độ phức tạp model được biết đến với tên gọi rất thân thuộc:" bias-variance trade off". Trong bài viết mình chỉ giới hạn và lấy ví dụ bằng các mô hình tuyến tính cơ bản (linear basic models), tuy nhiên vấn đề được thảo luận của chúng ta vẫn có thể áp dụng rộng rãi và tổng quát hơn.
Decision theory for regression problems
Trong "decision stage" bao gồm việc lựa chọn một hàm dự đoán của giá trị với đầu vào . Ta giả sử hàm loss là . Như vậy giá trị trung bình hay kỳ vọng của hàm loss được cho cho như sau:
Một lựa chọn phổ biến cho hàm loss trong các bài toán hồi quy (regression) đó là "squared loss" : . Trong trường hợp này, kỳ vọng của loss được viết lại thành:
Mục tiêu của chúng ta là chọn hàm sao cho nhỏ nhất. Như lẽ tự nhiên ta tính đạo hàm theo và giải phương trình đạo hàm bằng 0:
Đây chính là trung bình của xác suất điều kiện phụ thuộc hay còn được biết đến là "regression function" . Ta có thể hình dung như hình dưới đây.
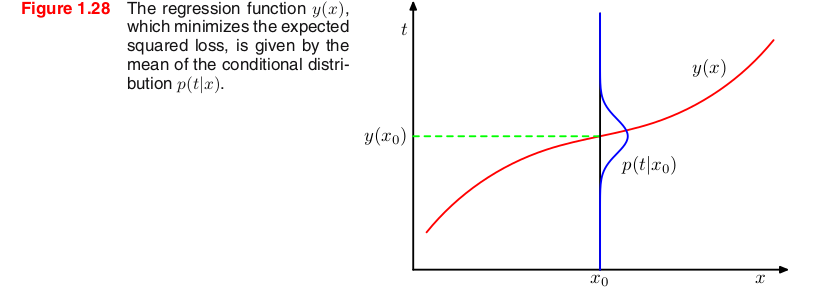
Ta sẽ phân tích kết quả vừa rồi theo một cách khác, cách này sẽ làm sáng tỏ một cách tự nhiên bài toán hồi quy. Vì đã biết rằng lời giải tối ưu chính là kỳ vọng của xác suất có điều kiện, do đó ta có thể viết lại thành phần bình phương như sau:
Ta vẫn giữ ký hiệu biểu thị . Thay thế vào hàm kỳ vọng của loss và biểu diễn tích phân trên ta nhận thấy thành phần tích ở giữa sẽ biến mất. Suy ra:
Ta nhận thấy rằng, khi cố gắng minimize hàm kỳ vọng của loss, ta sẽ tìm được hàm và thành phần thứ nhất sẽ biến mất. Tuy nhiên, thành phần thứ 2, là phương sai của phân bố và tính trung bình trên , nó đại diện cho sự thay đổi nội tại của target data và được coi là nhiễu. Thành phần thứ 2 này độc lập với hàm , do đó nó là thành phần không thể triệt tiêu của hàm loss. Điều này cũng ngụ ý rằng, bất kể cố gắng làm tốt thế nào khi xây dựng mô hình, luôn có những sai lệch chúng ta không thể kiểm soát được do dữ liệu luôn tồn tại những điểm nhiễu khó dự đoán trước.
The bias-variance decomposition
Trước hết mình nêu qua về định nghĩa bias và variance (thiên vị và phương sai):
- Bias là sự sai khác giữa trung bình dự đoán của mô hình chúng ta xây dựng với giá trị chính xác đang cố gắng để dự đoán. Một mô hình với trị số bias cao đồng nghĩa với việc mô hình đó không quan tâm nhiều tới dữ liệu huấn luyện, khiến cho mô hình trở nên đơn giản quá. Nó thường dẫn đến việc mô hình có mức độ lỗi cao cả trên tập huấn luyện và tập kiểm thử.
- Variance đặc trưng cho mức độ tản mát của giá trị dự đoán cho điểm dữ liệu. Mô hình với mức độ variance cao tập trung chú ý nhiều vào dữ liệu huấn luyện và không mang được tính tổng quát trên dữ liệu chưa gặp bao giờ. Từ đó dẫn đến mô hình đạt được kết quả cực kì tốt trên tập dữ liệu huấn luyện, tuy nhiên kết quả rất tệ với tập dữ liệu kiểm thử.
Ta lấy 1 ví dụ trực quan để các bạn hiểu rõ hơn:
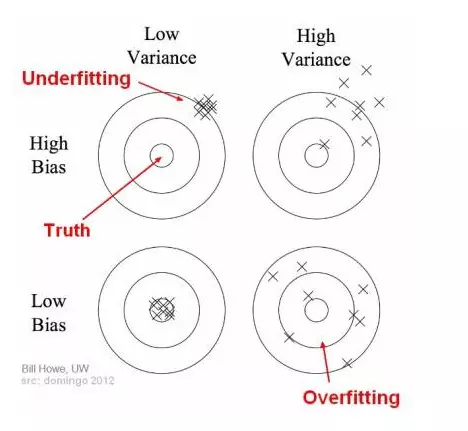
Trong hình trên, điểm trung tâm là điểm dự đoán tối ưu, cũng là giá trị chính xác mà chúng ta đang hướng tới.
Trong học có giám sát, underfitting xảy ra khi mô hình không thể mô tả được các mẫu cơ bản của dữ liệu. Các mô hình này thường có bias cao và variance thấp. Hiện tượng này dễ xảy ra khi lượng dữ liệu huấn luyện quá ít hoặc người phân tích dữ liệu cố gắng mô tả các dữ liệu phức tạp bằng các mô hình đơn giản như hồi quy tuyến tính hay hồi quy logistic.
Ngược lại, overfitting xảy ra khi mô hình biểu diễn cả dữ liệu nhiễu bên cạnh dữ liệu biểu diễn quy luật (có thể coi là dữ liệu sạch). Nó xảy ra khi train mô hình với rất nhiều dữ liệu bị nhiễu. Mô hình bị quá phức tạp so với mức độ cần thiết, bị lệ thuộc nhiều vào dữ liệu huấn luyện, thường có bias nhỏ và variance lớn. Model phức tạp kiểu như decision tree thường dễ bị overfitting.
Như vậy ta muốn mô hình của chúng ta phức tạp vừa đủ để có thể low bias và low variance.
Ta đi chứng minh nhận định trên:
Ta đặt , thay vào (1) ta được:
Ta nhắc lại, thành phần thứ 2 độc lập với do đó thành phần thứ 2 cũng là giá trị nhỏ nhất có thể đạt được của hàm trung bình loss. Thành phần thứ nhất phụ thuộc vào cách chọn hàm nên chúng ta sẽ tìm kiếm lời giải cho để minimize thành phần này. Nếu lượng data không giới hạn (và tất nhiên các tài nguyên tính toán cũng không giới hạn) ta có thể dự đoán hàm với độ chính xác tùy ý, từ đó chọn được hàm một cách tối ưu. Tuy nhiên, trong thực thế ta chỉ có 1 dataset với số lượng các điểm dữ liệu giới hạn, hệ quả là ta không thể tìm được hàm chính xác.
Giả sử, ta có một lượng lớn các tập dataset, mà mỗi dataset có N điểm dữ liệu, độc lập xác suất với nhau. Với mỗi dataset D ta chạy một thuật toán học và nhận được hàm dự đoán . Do các dataset khác nhau nên ta thu được các hàm khác nhau, và hệ quả là giá trị của hàm squared loss cũng khác nhau. Hiệu suất của một thuật toán học cụ thể sau đó được đánh giá bằng cách lấy giá trị trung bình trên toàn bộ tập hợp dữ liệu.
Như vậy, với mỗi dataset D thành phần đầu tiên của (2) được viết lại thành:
Vì đại lượng này sẽ phụ thuộc vào tập dữ liệu D cụ thể, chúng ta đi lấy giá trị trung bình của nó trên toàn bộ tập hợp dữ liệu. Ta thử biến đổi một chút biểu thức trên:
Bây giờ chúng ta lấy kỳ vọng của biểu thức này đối với D và lưu ý rằng thành phần cuối sẽ biến mất, suy ra:
Nếu xem là giá trị ta đang cố gắng dự đoán thì chuyện gì sẽ xảy ra nhỉ ? Vế phải của (4) chính là => Boom!!! (Các bạn đọc thử chứng minh công thức 4 nhé, khá thú vị ạ, mình mất gần tiếng mới chứng minh được công thức này :v) Thay vào (2), ta được:
Với
Như vậy để tối ưu được kỳ vọng loss ta thì model cần low bias và low variance. (điều cần chứng minh)
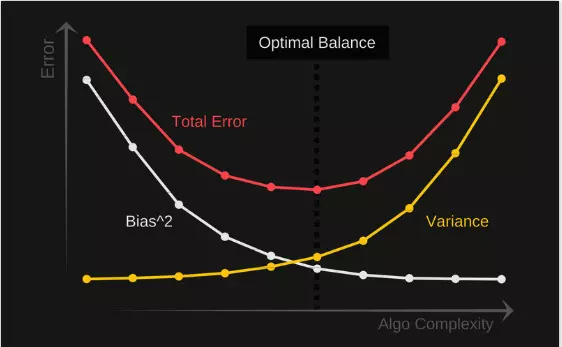
Điểm cân bằng của bias và variance sẽ không bao giờ bị overfitting hoặc underfitting. Do vậy, hiểu được mối quan hệ giữa 2 đại lượng là cực kì quan trong trong việc đánh giá được các mô hình dự đoán sau này.
Cảm ơn mọi người đã đón đọc.
Nguồn tham khảo: Machine learning and pattern recognition forum Machine learning co ban
All rights reserved