Hierarchical clustering - Phân cụm dữ liệu

Phân cụm là gì?

Phân cụm dữ liệu là bài toán gom nhóm các đối tượng dữ liệu vào thánh từng cụm (cluster) sao cho các đối tượng trong cùng một cụm có sự tương đồng theo một tiêu chí nào đó.

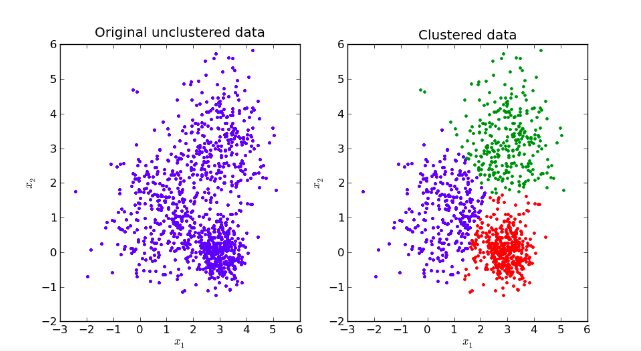
Đặc điểm

• Số cụm dữ liệu không được biết trước
• Có nhiều các tiếp cận, mối cách lại có vài kỹ thuật
• Các kỹ thuật khác nhau thường mang lại kết quả khác nhau.

Các độ đo khoảng cách

Tính chất của độ đo khoảng cách:

• Tính không âm (non-negative): d(x,y) >=0 và d(x, y) = 0 khai và chỉ khi x trùng y.
• Tính đối xứng (symmetic): d(x, y) = d(y, x)
• Tính tam giác (traingle inequality): d(x, y) + d(y, z) >= d(x, z)

Độ do Euclid chuẩn và độ đo Manhattan

• Cho hai điểm x = (x₁, x₂, ..., x_m) và y = (y₁, y₂, ..., y_m)
• Độ đo Euclid được xác định theo công thức

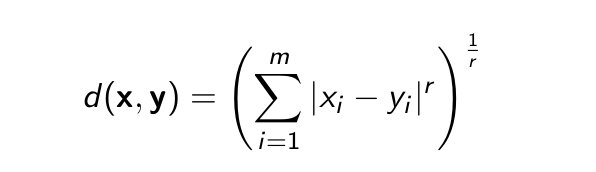
• Độ đo Euclid chuẩn (r = 2)

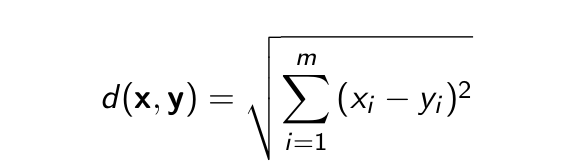
• Độ đo Manhattan

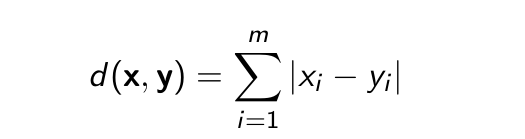
Độ đo Cosine

• Cho hai vecto x = (x₁, x₂, ..., x_m) và y = (y₁, y₂, ..., y_m)

• Độ đo Cosine được tính như sau

• Trong không gian dương:

  • Thoả mãn cả 3 tính chất
  • Giá trị nằm trong khoảng [0, 1]

Độ đo Hamming

• Được sử dụng khi các vecto ở dạng logic (true/false, 0/1)
• Khoảng cách giữa hai vecto được xác định là số chiều mà ở đó các giá trị tương ứng của hai vecto là khác nhau.
• Thỏa mãn cả 3 tính chất
• VD: v₁(0, 1, 0, 1, 0) và v₂ (1, 1, 0, 1, 0) vậy d(v₁, v₂) = 1

Độ đo Jaccard

• x, y là hai tập hợp
• Chỉ số Jaccard

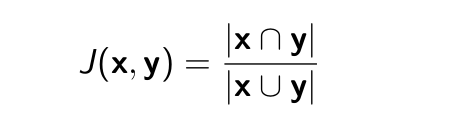
• Độ đo Jaccard

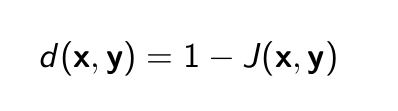
• Thỏa mãn cả 3 tính chất

Độ đo Kullback-Leibler (KL)

• Cho x = (x₁, x₂, ..., x_m) và y = (y₁, y₂, ..., y_m) là hai phân phối xác xuất rời rạc.
• Độ đo KL được tính như sau:

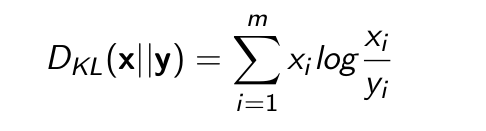
Trong đó không xét những vị trí có x_i = 0 hoặc y_i = 0.

• KL không thoải mãn tính chất đối xứng, tức DKL(x||y) có thể khác DKL(y||x)
• Đó đó, có thể tính độ đo dựa trên KL như sau:

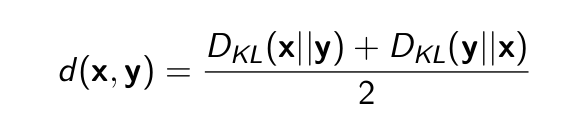
Hierarchical clustering (Phân cụm phân cấp)

Ý tưởng

Ban đầu mỗi điểm (đối tượng) là một cụm riêng biệt. Thuật toán phân cụm phân cấp sẽ tạo ra các cụm lớn hơn bằng các sát nhập các cụm nhỏ hơn gần nhau nhất tại mỗi vòng lặp.

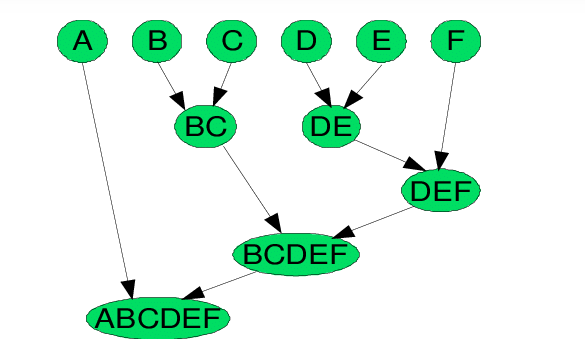
Thuật toán

Trước khi thực hiện bài toán cần phải xác định:

• Tiêu chí chọn hai cum "gần nhau nhất"
• Điều kiện dừng của thuật toán.
  
  

WHILE ( ! điều kiện dừng ) DO

• Chọn hai cụm gần nhau nhất theo tiêu chí đã xác định ban đầu.
• Sát nhập hai cụm gần nhau thành cụm lớn hơn.

END WHILE;

Các tiêu chí chọn hai cụm để sát nhập

• Centroid-linkage: Sát nhập hai cụm có khoảng cách giữa hai tâm của hai cụm này là nhỏ nhất.

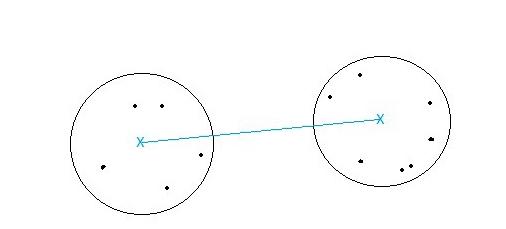
• Single-linkage: khoảng cách giữa hai điểm gần nhau nhất thuộc hai cụm. Sát nhập hai cụm có khoảng cách này nhỏ nhất.

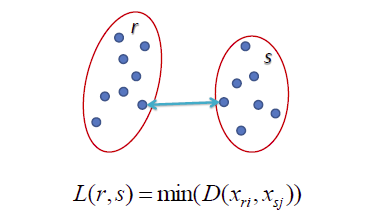
• Average-linkage: trung bình các khoảng cách giữa hai cặp điểm bất kì thuộc hai cụm. Sát nhập hai cụm có khoảng cách này nhỏ nhất.

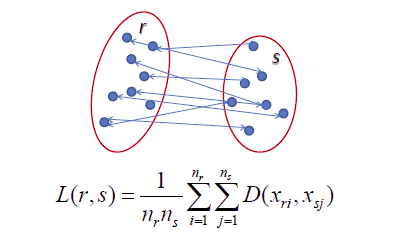
• Complete-linkage: khoảng cách giữa hai điểm xa nhau nhất của hai cụm, sát nhập hai cụm có khoảng cách này là nhỏ nhất.

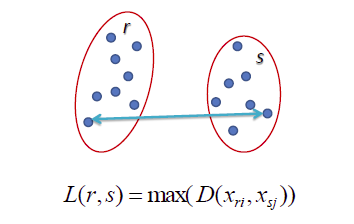
• Radius: bán kính của một cụm là khoảng cách từ tâm tới điểm xa nhất của cụm, sát nhập hai cụm nếu hai cụm tạo ra một cụm có bán kính nhỏ nhất.
• Diameter: đường kính của một cụm là khoảng cách của hai điểm xa nhau nhất trong cụm, sát nhập hai cụm nếu chúng tạo nên một cụm có đường kính nhỏ nhất.

Điều kiện dừng

• Có sự hiểu biết và phỏng đoán được số cụm trong tập dữ liệu.

• Khi việc sát nhập hai cụm tạo ra một cụm kém chất lượng.

• Khi tạo ra cụm cuối cùng chứa tất cả các đối tượng. Kết quả sẽ cho ra một cây phân cấp cụm (dendrogram). Có ý nghĩa trong một số trường hợp như xem xét cây tiến hóa của loài.

  

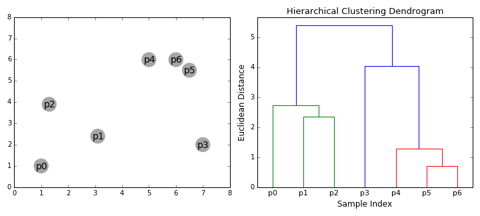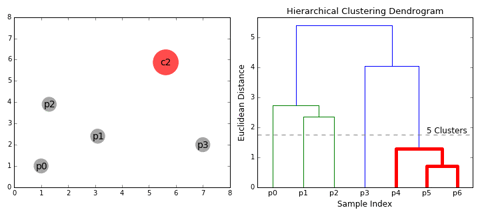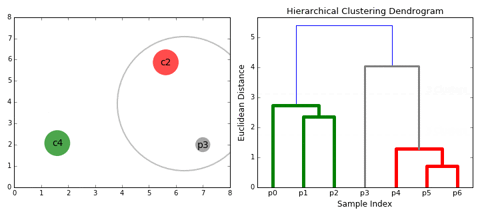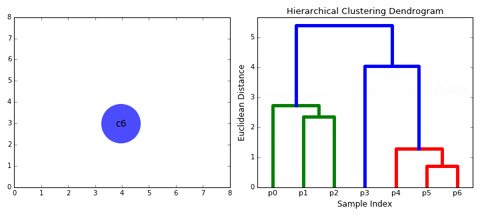
Phân loại

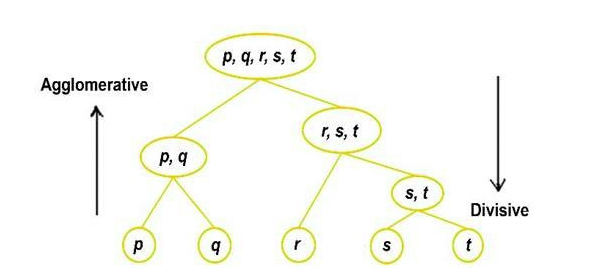
• Agglomerative hierarchical clustering: xuất phát mỗi điểm là một cụm, việc phân cụm là thực hiện sát nhập các cụm nhỏ thành cụm to hơn (bottom–up).
• Divisive hierarchical clustering: tất cả các đối tượng/điểm là một cụm, việc phân cụm là thực hiện chia tách cụm lớn thành các cụm nhỏ hơn (top–down).

Phân cụm phân cấp trong không gian khác Euclid

• Không tính toán dựa trên tọa độ các điểm (đối tượng)
• Áp dụng các độ đo khác Euclid như:
  • Jaccard
  • Kullback-Leibler
  • ...
• Không sử dụng được tâm của các cụm để tính toán như trong không gian Euclid. Thay vào đó chọn một đối tượng trong cụm làm trung tâm của cụm (clustroid). Đối tượng được chọn thường gần với tất cả các đối tượng trong cụm. Một số cách chọn:
  • Tổng khoảng cách từ clustroid đến các đối tượng khác trong cụm là nhỏ nhất.
  • Khoảng cách từ clustroid đến điểm xa nhất trong cụm là nhỏ nhất.
  • Trung bình khoảng cách từ clustroid đến các đối tượng khác trong cụm là nhỏ nhất.

Kết luận

• Ưu điểm của phân cụm phân lớp là không phải xác định trước số lượng cụm điều này khá vượt trội so với K-Means. Tuy nhiên, nó không hoạt động tốt với lượng dữ liệu khổng lồ.
• Thuật toán phân cụm phân lớp có thể được sử dụng để xác định, dự đoán số cụm trước khi thực hiện thuật toán K-Means.