Ứng dụng thuật toán Harris Corner Detector trong bài toán nối ảnh (Phần I)

Bài đăng này đã không được cập nhật trong 4 năm

Introduction

Xin chào mọi người, như mọi người đã biết trong các bài toán xử lý ảnh thì những đặc trưng của ảnh hay còn gọi là image features là vô cùng quan trọng trong việc giải quyết các bài toán thực tế như object detection, object classification, object localization, vân vân và vân vân. Hôm nay mình xin giới thiệu đến các bạn một thuật toán điển hình và mạnh mẽ trong việc tìm ra các corners cũng như các image features nhằm phục vụ cho các bài toán như image matching, image stitching for panorama,...

Giới thiệu qua về Harris Corner Detector(HCD), thì đây là thuật toán lần đầu tiên được giới thiệu bởi Chris Harris and Mike Stephens vào năm 1988. Ý tưởng chính của Harris là ông dựa vào sự biến đổi cường độ sáng tại một vùng lân cận được phát biểu như sau: một vùng nhỏ xung quanh các đặc trưng sẽ có 1 sự thay đổi lớn về cường độ sáng nếu một window dịch chuyển 1 đoạn (u,v) từ điểm (x,y) theo bất kì hướng nào.

Một ví dụ về ứng dụng HCD:

Mathematical overview

Chúng ta có công thức tính lượng thay đổi cường độ sáng khi dịch chuyển 1 đoạn [u, v] như sau:

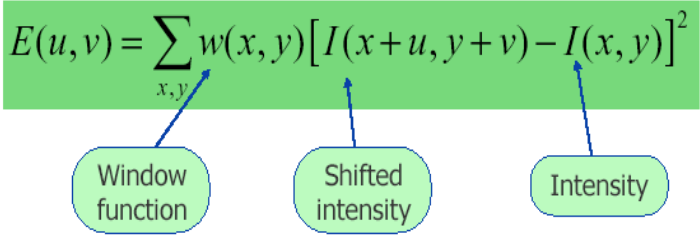
Trong đó:

W: Cửa sổ w có thể coi = 1 để cho đơn giản trong việc tính toán nhưng để chuẩn xác hơn cho kết quả đầu ra ta có thể coi đây như một mặt nạ Gauss(3x3, 5x5, ...)

I(x, y): Cường độ sáng tại điểm x, y

I(x + u, y + v): Cường độ sáng sau khi dịch chuyển cửa sổ đến điểm (x + u, y + v)

Ở đây ta sẽ áp dụng biến đổi Taylor để rút gọn lại biểu thức, ta có:

f(x + u, y + v) ≈ f(x, y) + ufx(x, y) + vfy(x, y)

Suy ra

Đến đây ta coi

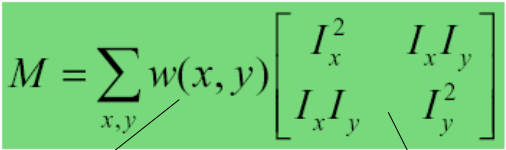
Như vậy cuối cùng ta có sự thay đổi cường độ sáng:

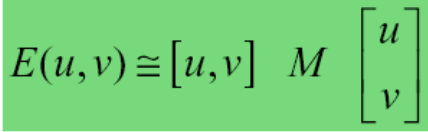
Việc phân loại và tìm ra các điểm ảnh có phải là các corner hay không dựa vào việc tính giá trị R (Mesure of corner response). Công thức R như sau:

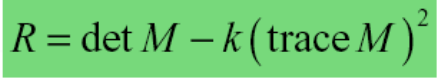
Trong đó: det(M) = AB - C^2 = λ1λ2, trace(M) = λ1 + λ2, λ1, λ2 là các giá trị bản địa of M tương ứng với độ cong của hàm địa phương quyết định xem điểm này có phải là corners hay không.

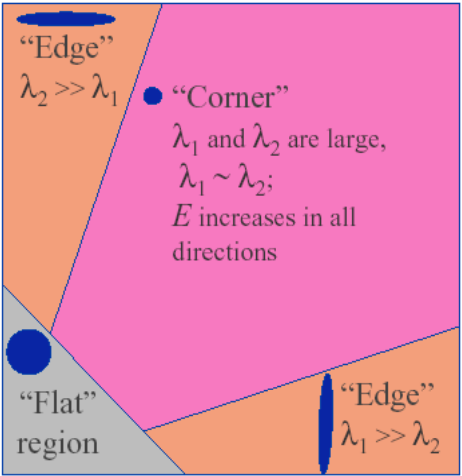
Intuitive Way to Understand Harris

Đạo hàm 1 chiều 1 tập các điểm (dx, dy) ta thu được:

Ở đây ta có thể nhận ra được sự khác nhau giữa các image features theo các hướng đạo hàm bậc 1 và đạo hàm bậc 2.

Plot các điểm nay lên trục đồ thị:

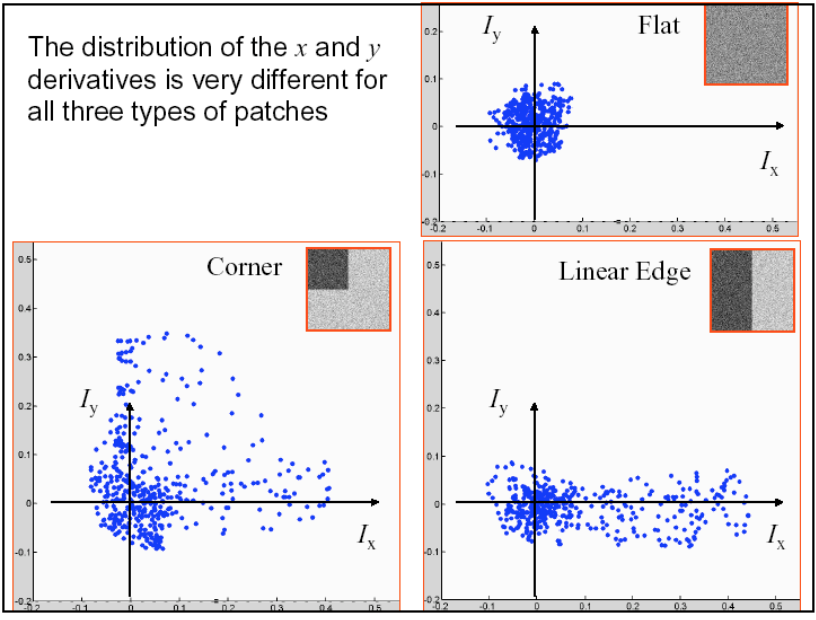
Chúng ta có thể thấy sự phân bố đạo hàm theo x, y là rất khác nhau giữa mặt phẳng, cạnh và góc trong một ảnh.

Step by step to implement Harris Algorithm

Chúng ta có thể sử dụng function cornerHarris trong thư viện OpenCv, nhưng để hiểu bản chất thuật toán hơn chúng ta sẽ implement lại từ đầu thuật toán.

Đầu tiên, chuyển từ ảnh RGB thành ảnh xám sau đó xoá nhiễu bằng mặt nạ Gauss
Thực hiện đạo hàm ảnh theo x, y bằng Sobel, Ix, Iy
Tính toán độ tương quan giữa các đạo hàm:
- A = Ix^2
- B = Ix * Iy
- C = Iy^2
Có 1 điểm đặc biệt ở đây là khi nhân ma trận, chúng ta sẽ không thực hiện phép nhân ma trận thông thường mà nhân các điểm tương ứng của ma trận này với ma trận kia: Ví dụ: A[i][j] = Ix[i][j] * Ix[i][j], sau đó áp dụng mặt nạ Gauss lên các ma trận A, B, C thu được _A, _B, _C
Tính corner response:

R = det(M) - k * Trace(M)

Với: det(M) = _A*_B - _C^2, Trace(M) = _A + _B, k là giá trị thực nghiệm [0,04 - 0,06]
Threshhold và lấy giá trị max ở mỗi vùng. Ở bước này sau khi threshhold, chúng ta sẽ lấy 1 cửa sổ (3x3) trượt qua từng pixel của R và lấy giá trị max ở mỗi vùng.

Code Implement

Bây giờ mình sẽ giới thiệu qua về code:

Import các thư viện cần thiết:

import cv2
import numpy as np
import matplotlib.pyplot as plt
from random import randint

// Hàm tìm giá trị max trong một cửa sổ 3x3 với tâm là [i, j] 

def find_max(R, i, j):
 max_point = 0
 
 for k in [-1, 0, 1]:
     for l in [-1, 0, 1]:
         if (max_point < R[i+k][j+l]):
             max_point = R[i+k][j+l]
 return max_point

\\ Hàm nhân 2 ma trận các điểm tương ứng

def matrix_multiply(I_x, I_y):
 (h, w) = I_x.shape
 result = np.empty((h, w))
 
 for i in range(0, h):
     for j in range(0, w):
         result[i][j] = I_x[i][j] * I_y[i][j]

 return result

\\ Hàm này sẽ giữ lại các vị trí có giá trị = giá trị max tại mỗi cửa sổ, các giá trị không thoả mãn sẽ bị đưa về 0

def nonmax_suppression(R, i, j, max_point):
 for k in [-1, 0, 1]:
     for l in [-1, 0, 1]:
         if (R[i+k][j+l] == max_point):
             continue
         else:
             R[i+k][j+l] = 0

\\ hàm tính trace của ma trận M

def calculate_trace(A, B):
 return A + B

\\ Hàm tính det của ma trận M

def calculate_det(A, B, C):
 det = matrix_multiply(A, B) - matrix_multiply(C, C)
 
 return det

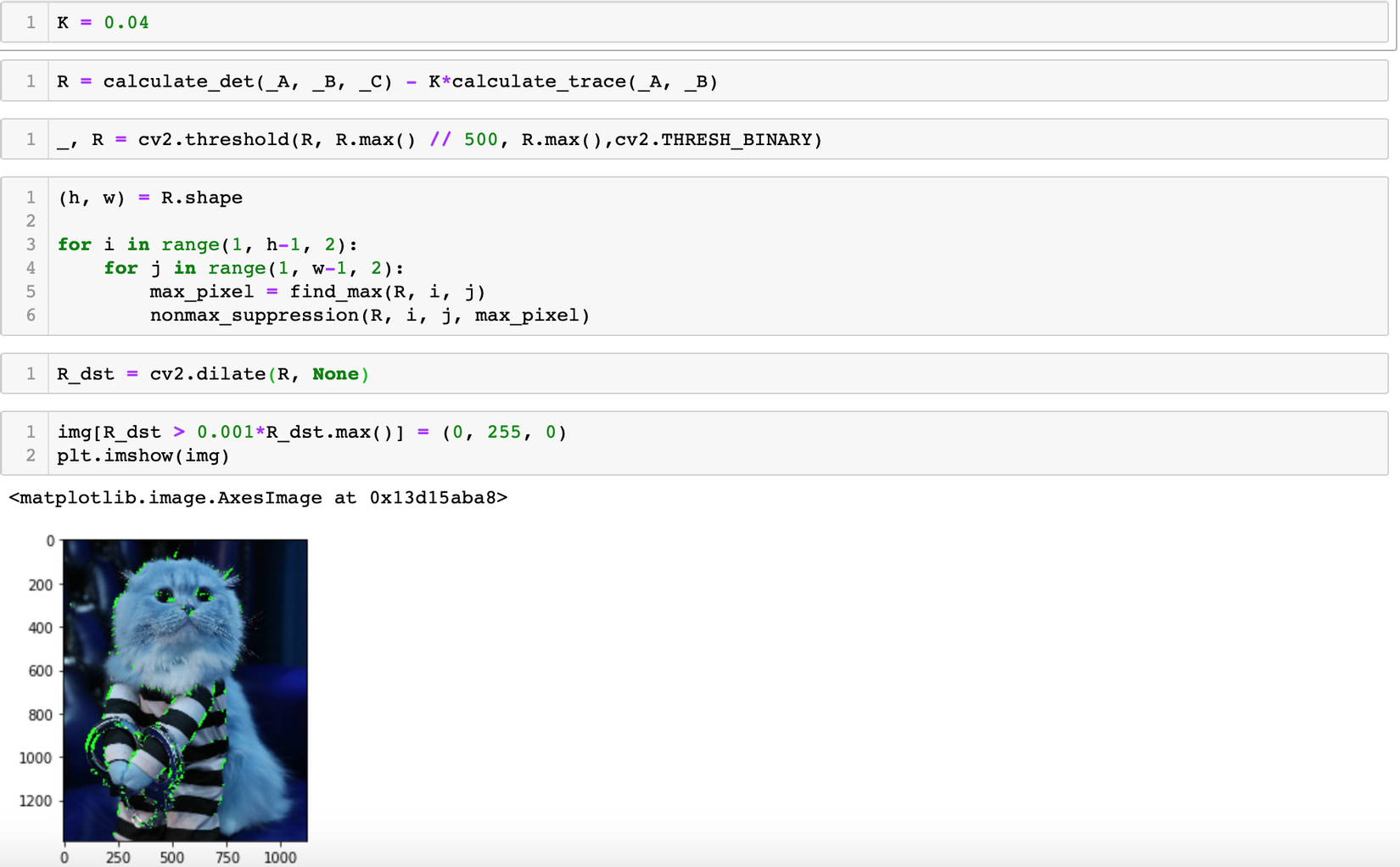
Chúng ta có thể thấy kết quả trả về là khá chính xác, có 1 lưu ý là ở bước chọn threshhold là khá quan trọng để có được kết quả tối ưu nhất.

Ở bài tiếp theo, mình sẽ giới thiệu về việc tận dụng thuật toán Harris trong ứng dụng nối ảnh để thu được kết quả như này. Cảm ơn mọi người đã đọc bài nha.