Support Vector Machine

Tổng quan

Support Vector Machine (SVM) là một trong những thuật toán mạnh mẽ cũng như được sử dụng phổ biến nhất trong Machine Learning. Ý tưởng chủ đạo của SVM là xây dựng một bộ phân lớp nhằm tối đa khoảng cách tối thiểu từ mỗi lớp tới siêu phằng phân chia. Để hiểu được cách xây dựng bài toán tối ưu cho SVM, chúng ta sẽ cần tới một chút kiến thức về hình học mà ở đây là khoảng cách từ một điểm tới một siêu phẳng, một chút kiến thức về tối ưu lồi, hàm đối ngẫu Lagrange và cách giải bài toán tối ưu có điều kiện ràng buộc tuyến tính. Trong bài viết này, tôi sẽ giới thiệu về thuật toán SVM để phân lớp một bộ dữ liệu là linearly separable ( có thể phân định tuyến tính được ) và để cho đơn giản chúng ta sẽ xem xét nó là một bài toán phân loại nhị phân.

I. Nhắc lại về Logistic Regression:

Có thể nhiều bạn sẽ đạt câu hỏi là: Tại sao lại là Logistic Regression mà không phải một thuật toán phân lớp nào khác ? Thì tôi xin được trả lời là vì ý tưởng của thuật toán này có nhiều điểm chung với SVM. Nhắc lại cho các bạn nào đã quên thì Logistic Regression xây dựng một phân bố xác suất cho mỗi lớp. Giả sử có một tập dữ liệu $S=\{x^{(i)}, y^{(i)}\}, i=1...m$ trong đó $x^{(i)} \in \real^{n+1}, x^{(i)}_0 =1$ và $y^{(i)} \in \{0,1\}$ ta sẽ có:

$$p(y^{(i)}=1|x^{(i)},\theta) = \sigma(\theta^Tx^{(i)})$$

$$\sigma(z) = \frac{1}{1 + e^{-z}} \in (0,1)$$

là xác suất để điểm dũ liệu thứ $i$ rơi vào class $1$ , $\theta \in \real^{n+1}$ được gọi là tham số của mô hình còn $\sigma$ biểu thi cho hàm sigmoid. Từ đây ta có thể dễ dàng suy ra được ngay.

$$p(y^{(i)}=0|x^{(i)},\theta) = 1 - p(y^{(i)}=1|x^{(i)},\theta)$$

Để quyết định điểm dữ liệu này rơi vào class nào ta chỉ cần đơn giản chọn ra class mà nó thuộc vào có xác suất lớn hơn. Nói đơn giản hơn, nếu ta chọn threshold = 0.5 thì một điểm dữ liệu sẽ rơi vào class $1$ khi:

$$p(y^{(i)}=1|x^{(i)},\theta) \ge 0.5$$

Ngược lại nó sẽ rơi vào class $0$. Ở đây nếu các bạn để ý một chút, thì sẽ thấy ngay biểu thức xác suất trên xảy ra khi và chỉ khi điều kiện dưới đây được thỏa mãn.

$$\theta^Tx^{(i)} \ge 0$$

$$\Leftrightarrow \theta_{0} \times x_{0}^{(i)} + \theta_{1} \times x_{1}^{(i)} + ... + \theta_{n} \times x_{n}^{(i)} \ge 0$$

Biểu thức trên nói cho ta biết rằng, nếu một điểm dữ liệu nằm về phía dương của siêu phẳng ( Hyper plane ) được định nghĩa bởi bộ tham số $\theta$ sẽ được nhận class $1$ và ngược lại sẽ nhận class $0$. Nói cách khác, Logistic Regression tìm kiếm một siêu phẳng phân cách sao cho, các điểm thuộc class $1$ sẽ nằm về phía dương của nó, còn các điểm thuộc class $0$ sẽ nằm về phía âm.

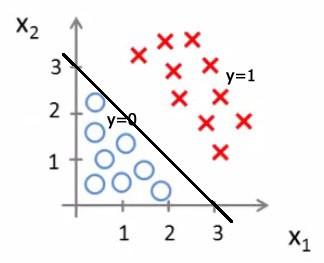
Figure 1: Decision Boundary được sinh ra từ Logistic Regression.

Một quan sát quan trọng nữa là nếu định lượng $\theta^Tx^{(i)}$ càng lớn ( một cách hình học mà nói tức là điểm dữ liệu $x^{(i)}$ nằm càng xa về phía dương của hyper plane ) thì xác suất để điểm dữ liệu đó rới vào class $1$ sẽ càng lớn và ngược lại. Điều này dẫn đến một kết luận rằng, nếu một điểm thuộc class $1$ thì ta sẽ muốn chúng cách siêu phẳng về phía dương càng xa càng tốt, tương tự một điểm thuộc class $0$ sẽ cần cách về phía âm càng xa càng tốt.

Tương đương với việc chúng ta đang cần tìm một đường phân tách sao cho các điểm thuộc cùng một lớp sẽ nằm về cùng một phía tương ứng và khoảng cách từ điểm gần nhất của mỗi lớp tới đường phân tách đó là lớn nhất có thể. Đó chính là tư tưởng của Support Vector Machine.

II. Khoảng cách từ một điểm tới một siêu phẳng:

Nhắc lại một chút về kiến thức hình học, nếu các bạn đã quên thì khoảng cách từ một điểm đến một mặt phẳng được định nghĩa như sau. Giả sử mặt phẳng (P) có phương trình: $ax + by + cz + d = 0$ và một điểm $A(x_0,y_0,z_0)$ thì khoảng cách từ điểm A tới mặt phẳng (P) sẽ là:

$$d(A,(P)) = \frac{|a \times x_0 + b \times y_0 + c \times z_0 + d|}{\sqrt{a^2 + b^2 + c^2}}$$

Tổng quát công thức trên lên không gian có số chiều lớn, ta suy được một công thức tương tự:

$$d(\bold{x},P) = \frac{|\theta_0 \times x_0 + \theta_1 \times x_1 + ... + \theta_n \times x_n|}{\sqrt{ \theta_1^2 + ... + \theta_n^2} } = \frac{|\theta^T\bold{x}|}{\sqrt{ \theta_1^2 + ... + \theta_n^2}}$$

trong đó $\bold{x},\theta \in \real^{n+1}, x_0 =1$ và $d(\bold{x},P)$ được gọi là khoảng cách từ điểm $\bold{x}$ tới siêu phẳng (hyper plane) $P$. Ở đây, nếu ta bỏ dấu trị tuyệt đối của tử số đi, ta sẽ xác định được điểm $\bold{x}$ nằm về phía nào của siêu phẳng, nếu tử số là dương, tức là điểm $\bold{x}$ nằm về phía dương của siêu phẳng, ngược lại thì nó sẽ nằm về phía âm.

Để thuận tiện khi thực hiện các phép toán trong SVM, tôi xin được phép sửa lại một chút về ký hiệu, việc sửa đổi này không gây ảnh hưỡng tới kết quả của các biểu thực đã nêu ở trên. Tiếp theo, thay vì dùng ký hiệu $\theta$ để biểu thị cho tham số của siêu phẳng, tôi sẽ đổi nó thành 2 vector khác là $\bold{w}$ và $b$ với $\bold{w} = [\theta_1, ....,\theta_n] \in \real^n$ và $b = \theta_0 \in \real$ và loại bỏ thành phần $x_0 =1$ ra khỏi vector $\bold{x}$. Biểu thức ở trên có thể viết lại dưới dạng sau đây.

$$d(\bold{x},P) = \frac{|b +w_1 \times x_1 + ... + w_n \times x_n |}{\sqrt{w_1^2 + w_1^2 + ... + w_n^2} } = \frac{|\bold{w}^T\bold{x} + b|}{\Vert\bold{w}\Vert_2}$$

III. Margin:

Xem xét một tập dữ liệu $S =\{ x^{(i)}, y^{(i)} \},i=1...m$ với $x^{(i)} \in \real^n$ và $y^{(i)} \in \{-1,1\}$ ( ở đây để thuận tiện cho các phép tính sau này, tôi xin phép đổi domain của $y$ từ $\{0,1\}$ về $\{-1, 1\}$ ) và một linear classifier được tham số hóa bởi 2 vector $\bold{w}$ và $b$ có dạng sau:

$$\hat{y} = h_{\bold{w},b}(x) = g(\bold{w}^Tx + b)$$

trong đó $g(\bold{w}^Tx + b) =1$ nếu $\bold{w}^Tx + b \ge 0$ và $-1$ nếu $\bold{w}^Tx + b < 0$. Ta xét khoảng cách từ một điểm trong tập dữ liệu tới siêu phẳng được định nghĩa bởi $\bold{w}$ và $b$.

$$\gamma^{(i)} = \frac{|\bold{w}^T\bold{x}^{(i)} + b|}{\Vert\bold{w}\Vert_2}$$

Từ các giả thiết trên, ta thấy có một quan sát quan trọng: một điểm sẽ được phân lớp đúng nếu.

$$\gamma^{(i)} = \frac{ y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b)}{\Vert\bold{w}\Vert_2} > 0$$

Như đã thảo luận ở phần trên, ta muốn các điểm dữ liệu cách đường phân cách xa càng tốt, cụ thể hơn, nếu một điểm thuộc lớp $1$ ta sẽ muốn $\bold{w}^T\bold{x}^{(i)} + b$ là một số dương càng lớn càng tốt, còn nếu thuộc lớp $-1$ ta sẽ cần $\bold{w}^T\bold{x}^{(i)} + b$ là một số âm càng nhỏ càng tốt. Điều này có thể được đảm bảo nếu điểm gần nhất của mỗi lớp, cách xa đường phân cách nhất có thể.

Margin của tập dữ liệu được định nghĩa là khoảng cách từ điểm gần nhất ( bất kỳ lớp nào ) trong tập dữ liệu đó tới siêu phẳng phân cách.

$$\gamma^* = \min_{i=1...m}{\gamma^{(i)}}$$

IV. Bài toán tối ưu Margin:

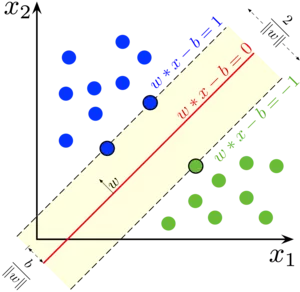
Figure 2: Biễu diên hình học của SVM. (Nguồn: Wikipedia)

Ta cần cực đại hóa margin của bộ dữ liệu, thỏa mãn điều kiện khoảng cách từ mọi điểm trong bộ dữ liệu tới siêu phẳng phân cách tối thiểu phải bằng margin này. Nói cách khác, bài toán tối ưu của chúng ta có dạng sau đây.

$$\max_{w,b} \gamma^*$$

$$s.t: \gamma^{(i)} \ge \gamma^{*}, i=1...m$$

Tuy nhiên, chúng ta sẽ không giải trực tiếp bài toán này vì nó rất phức tạp, thay vào đó chúng ta sẽ biến nó về dạng đơn giản hơn để có thể giải được. Trước hết, có một điều quan trọng nữa tôi muốn các bạn hiểu. Cùng xem xét lại công thức khoảng cách từ một điểm dữ liệu tới đường phân cách.

$$\gamma^{(i)} = \frac{ y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b)}{\Vert\bold{w}\Vert_2}$$

Nếu tôi thay $\bold{w} = k\bold{w}$ và $b = kb$ ( với $k$ là một số thực dương bất kỳ ) thì $\gamma^{(i)}$ không thay đổi. Ngoải ra việc nhân $\bold{w}$ và $b$ với một số nguyên dương $k$ bất kỳ không làm ảnh hưởng tới dự đoán của linear classifier ta xem xét ở trên i.e $g(\bold{w}^Tx + b) = g(k\bold{w}^Tx + kb)$. Sử dụng tính chất bất biến trên ta có thể giả sử các điểm gần nhất với siêu phẳng phân cách thỏa mãn.

$$y^{*} (\bold{w}^T\bold{x}^{*} + b) = 1$$

Như vậy, với mọi điểm trong bộ dữ liệu, ta sẽ cần điều kiện sau được đảm bảo:

$$y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b) \ge 1, i=1....m$$

Bài toán tối ưu của chúng ta có thể được viết lại dưới dạng sau:

$$\max_{w,b}{\frac{1}{\Vert\bold{w}\Vert_2}}$$

$$s.t: y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b) \ge 1, i=1....m$$

Hàm norm ở mẫu trông không hề đẹp tí nào phải không, vì vậy thay vì tối đa biểu thức kia ta sẽ chuyển về tối thiểu bình phương biểu thức nghịch đảo của nó, ngoài ra ta sẽ nhân thêm hệ số để nó đẹp hơn khi đạo hàm.

$$\min_{w,b}{\frac{1}{2} } {\Vert\bold{w}\Vert_2^2}$$

$$s.t: y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b) \ge 1, i=1....m$$

Bài toán tối ưu trên có hàm mục tiêu là một hàm convex ( tôi sẽ không giải thích ở đây, bạn nào muốn tìm hiểu thêm hãy vào phần trích dẫn bên dưới ) với điều kiện ràng buộc là tuyến tính. Ta có thể giải nó bằng quy hoạch toàn phương ( Quadratic Programming), tuy nhiên trong bài viết này, thay vì giải trực tiếp bài toán tối ưu trên, chúng ta sẽ đi giải bài toán đối ngẫu của nó, cũng vì bài toán đối ngẫu có những tính chất đẹp, mà trong đó có thể giúp chúng ta áp dụng được SVM hiệu quả với những bộ dữ liệu là non-linearly separable (không thể phân định tuyến tính).

Xem thêm:

• https://en.wikipedia.org/wiki/Convex_function
• https://machinelearningcoban.com/2017/03/12/convexity/

V. Lagrange duality:

Tạm thời bỏ qua SVM, tôi sẽ nói một chút về bài toán tối ưu có ràng buộc tổng quát và cách giải các bài toán dạng này sử dụng phương pháp nhân tử Lagrange. Phần này sẽ không đi sâu vào lý thuyết mà chúng ta sẽ chỉ cố gắng hiểu các concept quan trọng và các kết quả đã được chứng minh trước đó. Xem xét một bài toán tối ưu có dạng sau đây.

$$\min_{w} f(w)$$

$$s.t: g_i(w) \le 0, i=1..k$$

$$h_i(w) = 0, i=1,..l$$

Trong đó $w$ được gọi là biến tối ưu ( điều cực kỳ quan trọng khi làm việc với các bài toán tối ưu là bạn biết chúng ta cần tối ưu hàm mục tiêu theo biến nào), $f(w)$ được gọi là hàm mục tiêu, $g_i(w),i=1...k$ được gọi là tập các ràng buộc bất phương trình và $h_i(w),i=1...l$ là các ràng buộc phương trình. Ta định nghĩa Lagrangian của bài toán trên có dạng như sau.

$$\mathcal{L} (w,\alpha,\beta) = f(w) + \sum_{i=1}^{k}{\alpha_ig_i(w)} + \sum_{i=1}^{l}{\beta_ih_i(w)}$$

$$\alpha_i \ge 0, i=1...k$$

Trong đó $\alpha_i$ và $\beta_i$ được gọi là các nhân tử Lagrange. Ta xem xét định lượng sau:

$$\theta_p{(w)} = \sup_{\alpha,\beta: \alpha \ge 0} \mathcal{L} (w,\alpha,\beta)$$

$$= \sup_{\alpha,\beta: \alpha \ge 0}{ f(w) + \sum_{i=1}^{k}{\alpha_ig_i(w)} + \sum_{i=1}^{l}{\beta_ih_i(w)} }$$

Với $\sup$ tương ứng với hàm Supremum. Ta thấy một quan sát quan trọng sau, nếu $w$ có giá trị vi phạm các ràng buộc của bài toán ( $g_i(w) > 0$ hoặc $h_i(w) \ne 0$ ) thì giá trị $\sup_{\alpha,\beta: \alpha \ge 0} \mathcal{L} (w,\alpha,\beta) = \infty$, ngược lại nếu giá trị $w$ thỏa mãn các ràng buộc của bài toán thì $\sup_{\alpha,\beta: \alpha \ge 0} \mathcal{L} (w,\alpha,\beta) = f(w)$.

Có hơi khó hiểu phải không, để tôi giải thích thêm một chút nhé, giả sử $w =w_0$ là giá trị thỏa mãn càng ràng buộc ( $g_i(w_0) \le 0, i=1...k$ và $h_i(w_0) = 0,i=1..l)$, thì với mọi giá trị $\alpha_i \ge 0, \beta_i$ bất kỳ ta luôn có:

$$f(w_0) + \sum_{i=1}^{k}{\alpha_ig_i(w_0)} + \sum_{i=1}^{l}{\beta_ih_i(w_0)} \le f{(w_0)}$$

Lấy $\sup$ của biểu thức trên ta sẽ thu được giá trị $f(w_0)$. Ngược lại nếu giá trị $w = w_0$ vi phạm các ràng buộc, thì tồn tại giá trị $\alpha_i \ge 0, \beta_i$ sao cho.

$$f(w_0) + \sum_{i=1}^{k}{\alpha_ig_i(w_0)} + \sum_{i=1}^{l}{\beta_ih_i(w_0)} > f(w_0)$$

Lấy $\sup$ của biểu thức trên ta sẽ thu được giá trị $\infty$. Tiếp theo ta xem xét định lượng sau đây.

$$\inf_{w} \theta_p{(w)} = \inf_{w} \sup_{\alpha,\beta: \alpha \ge 0} \mathcal{L} (w,\alpha,\beta)$$

Với $\inf$ tương ứng với hàm Infimum. Biểu thức trên nói cho ta biết rằng, ta cần tìm giá trị cận dưới của hàm $\sup_{\alpha,\beta: \alpha \ge 0} \mathcal{L} (w,\alpha,\beta)$, tức là tại đó giá trị w mà thỏa mãn các ràng buộc của bài toán ban đầu và giá trị của $\mathcal{L} (w,\alpha,\beta)$ là nhỏ nhất tương ứng với giá trị của $f(w)$ là nhỏ nhất. Thêm nữa nếu lầy argument của hàm này sẽ cho ta nghiệm $w$ của bài toán ban đầu.

Ta định nghĩa bài toán đối ngẫu của bài toán trên như sau. Giả sử:

$$\theta_{D}(\alpha,\beta) = \inf_{w} \mathcal{L} {(w,\alpha,\beta)}$$

Khác với ở trên thay vì lấy $\sup$ theo 2 biến $\alpha,\beta$ thì ta lấy $\inf$ theo biến $w$. Biểu thúc này nói cho ta biêt rằng, ta cần chọn giá trị w sao cho tại đó giá trị của $\mathcal{L} {(w,\alpha,\beta)}$ là nhỏ nhất. Sau đó ta tiếp tục lấy $\sup$ theo 2 biến $\alpha,\beta$ của hàm trên.

$$\sup_{\alpha,\beta: \alpha \ge 0} {\theta_{D} = \sup_{\alpha,\beta:\alpha \ge 0} \inf_{w} \mathcal{L} {(w,\alpha,\beta)}}$$

Từ đây ta suy ra được rằng, ta cần chọn giá trị $\alpha, \beta: \alpha \ge 0$ sao cho $\inf_{w} \mathcal{L} {(w,\alpha,\beta)}$ là lớn nhất, nói cách khác chính là giá trị $\alpha, \beta$ sao cho $\mathcal{L} {(w,\alpha,\beta)} = f(w)$ ( giá trị tối đa cùa $\mathcal{L} {(w,\alpha,\beta)}$ mà tại đó w thỏa mãn các ràng buộc của đề bài ) hay chính là giá trị tối ưu của bài toán đầu tiên. Nếu lấy argument hàm trên, ta cũng thu được nghiệm $\alpha, \beta$ của bài toán đối ngẫu.

Theo bất đẳng thức Max-Min ta có:

$$\sup_{\alpha,\beta:\alpha \ge 0} \inf _{w} \mathcal{L}(w,\alpha,\beta) \le \inf_{w} \sup_{\alpha,\beta:\alpha \ge 0} \mathcal{L}(w, \alpha,\beta)$$

Giấu $"="$ xảy ra khi và chỉ khi đối ngẫu mạnh xảy ra ( Strong Duality).

Tiêu chuẩn Slater (Slater conditions): Nếu tồn tại một điểm strictly feasible (và bài toán gốc là lồi), thì strong duality xảy ra.

Nói cách khác, nếu hàm mục tiêu $f$ và ràng buộc $g$ là hàm lồi (convex), $h$ là tuyến tính và tồn tại một tập hợp các giá trị $w$ nào đó làm cho $g$ là strictly feasible ( thõa mãn chặt hay $g_i(w) <0,i=1..m$) thì đối ngẫu mạnh xảy ra. Khi đói ngẫu mạnh xảy ra, việc giải bài toán đối ngẫu sẽ cho chúng ta kết quả của bài toán ban đầu.

Tiêu chuẩn KKT (Karush-Kuhn-Tucker conditions) : Nếu đối ngẫu mạnh xảy ra, thì nghiệm của hệ bài toán ban dầu và đối ngẫu sẽ thỏa mãn tiêu chuẩn KKT

Với $w^{*}$ là nghiệm của bài toán tối ưu ban đầu và $\alpha^{*}, \beta^{*}$ là nghiệm của bài toán đối ngẫu thỏa mãn hệ điều kiện sau:

$$\frac{\partial{ \mathcal{L} {(w^*,\alpha^*,\beta^*)} }}{ \partial{w_i} } = 0, i=1...n$$

$$\frac{\partial{ \mathcal{L} {(w^*,\alpha^*,\beta^*)} }}{ \partial{\beta_i} } = 0, i=1...l$$

$$\alpha_i^*g_i(w^*) = 0, i=1..k$$

$$g_i(w^*) \le 0, i=1..k$$

$$\alpha_i^* \ge 0, i=1..k$$

Nếu tồn tại các giá trị $w^*,\alpha^*,\beta^*$ thỏa mãn hệ điều kiện KKT, thì đó cũng là nghiệm của bài toán ban đầu và bài toán đối ngẫu. Ngoài ra các bạn hãy chú ý tới điều kiện thứ 3 trong hệ điều kiện KKT, điều kiện này có tên là: KKT dual complementarity condition. Chúng ta sẽ thấy điều kiện này có tác dụng ra sao ở mục dưới.

VI. Giải bài toán tối ưu cho SVM:

Xem xét bài toán tối ưu Margin:

$$\min_{w,b}{\frac{1}{2} } {\Vert\bold{w}\Vert_2^2}$$

$$s.t: y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b) \ge 1, i=1....m$$

Dạng bài toán này chưa đúng với dạng mà chúng ta đã xem xét ở mục V ( phần ràng buộc ). Cho nên Chúng ta sẽ biến đổi nó lại một chút để trông nó quen thuộc hơn.

$$\min_{w,b}{\frac{1}{2} } {\Vert\bold{w}\Vert_2^2}$$

$$s.t: 1 - y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b) \le 0, i=1....m$$

Chúng ta có thể nhận thấy rằng $1 - y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b) \le 0$ chính là ràng buộc $g_i(w) \le 0$ của bài toán chúng ta đã làm. Một quan sát quan trọng ở đây là với các điểm gần nhất với mặt phân cách ( thỏa mãn $y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b) = 1$) thì $\alpha_i > 0$ (xem lại điều kiện 3 KKT). Mô ta bẳng hình học, các điểm nằm trên đường nét đứt dưới đây chính là các điểm tại đó $\alpha_i > 0$, người ta còn gọi chúng là các support vectors. Các bạn sẽ thấy ngay sau đây các support vector này đóng vai trò quan trọng trong việc tính $\bold{w}$ của siêu phẳng phân cách.

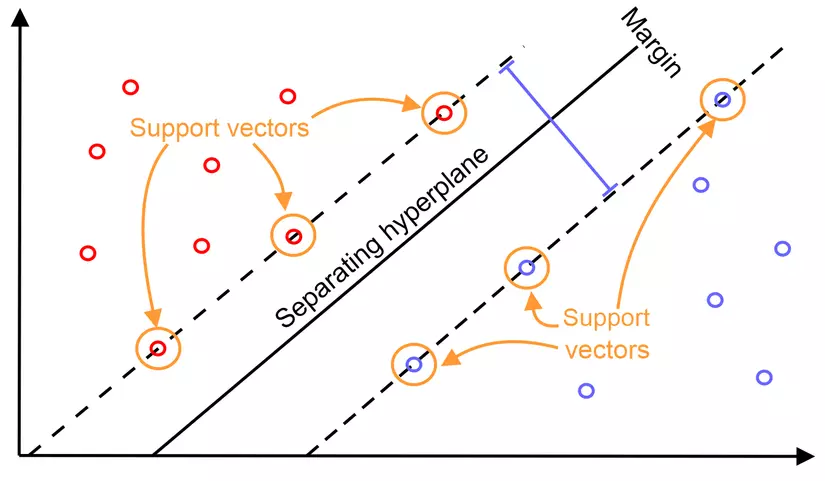
Figure 2: Các suport vectors của SVM. (Nguồn: Wikipedia)

Xét Largarian của bài toán tối ưu trên:

$$\mathcal{L} (\bold{w}, b, \alpha) = \frac{1}{2} {\Vert\bold{w}\Vert_2^2} - \sum_{i=1}^{m} \alpha_i [1 - y^{(i)} (\bold{w}^T\bold{x}^{(i)} + b) ]$$

Ở đây chúng ta chỉ có các $\alpha_i ,i=1..m$ vì chúng ta chỉ có ràng buộc bất phương trình mà không có ràng buộc phương trình. Chúng ta sẽ tối ưu $\bold{w}, b$ trong khi giữ cố định $\alpha$, để tạo ra $\theta_D$. Đạo hàm $\mathcal{L} (w,\alpha,\beta)$ theo biến $\bold{w}$ ta thu được.

$$\nabla_{\bold{w}} \mathcal{L} (\bold{w},b,\alpha) = \bold{w} - \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)}$$

Giải phương trình đạo hàm bằng 0, ta thu được.

$$\bold{w} = \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)}$$

Như đã thấy ở phần trên, hệ số $\alpha_i$ chỉ khác 0 đối với những điểm là support vectors, đối với những điểm không phải support vector, hệ số này sẽ bằng $0$ theo điều kiện 3 của tiêu chuẩn KKT. Nói cách khác, vector $\bold{w}$ của siêu phẳng phân cách chỉ phụ thuộc vào các support vectors có trong tập dữ liệu, và số lượng support vector này thường rất nhỏ so với kích thước của tập dữ liệu.

Xét đạo hàm $\mathcal{L} (w,\alpha,\beta)$ theo biến $b$ ta thu được.

$$\frac{\partial {\mathcal{L} (\bold{w},b,\alpha)} }{\partial b} = \sum_{i=1}^{m} \alpha_i y^{(i)} = 0$$

Thé ngược vào Largarian ban đầu ta thu được:

$$\mathcal{L} (\bold{w}, b, \alpha) = \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} y^{(i)} y^{(i)} \alpha_i \alpha_j (x^{(i)})^T x^{(j)}$$

Cuối cùng bài toán đối ngẫu với bài toán ban đầu sẽ có dạng sau đây:

$$\max_{\alpha} W(\alpha) = \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} y^{(i)} y^{(i)} \alpha_i \alpha_j (x^{(i)})^T x^{(j)}$$

$$s.t: \alpha_i \ge 0,1=1...m$$

$$\sum_{i=1}^{m} \alpha_i y^{(i)} = 0$$

Ở đây tôi sẽ không tiếp tục giải tiếp nữa, thay vào đó nếu bạn muốn đưa ra dự đoán cho một điểm dữ liệu mới, chúng ta chỉ cần xét dấu biểu thức $\bold{w}^Tx + b$, nếu $\bold{w}^Tx + b \ge 0$ thì $y=1$, ngược lại $y=-1$. Sử dụng các kết quả đã thu được ở trên, ta có:

$$\bold{w}^Tx + b = \bigg ( \sum_{i=1}^{m} \alpha_i y^{(i)} x^{(i)} \bigg) ^T x+ b$$

$$= \sum_{i=1}^{m} \alpha_i y^{(i)} (x^{(i)})^Tx + b$$

Trong đó hãy chú ý inner product của điểm dữ liệu mới với các điểm dữ liệu trong tập dữ liệu, đây là một phần quan trọng nếu sau này bạn muốn hiểu cách áp dụng Kernel Method với SVM, giúp chúng ta làm việc với các dữ liệu không thể phân định tuyến tính được. Ngoải ra nếu bộ dữ liệu là gần phân định tuyến tính, chúng ta sẽ phải thay đổi hàm mục tiêu một chút, các kỹ thuật này tôi sẽ giới thiệu trong các bài sau, cảm ơn các bạn đã theo dõi.

VII. Tham khảo:

• https://machinelearningcoban.com/2017/04/09/smv/#-xay-dung-bai-toan-toi-uu-cho-svm
• http://cs229.stanford.edu/notes/cs229-notes3.pdf
• https://www-cs.stanford.edu/people/davidknowles/lagrangian_duality.pdf
• https://en.wikipedia.org/wiki/Support_vector_machine
• https://machinelearningcoban.com/2017/04/02/duality/