Giới thiệu

Các mô hình Deep Learning hiện nay đang tạo ra các mô hình tốt nhất để giải quyết rất nhiều các lĩnh vực và bài toán phức tạp như là speech recognition, computer vision, machine translation, v.v.. Tuy nhiên, để có thể huấn luyện tốt được các mô hình Deep Learning là rất khó khăn vì các mô hình hiện tại có cấu trúc bao gồm rất nhiều layer, trong suốt quá trình đó,phân bố dữ liệu qua các layer bị biến đổi. Do vậy, để mô hình có thể học nó là rất khó khăn. Vì vậy, trong bài viết này, mình sẽ đưa ra tầm quan trọng của việc normalization và các phương pháp của nó để các bạn có thể sử dụng chúng phù hợp với bài toán của bạn.

Tại sao chúng ta cần normalization?

Normalization luôn là lĩnh vực nghiên cứu tích cực trong Deep Learning. Các phương pháp Normalization có thể giúp mô hình huấn luyện nhanh và kết quả tốt. Cùng nhau đi tìm hiểu một số lợi ích của nó nhé:

1. Chuẩn hóa dữ liệu mỗi feature sẽ giữ được sự đóng góp của mọi feature trong quá trình huấn luyện trong trường hợp giá trị một số features cao hơn nhiều so với các feature còn lại. Với cách làm này sẽ làm mô hình unbiased (đối với các feature có giá trị cao)

2. Làm giảm Internal Covariate Shift. Việc mô hình càng sâu sẽ có nhiều layer cùng với đó là có nhiều hàm kích hoạt, nó sẽ làm biến đổi đi phân phối của dữ liệu. Do đó chúng ta cần chuẩn hóa lại nó để có được sự đồng bộ phân phối của dữ liệu trong quá trình huấn luyện. Khái niệm về Internal Covariate Shift mình lấy từ paper này, để hiểu rõ hơn các bạn đọc paper đấy nhá.

      Theo tác giả, nó được định nghĩa như sau: "Chúng tôi định nghĩa Internal Covariate Shift là sự thay đổi phân phối của các hàm kích hoạt trong mô hình do sự thay đổi của các tham số mô hình trong quá trình huấn luyện."
   

3. Trong paper này, tác giả cho rằng Batch Normallization có thể làm bề mặt hàm loss trở nên mịn màng hơn (i.e. nó giới hạn độ lớn của gradients chặt chẽ hơn nhiều ). Đại khái là việc tối ưu hàm mục tiêu sẽ trở nên dễ dàng và nhanh chóng hơn.

4. Việc tối ưu sẽ trở nên nhanh hơn bởi vì normalization không cho phép việc bùng nổ (explode) weights và nó giới hạn chúng trong một vùng nhất định.

5. Một lợi ích nữa nằm ngoài mục đích của normalization là nó giúp mô hình Regularization(chỉ một ít, không đáng kể ).

Với những lợi ích nên, ta có thể biết được phần nào tầm quan trọng của việc normalization trong việc huấn luyện mô hình hiệu quả, nhưng việc áp dụng nó vào mô hình sao cho hiệu quả thì không dễ dàng như vậy. Cùng mình đi qua một số câu hỏi sau:

1. Nên sử dụng phương pháp normalization nào trong mô hình CNN, RNN,..?
2. Hiện tượng gì xảy ra khi bạn thay đổi batch size của dataset?
3. Phương pháp normalization nào tốt nhất trong việc đánh đổi giữa sự phức tạp và độ chính xác của mô hình ? ...

Để trả lời các câu hỏi đó, chúng ta sẽ tìm hiểu về các phương pháp normalization, chúng có ưu điểm và nhược điểm gì ? Nhưng trước đó mình sẽ nói vấn đề khá quan trọng đó là normalization dữ liệu đầu vào. Let's get it.

Tầm quan trọng của việc normalization dữ liệu đầu vào ?

Giả sử rằng , chúng ta có data 2D với feature x_1và feature x_2 đi vào một neural network. Feature x_1 có giá trị từ -200 đến 200, có giá trị chênh lệch lớn và feature còn lại x_2 có giá trị từ -10 đến 10 có giá trị chênh lệch nhỏ hơn.

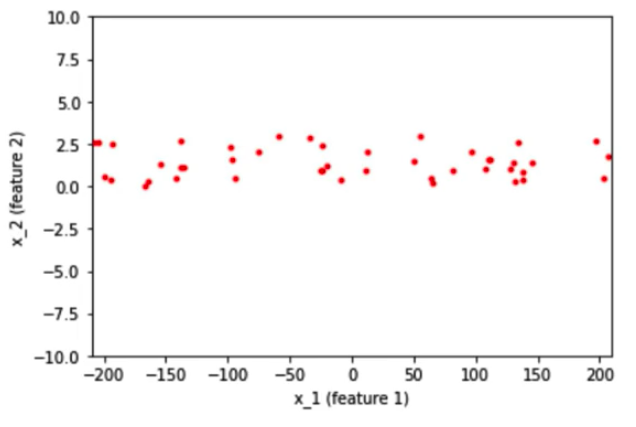
Sau khi normalied dữ liệu, khoảng dữ liệu khác nhau của 2 feature được đưa về cùng một khoảng từ -2 đến 2.

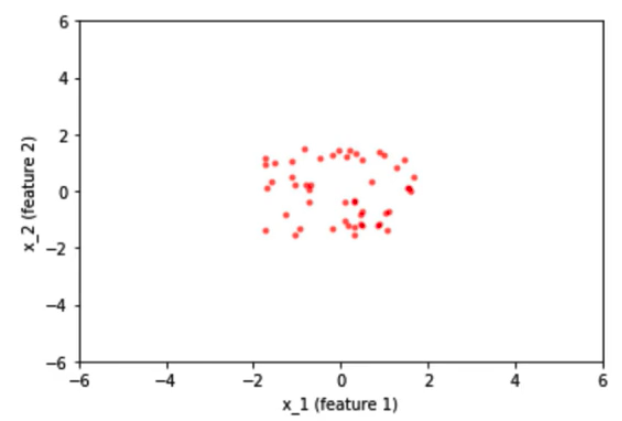
Bây giờ, mình sẽ cùng thảo luận tại sao normalization lại tốt trong trường hợp trên ?

Trước khi chúng ta normalized dữ liệu đầu vào, trọng số liên quan đến các features sẽ khác nhau rất nhiều vì giá trị đầu vào của các features biểu diễn ở các cùng khác nhau rất lớn từ -200 đến 200 và từ -10 đến 10. Để thích nghi với sự khác biệt giữa các features thì một số trọng số sẽ lớn và một số trọng số lại nhỏ. Nếu ta có trọng số lớn thì sẽ ảnh hưởng đến việc cập nhật nó trong quá trình lan truyền ngược cũng sẽ lớn và ngược lại. Vì sự phân bố không đồng đều của các trọng số nên dẫn tới việc thuật toán sẽ bị dao đồng trong vùng tối ưu trước khi nó tìm đến vị trí cực tiểu toàn cục.

Để tránh việc thuật toán học dành quá nhiều thời gian dao động khi tối ưu, ta normalize các features đầu vào về cùng tỉ lệ, phân phối. Từ đó thì dữ liệu đầu vào sẽ tỉ lệ và trọng số liên quan đến chúng cũng sẽ cùng tỉ lệ. Điều này giúp mô hình có thể học nhanh hơn.

Các phương pháp normalization

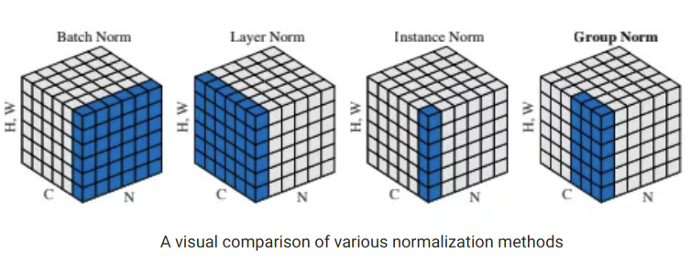
Normalization có nhiều phương pháp, như mình đã nói ở trên, việc lựa chọn phương pháp đúng cho mục đích của mô hình là rất quan trọng, sau đây mình sẽ đưa ra một số phương pháp mà mình tìm hiêu được :

Batch normalization

Batch normalization là một trong các phương thức normalization được sử dụng phổ biến trong mô hình deep learning. Nó cho phép đào tạo nhanh hơn và ổn dịnh các mạng nơ-ron sâu bằng cách ổn định sự phân bố của các đầu vào các layer trong quá trình huấn luyện. Cách tiếp cận này chủ yếu liên quan đến Internal Covariate Shift (ICS). Để cải thiện việc huấn luyện mô hình, điều quan trọng là phải giảm ICS bằng cách kiểm soát means và variances của dữ liệu đầu vào các layer, nôm na là điều chỉnh phân phối của dữ liệu cho đồng bộ trên toàn mô hình. Batch normalization là một phương thức chuẩn hóa các hàm kích hoạt trong mạng qua một mini-batch theo kích thước được định nghĩa trước đó. Với mỗi feature, batch normalization tính toán trung vị và phương sai của feature đó trong một mini-batch. Sau đó, nó trừ đi giá trị trung bình và chia cho độ lệch chuẩn của mini-batch đó. Công thức sẽ được biểu diễn như sau:

$$\mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i} / / mini-batch mean$$

$$\sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2} \quad / / mini-batch variance$$

Điều gì xảy ra nếu ta tăng cường độ trọng số làm cho mô hình trở nên tốt hơn. Để giải quyết vấn đề này, chúng ta có thể thêm γ và β để chúng có thể học scale và shift vs tham số tương ứng. Được mô tả như sau:

Input: Values of $x$ over a mini-batch: $\mathcal{B}=\left\{x_{1 \ldots m}\right\}$ Parameters to be learned: $\gamma, \beta$

Output: $\left\{y_{i}=\mathrm{BN}_{\gamma, \beta}\left(x_{i}\right)\right\}$

$$\mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i} / / mini-batch mean$$

$$\sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2} \quad / / mini-batch variance$$

$$\widehat{x}_{i} \leftarrow \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} / / normalize$$

$$y_{i} \leftarrow \gamma \widehat{x}_{i}+\beta \equiv \mathrm{B} \mathrm{N}_{\gamma, \beta}\left(x_{i}\right) / /scale and shift$$

Các vấn đề của batch normalization

1. Variable batch size -> Nếu barch size là 1, thì phương sai sẽ bằng 0, lúc này thì batch norm không hoạt động được. Hơn nữa, nếu ta cho mini-batch nhỏ thì nó sẽ thành nhiễu và ảnh hưởng đến quá trình huấn luyện mô hình.Cũng có vấn đề trong lúc huấn luyện. Như là, nếu bạn đang tính toán trên các máy khác nhau thì bạn phải có batch size giống nhau vì tham số γ và β sẽ khác nhau đối với các hệ thống khác nhau
2. Recurrent Neural Network -> Trong RNN, các kích hoạt lặp lại của mỗi bước thời gian sẽ có một câu chuyện khác nhau để kể (tức là số liệu thống kê). Điều này có nghĩa là chúng ta phải phù hợp với các layer batch norm riêng biệt cho mỗi time-step. Điều này làm cho mô hình phức tạp hơn và tốn không gian hơn vì nó buộc chúng ta phải lưu trữ số liệu thống kê cho từng bước thời gian trong quá trình đào tạo.

Các lợi ích của batch normalization

1. Làm giảm internal covariate shift (ICS) và tăng tốc độ huấn luyện cho mô hình deep learning.
2. Cách tiếp cận này làm giảm sự phụ thuộc của gradients vào tỉ lệ của các tham số hoặc giá trị ban đầu của chúng, dẫn đến learning rate cao hơn mà không có nguy cơ phân kỳ.
3. Batch normalization giúp bạn có thể sử dụng các chế độ phi tuyến bão hòa bằng cách ngăn mạng khỏi bị kẹt trong các chế độ bão hòa.

Weight normalization

Weight normalization là một quá trình đánh giá lại các trọng số vector trong một mạng neural sâu hoạt động bằng cách tách độ dài của các vectơ trọng lượng đó khỏi hướng của chúng. Nói một cách dễ hiểu, chúng ta có thể định nghĩa chuẩn hóa trọng số như một phương pháp để cải thiện tính tối ưu của các trọng số của mô hình mạng nơ-ron. Weight normalization đánh giá lại các trọng số như sau:

$$\boldsymbol{w}=\frac{g}{\|\boldsymbol{v}\|} \boldsymbol{v}$$

Việc tách các vector trọng số ra khỏi hướng của nó, điều này tương tự như cách hoạt động của batch normalization với phương sai. Điều khác biệt duy nhất ở đây là biến thể thay vì hướng. Về giá trị trung bình, các tác giả của bài báo này đã khéo léo kết hợp trung bình batch normalization và chuẩn hóa trọng lượng để có được giá trị mong muốn ngay cả trong các lô nhỏ nhỏ. Có nghĩa là chúng trừ đi giá trị trung bình của mini-batch nhưng không chia cho phương sai. Cuối cùng, họ sử dụng chuẩn hóa trọng số thay vì chia cho phương sai. Lưu ý: Trung bình ít nhiễu hơn so với phương sai (ở trên có nghĩa là một lựa chọn tốt so với phương sai) do quy luật số lớn. Bài báo chỉ ra rằng weight normalization kết hợp với batch normalization đạt được kết quả tốt nhất trên CIFAR-10.

Các lợi ích của weight normalization

1. Weight normalization cải thiện điều kiện của vấn đề tối ưu cũng như tăng tốc độ hội tụ sự giảm dần của SGD.
2. Nó có thể áp dụng tốt cho mô hình hồi quy như là LSTM cũng như là mô hình reinforcemnet learning,...

Layer normalization

Layer normalization là một phương thức để cải tiển tốc đố huấn luyện với các mô hình neural nerworks đa dạng. Không giống như batch normalization, phương pháp này ước tính trực tiếp số liệu thống kê chuẩn hóa từ các đầu vào tổng hợp đến các nơ-ron bên trong một lớp ẩn. Layer normalization về cơ bản được thiết kế để khắc phục những hạn chế của batch normalization như phụ thuộc vào các mini-batch, v.v. Layer normalization chuẩn hóa đầu vào trên các layers thay vì chuẩn hóa các features đầu vào trên từng batch trong batch normalization.

Một mini-batch bao gồm nhiều ví dụ với cùng một số tính năng. Mini-batch là ma trận (hoặc tenxơ) trong đó một trục tương ứng với lô và trục kia (hoặc các trục) tương ứng với các kích thước đặc trưng.

$$\mu_{i}=\frac{1}{m} \sum_{j=1}^{m} x_{i j}$$

$$\sigma_{i}^{2}=\frac{1}{m} \sum_{j=1}^{m}\left(x_{i j}-\mu_{i}\right)^{2}$$

$$\hat{x_{i j}}=\frac{x_{i j}-\mu_{i}}{\sqrt{\sigma_{i}^{2}+\epsilon}}$$

Trong các bài báo, các tác giả tuyên bố rằng layer normalization hoạt động tốt hơn batch normalization trong các bài toán RNN,..

Các lợi ích của layer normalization

1. Layer normalization có thể dễ dàng áp dụng cho mô hình RNN bởi vì nó tính toán thống kê chuẩn hóa riêng biệt trên từng time-step.
2. Cách tiếp cận này có hiệu quả trong việc ổn định các trạng thái ẩn trong các mạng hồi quy.

Instance normalization

Layer normalization và instance normalization rất tương tự nhau nhưng sự khác biệt giữa chúng là instance normalization chuẩn hóa qua mỗi channel trong mỗi ví dụ huấn luyện thay vì chuẩn hóa qua các features đầu vào trong một ví dụ huấn luyện. Không giống như batch normalization,lớp instance normalization được áp dụng trong quá trình thử nghiệm rất tốt ( do không phụ thuộc vào mini-batch ), được áp dụng cho toàn bộ loạt ảnh thay vì một ảnh duy nhất

$$y_{t i j k}=\frac{x_{t i j k}-\mu_{t i}}{\sqrt{\sigma_{t i}^{2}+\epsilon}}$$

$$\quad \mu_{t i}=\frac{1}{H W} \sum_{l=1}^{W} \sum_{m=1}^{H} x_{t i l m}$$

$$\quad\sigma_{t i}^{2}=\frac{1}{H W} \sum_{l=1}^{W} \sum_{m=1}^{H}\left(x_{t i l m}-m u_{t i}\right)^{2}$$

Trong đó, x∈ ℝ T ×C×W×H là đầu vào tensor chứa một batch của T ảnh. Gọi xₜᵢⱼₖ biểu thị phần tử tijk-th của nó, trong đó k và j mở rộng kích thước không gian (Chiều cao và Chiều rộng của hình ảnh), i là kênh đặc trưng (kênh màu nếu đầu vào là hình ảnh RGB) và t là chỉ số của hình ảnh trong lô.

Các lợi ích của instance normalization

1. Việc chuẩn hóa này đơn giản hóa quá trình huấn luyện của mô hình.
2. Instance normalization có thể áp dụng trong quá trình thử nghiệm mô hình.

Group normalization

Group normalization có thể nói là một giải pháp thay thế cho batch normalization. Cách tiếp cận này hoạt động bằng cách chia các kênh (channels) thành các nhóm và tính toán trong mỗi nhóm giá trị trung bình và phương sai để chuẩn hóa tức là chuẩn hóa các tính năng trong mỗi nhóm. Không giống như batch normalization, chuẩn hóa nhóm độc lập với kích thước batch size và độ chính xác của nó cũng ổn định trong nhiều loại batch size.

Chúng ta có thể thấy Group normalization đứng ở giữa instance normalization và layer normalization. Khi chúng ta cho tất cả các kênh (channels) vào 1 nhóm thì group normalization trở thành layer normalization. Còn khi cho mỗi keenh(channel) vào các nhóm khác nhau thì nó trở thành instance normalization

$$\mu_{i}=\frac{1}{m} \sum_{k \in \mathcal{S}_{i}} x_{k}, \quad \sigma_{i}=\sqrt{\frac{1}{m} \sum_{k \in \mathcal{S}_{i}}\left(x_{k}-\mu_{i}\right)^{2}+\epsilon}$$

$$\mathcal{S}_{i}=\left\{k \mid k_{N}=i_{N},\left\lfloor\frac{k_{C}}{C / G}\right\rfloor=\left\lfloor\frac{i_{C}}{C / G}\right\rfloor\right\}$$

$$\hat{x}_{i}=\frac{1}{\sigma_{i}}\left(x_{i}-\mu_{i}\right)$$

$$y_{i}=\gamma \hat{x}_{i}+\beta$$

Các lợi ích của group normalization

1. Nó có thể thay thể batch normalization trong một số bài toán về Deep Learning.
2. Dễ dàng triển khai nó.

Kết luận

Qua bài viết này các bạn đã thấy được tầm quan trọng của việc normalization. Trong các phương thức normalization trên thì Batch Normalization vẫn là phương thức tốt nhất và được áp dụng rộng rãi cho nhiều bài toán trong Deep Learning. Tuy nhiên, vào một ngày không đẹp trời nào đó, mô hình của bạn chạy lâu và khó hội tụ , các bạn có thể thử thay đổi các phương thức khác theo bài toán của bạn xem sao, biết đâu trời lại đẹp. Chúc các bạn một ngày học tập và làm việc hiệu quả. Cảm ơn và nhớ để lại cho mình một upvote và một like nhé. Thanks you!!!

References

1. https://medium.com/techspace-usict/normalization-techniques-in-deep-neural-networks-9121bf100d8#:~:text=Layer normalization normalizes input across,batch dimension in batch normalization.&text=The authors of the paper,norm in case of RNNs.
2. https://analyticsindiamag.com/understanding-normalization-methods-in-deep-learning/
3. https://arxiv.org/pdf/1502.03167.pdf
4. https://arxiv.org/pdf/1805.11604.pdf