Mô hình hồi quy ứng dụng trong bài toán dự đoán giá bất động sản - Machine Learning (phần 3)

Bài đăng này đã không được cập nhật trong 3 năm

Xin chào tất cả các bạn, chúng ta cùng khởi động một tuần mới với bài viết tiếp theo về mô hình hồi quy áp dụng trong bài toán dự đoán giá của bất động sản nhé. Trong bài viết này mình sẽ trình bày một số kĩ thuật để cải tiến mô hình hồi quy của các bạn cho hiệu năng tốt hơn các phương pháp đã áp dụng trong bài trước. OK, kiếm một tách cà phê và bắt đầu ngay thôi.

Vấn đề

Sắp có lương rồi quẩy lên anh em ơi
Xàm quá, quay lại chủ đề chính nào. Như bài trước chúng ta thấy rằng thông qua mô hình hồi quy chúng ta biểu diễn được giá của một ngôi nhà phụ thuộc như thế nào vào một số feature của nó như số phòng tắm, số phòng ngủ, năm xây dựng... Sự phụ thuộc này là phụ thuộc đơn lẻ giữa từng thuộc tính vào giá. Có nghĩa là chúng ta đang xem xét xem một thuộc tính thay đổi sẽ ảnh hưởng đến giá cả như thế nào. Tuy nhiên, mô hình này chưa tính đến trường hợp, nếu hai thuộc tính cùng thay đổi (ví dụ như diện tích và năm bán) thì ngoài việc phụ thuộc đơn lẻ giữa từng thuộc tính vào giá, thì sự kết hợp giữa hai yếu tố thay đổi này cũng ảnh hưởng đến giá không kém. Vậy làm thế nào để tìm được sự ảnh hưởng này. Chà chà...đau đầu phết đấy, nhưng không sao cả, điều gì cũng có cách giải quyết của nó... Chúng ta bắt đầu ngay thôi

Giải pháp

Xét một mô hình đơn giản ở không gian hai chiều. Ta giả sử giá của bất động sản chỉ phụ thuộc vào hai yếu tố là diện tích (***X!***) và vị trí (X2) thì hàm giá của chúng ta được biểu diễn như sau:

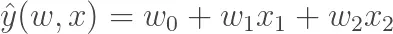
Đây là một hàm số bậc nhất với đồ thị dạng đường thẳng:

và như chúng ta đã phân tích thì sự phụ thuộc tuyến tính bậc nhất chưa biểu diễn được sự ảnh hưởng của việc kết hợp giữa các yếu tố khi các thuộc tính cùng thay đổi. Vậy nên một ý tưởng của chúng ta đó là nâng bậc cho mô hình tuyến tính. Giả sử như mô hình trên được nâng bậc thành bậc 2, chúng ta có hàm giá của bất động sản có dạng như sau:

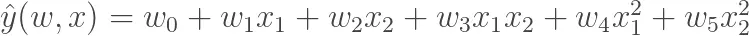
latex (1).png

Lúc này đường hồi quy chúng ta có dạng một đường cong đi qua các điểm dữ liệu:

alt

Dễ thấy mô hình này vẫn tuân theo quy luật tuyến tính với các biến

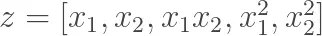
latex (2).png

và theo dõi sự ảnh hưởng kết hợp của các thuộc tính băng các hệ số bậc 2...ví dụ trong hàm giá trên là các hệ số W3, W4 và W5 đó.

Bây giờ chúng ta cùng thử chạy thử nghiệm xem. Trong bài viết này mình sẽ sử dụng PolynomialFeatures trong Scikit Learn để nâng bậc của mô hình. Và sau đó vẫn áp dụng các phương pháp đã dùng ở bài trước để so sánh hiệu quả của các phương pháp. OK các bạn đã sẵn sàng rồi phải không nào. Cùng mình bắt tay vào coding nhé.

Thử nghiệm

Chúng ta sẽ thử nghiệm phương pháp vừa nói trên bằng việc viết một hàm polynomialRegression và so sánh với mô hình ban đầu với cùng một phương pháp training cho tập dữ liệu huấn luyện là LinearRegression


def polynomialRegression(X_train, Y_train, X_test, Y_test, degree):
    poly_model = Pipeline([('poly', PolynomialFeatures(degree)),
                           ('linear', linear_model.LinearRegression(fit_intercept=False))])
    poly_model = poly_model.fit(X_train, Y_train)
    score_poly_trained = poly_model.score(X_test, Y_test)

    return score_poly_trained

Để so sánh trong hàm main chúng ta viết như sau:

if __name__ == "__main__":
    data = getData()
    if data is not None:
        # Selection few attributes
        attributes = list(
            [
                'num_bed',
                'year_built',
                'num_room',
                'num_bath',
                'living_area',
            ]
        )
        # Vector price of house
        Y = data['askprice']
        # print np.array(Y)
        # Vector attributes of house
        X = data[attributes]
        # Split data to training test and testing test
        X_train, X_test, Y_train, Y_test = train_test_split(np.array(X), np.array(Y), test_size=0.2)
        # Linear Regression Model
        linearScore = linearRegressionModel(X_train, Y_train, X_test, Y_test)
        print 'Linear Score = ' , linearScore
        # Poly Regression Model
        polyScore = polynomialRegression(X_train, Y_train, X_test, Y_test, 2)
        print 'Poly Score = ', polyScore

Ở đây chúng ta sẽ so sánh mô hình bậc hai và mô hình bậc nhất. Sau khi chạy hàm main kết quả chúng ta thu được như sau:

Connected to pydev debugger (build 162.1967.10)
-- home_data.csv found locally
Linear Score =  0.523266077498
Poly Score =  0.601673555506

Process finished with exit code 0

Chúng ta có thể thấy được hiệu quả của mô hình hồi quy có nâng bậc tốt hơn một chút so với mô hình tuyến tính đơn thuần. Tuy nhiên không có một phương pháp nào là đúng cho mọi tập dữ liệu. Phương pháp nâng bậc cho chúng ta thấy được sự ảnh hưởng của các thuộc tính kết hợp tuy nhiên nó cũng có những nhược điểm của nó, chúng ta sẽ bàn luận trong phần tiếp theo đây

Nhược điểm

Bản chất của việc nâng bậc mô hình là chuyển vector thuộc tính X từ một vector có số chiều nhỏ thành một vector có số chiều lớn hơn rất nhiều theo quy luật số mũ. Nếu số lượng dữ liệu của chúng ta nhỏ mà số chiều của vector thuộc tính lại quá lớn dẫn đến việc giải quyết bài toán hồi quy với số chiều cao và hiển nhiên là độ chính xác sẽ rất thấp. Điều đó cho chúng ta thấy cần phải sàng lọc và lựa chọn thuộc tính thật tốt trước khi đưa vào mô hình. Đây là cả một nganh khoa học mà chúng ta có thể tìm hiểu thêm tại đây. Nếu có cơ hội mình sẽ viết một bài chia sẻ riêng về Feature Engineering. Nó thật sự rất thú vị đó

Kết luận

Qua việc nâng bậc của mô hình hồi quy có thể tìm ra được sự phụ thuộc kết hợp giữa các Feature đến giá của bất động sản. Tuy nhiên nếu tập dữ liệu quá nhỏ so với số lượng Feature thì khi nâng bậc sẽ dẫn đến bài toán tối ưu với số chiều cao và làm giảm độ chính xác của mô hình. Điều đó cho thấy việc lựa chọn khéo léo các Feature là vô cùng cần thiết trước khi áp dụng bất kì mô hình nào.